Skip to content
\[ \newcommand{abs}[1]{\left|#1\right|} \]

大纲

  1. 图、曲面与复形
  2. 同调、上同调与对偶
  3. Morse函数及其应用
  4. 持续同调的计算和加速方法
  5. 持续同调的稳定性理论
  6. 持续同调的向量化
  7. Mapper及持续同调的应用

拓扑空间

定义

image-20240327215559636

如图，一个集合的一个拓扑，就是这个集合的子集的集合。

连续性

对于 \(f: X \to Y\)，如果所有开集的原象为开集，那么就称 \(f\) is a continuous mapping between \(X\) and \(Y\)。

同胚

定义：若映射 \(f:X \to Y\) 是连续双射，且逆映射 \(f^{-1}\)也连续，则称 \(f\) 是一个同胚映射 (Homeomorphism)。

相应地，称 \(X\) 与 \(Y\) 是同胚的 (Homeomorphic)。

  • 本质上，同胚就相当于：两个集合之间的开集的一一对应关系。

图论

平面图

平面图的欧拉示性数是。因为，一个含有 \(n\) 个顶点的平面图的生成树只有

  • 一个面
  • \(n\) 个点
  • \(n-1\) 条边

而每增加一条边（不与其他边相交），都一定会增加一个面。因此，\(F + V - E = 2\)​。

另外，\(E \leq 3V-6\)（可以通过【如果 \(E \geq 3\)】一个面至少有 3 条边环绕，以及一条边至多与两面相交得到）

\(K_5\) 和 \(K_{3,3}\)

对于 \(K_5\) 而言，\(10 > 3 * 5 - 6\)，因此绝对不是平面图。

对于 \(K_{3,3}\) 而言，由于是二分图，因此不存在三个点两两相连，从而三角形面不存在，也就是说 \(4F \leq 2E\)，从而必须满足 \(2V- E \geq 4\)，可惜 \(2 * 6 - 9 = 3 < 4\)，因此也不是平面图。

之后还有一个 Kuratowski 定理：一个简单图是平面图 ⇔ 它不存在与上述两图同胚的子图。

拓扑

可定向性

通俗来说，就是一个箭头平滑地绕行，能否箭头指向的方向与箭头位置无关。

  • 莫比乌斯环就是反例

连通和

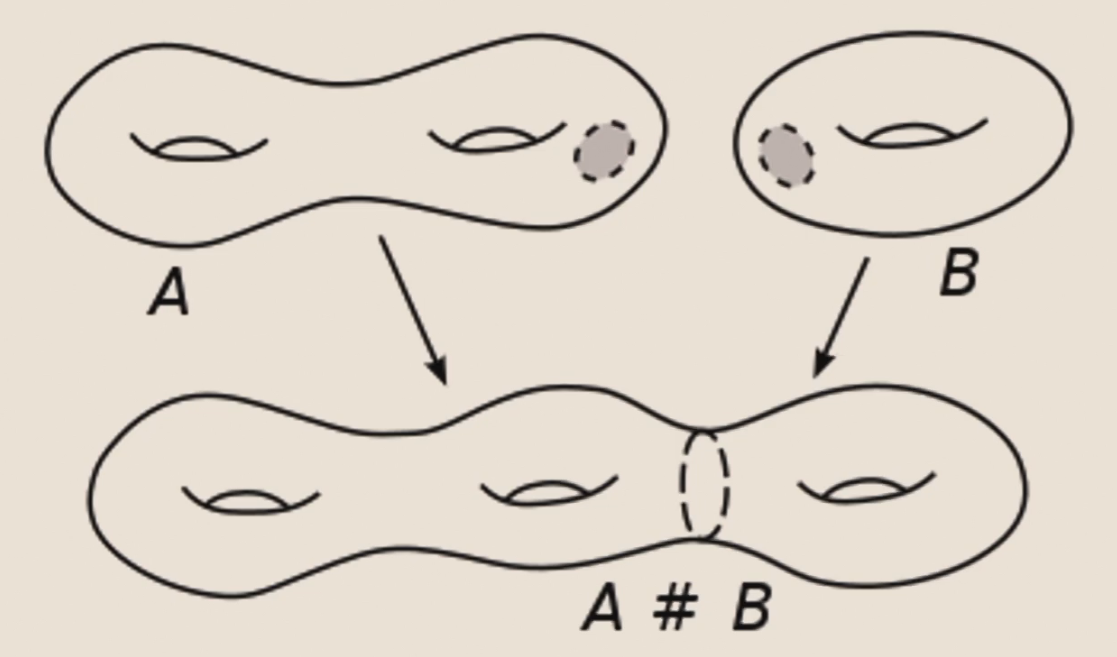
image-20240329075246942

如图，分别从 A、B 处挖去一个“开”洞，然后将两者粘在一起，就是连通和，记作 \(A \# B\)。

紧可定向 2-流形的分类

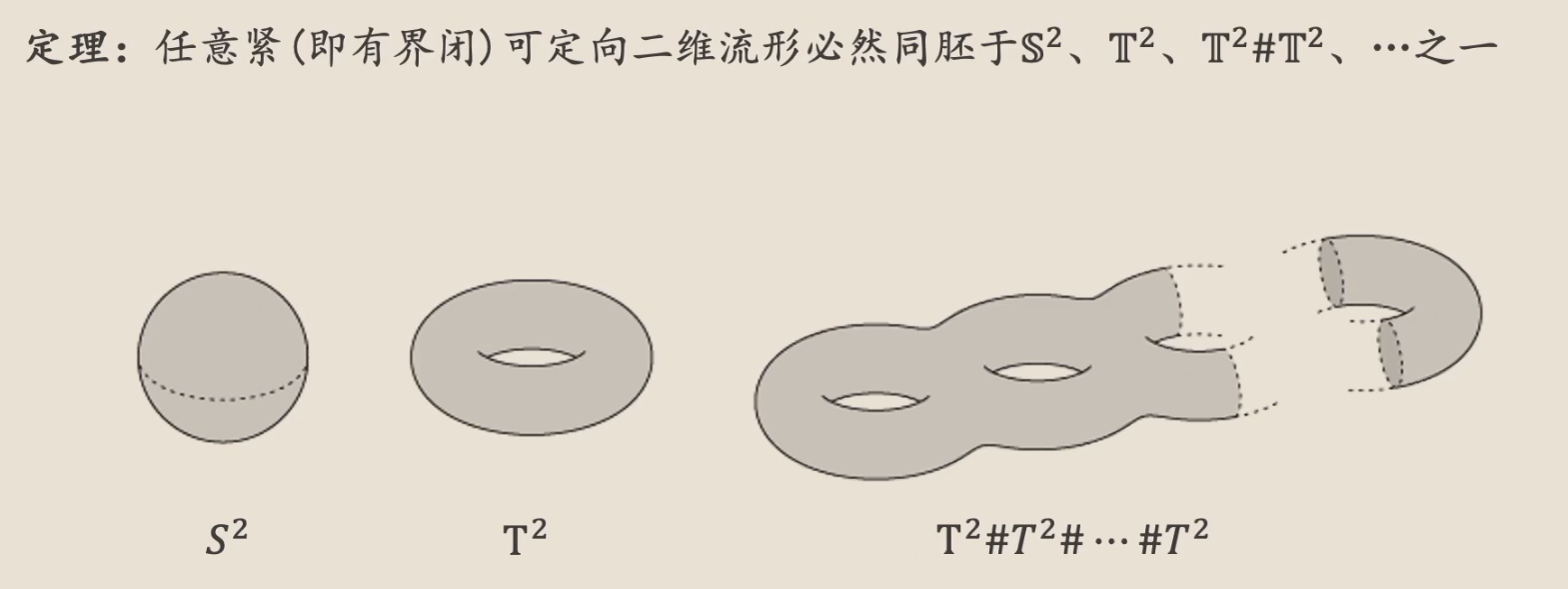
image-20240329075830813

亏格

image-20240329080227778

由于紧可定向流形必然同胚于上述的一种“标准型”，而这些标准型的亏格正好等于其“洞”的数量。

因此，对于紧可定向2-流形而言，亏格就是洞的数量。

  • 注意：亏格仅仅定义在 2-流形上，而 Betti Number 适用于所有的流形。

紧可定向 2-流形的欧拉示性数

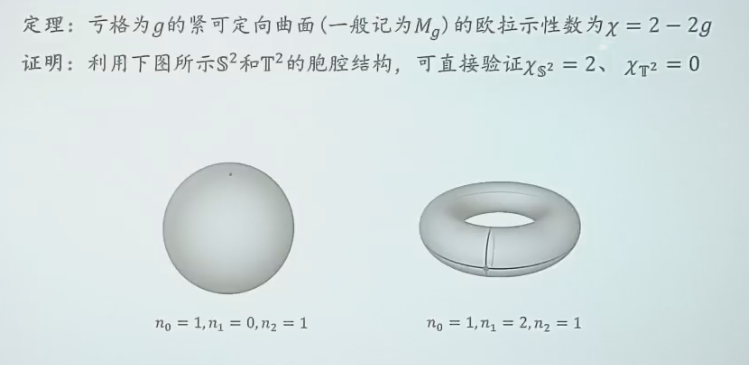
image-20240329081517419

证明也比较直观。本质上就是使用连通和进行数学归纳。

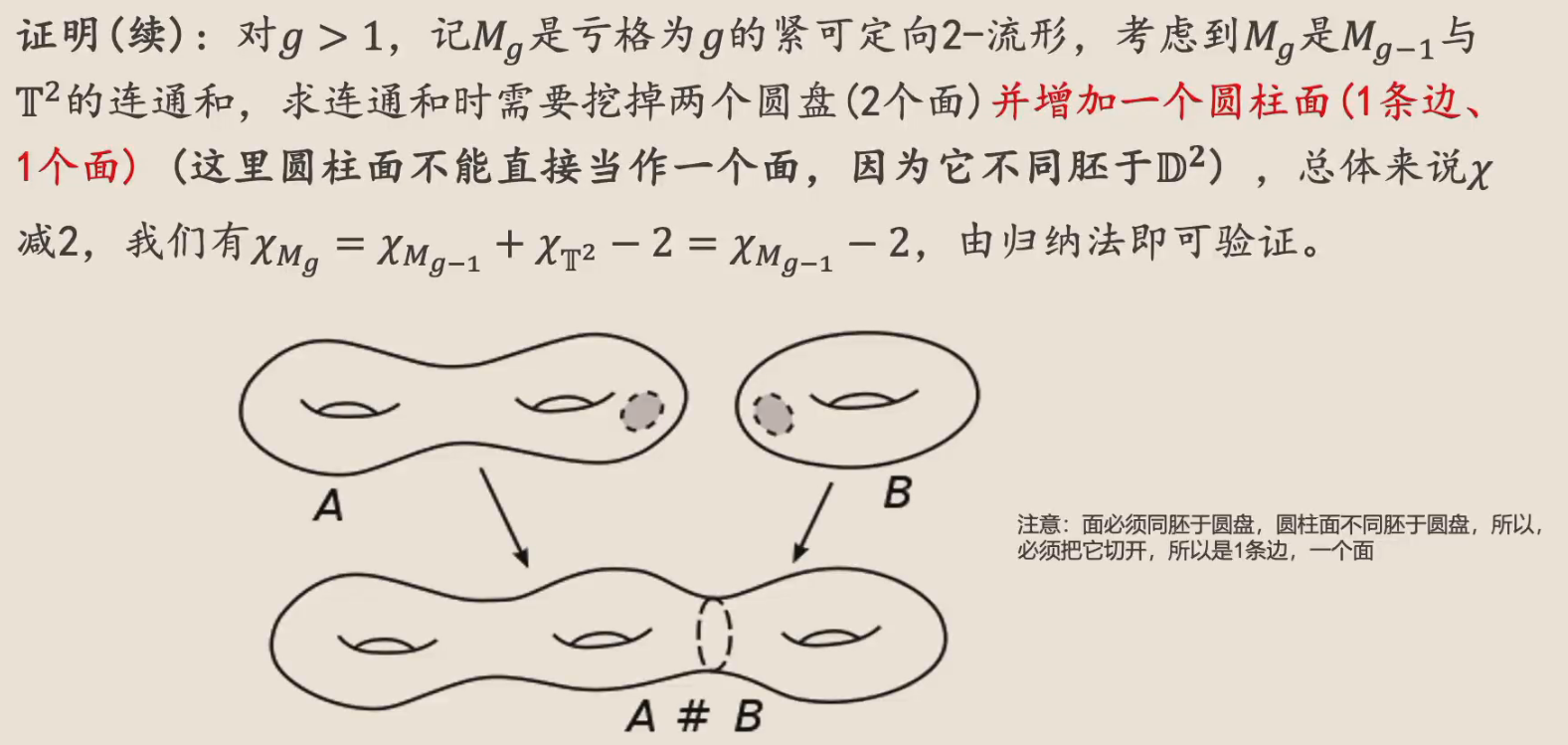
image-20240329081903499

  • 注意：\(边 \backslash 点\) 和 \(面 \backslash (边 \cup 点)\) 都必须是开集。因此圆柱面必须要有 1 条边，才能将这个圆柱面“切开”，变成一个开矩形。

例子

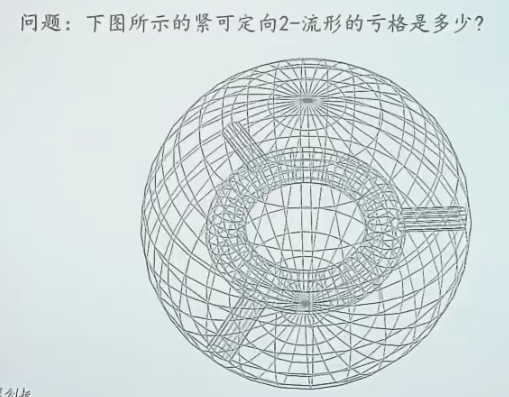
image-20240329083349651

如图，球面的示性数是 2，环面是 0。由于做了三次连通和（三个圆柱面），因此欧拉示性数是 2 + 0 + 3 * (-2) = -4，从而亏格就是 3。

紧不可定向 2-流形

交叉帽是莫比乌斯环的二维紧流形的形式，如下图所示。

img

而射影平面又是另一大紧流形。本质上就是一个球面的对称等价类：关于原点对称的点等价。亏格为 1。

克莱因瓶是一个 torus 的原点对称等价类，亏格为 2。

  • 可以想象，由于环面上关于原点对称的两个圆的点是顺时针一一对应的，因此不能把两个圆“对着”接在一起，而要“顺着”接在一起。所以必须要穿过瓶身，做成 Klein Bottle 的样子。

分类

所有紧不可定向 2-流形都与

  • 仿射面 \(\mathbb P^2 = \mathbb S^2 / \sim\)
  • 或者若干个仿射面的连通和

同胚。

image-20240331012636426

性质 3：紧不可定向 2-流形不可嵌入 \(\mathbb R^3\)，i.e. 必然存在自相交

复形

单纯形

image-20240331014929415

image-20240331014300716

总结

  • 名词：仿射凸包、仿射独立、面、余面、恰当面、边界、内部
  • 称仿射独立的k+1个点的凸包为一个k-单形(k-simplex)
    • 因此，\(k\)-单形是一个实际上是一个在 \(\mathbb R^k\) 中的点集
    • 但是，任意的 \(k\)-单形，其实构造出它的 \(k+1\) 个点的点集是唯一确定的
    • 因此，所有 \(k\)-单形和所有 \(k+1\)​ 个仿射独立的点的点集是一一对应的
  • 正因为单形和点集是一一对应的，利用点集构造出来的单形的面、余面和恰当面才是良定义的。
  • 同时，正是因为单形实际上是（无穷）点集，我们才能利用它以及它的边界来构造出它的“内部”

单纯复形（Simplicial Complex）

单纯复形就是单纯形的一个有限集（注意是以单纯形为对象的集合，而不是单纯形的点集的并集啥的【后者是底空间】）。

同时需要满足以下两个约束：

  1. \(\forall \tau \in \mathcal K: \sigma < \tau \implies \sigma \in \mathcal K\)​
    • 也就是：单纯复形必须包括哪些单纯形——每一个单纯形必须附带其所有边界
  2. \(\forall \tau_1 \neq \tau_2 \in \mathcal K: \tau_1 \cap \tau_2 \neq \emptyset \implies \tau_1 \cap \tau_2 < \tau_1, \tau_2\)
    • 也就是：单纯复形里的单纯形必须满足哪些条件——交集必须也是其边界

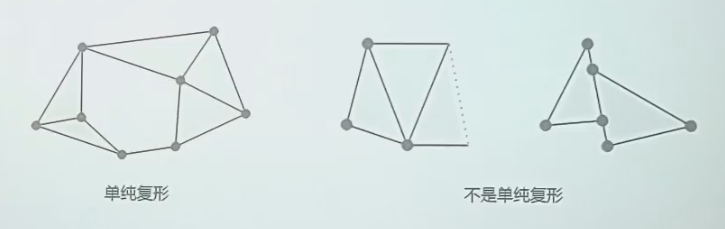
image-20240331020721218

如上图，对于“不是单纯复形”一图，

  1. 靠左的单纯复形包含了 2-单形，却没有包含作为其边界的 1-单形
  2. 靠右的单纯复形中，左右两个 2-单形的交集是中间的短线段。可惜，这条线段虽然也是 1-单形，但是不是他们俩的边界。

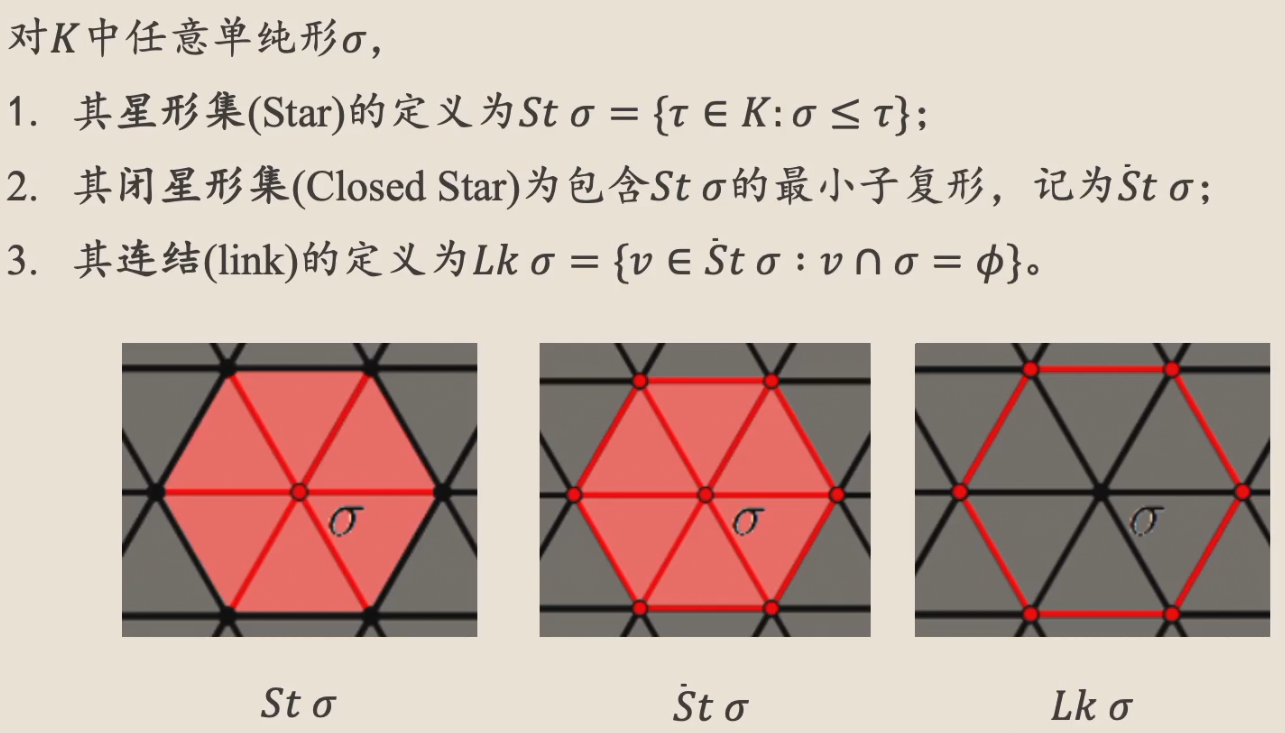
若干定义

  1. 单纯复形的维数 \(\dim \mathcal K := \max_{\sigma \in \mathcal K} \sigma\)​
  2. 底空间：\(\abs{K} = \bigcup_{\sigma \in \mathcal K} \sigma\)
    • 就是我们在一开始强调的，“单纯形的点集的并集”
  3. 如果 \(\mathcal K\) 的子集 \(\mathcal L\)​ 也满足单纯复形的条件，我们就称其为子复形
  4. 复形 \(K\) 中所有维数不超过 \(j\) 的单形组成一个特殊的子复形，称为 \(j\)-骨架 (skeleton)，记为 \(K^{(j)}\)；其中 \(K^{(0)}\) 又称为顶点集，记为 Vert K

image-20240331022158051

抽象单纯复形

image-20240331022918797

如图，抽象单纯复形，就是我们之前说的：仿射无关点集与单纯形的一一对应。

  • 但是，抽象单纯复形的点也是抽象的，i.e. 不考虑仿射相关等等问题

几何实现定理

image-20240331030633947

若干种（抽象）复形

注意： VR 复形和 Čech 复形都是抽象复形（因为我们无法保证点之间的仿射独立性）。

Čech Complex 和 VR 复形的对比

VR 复形是包含 Čech 复形的，因为：

  • VR 复形可以认为是：求集合最远点对
  • Čech 复形：求集合最小覆盖球

显然，最小覆盖球必须覆盖到最远点对，因此最小覆盖球必然比最远点对的条件更加苛刻。

因此，对于任意的点集，形成的 Čech 复形必然是 VR 复形的子复形。即：\(Cech(r) \subseteq VR(r)\)

但是，同时：\(VR(r) \subseteq Cech(\sqrt 2 r)\)

这是因为，对于任意大小为 \(d\) 的点集，如果最远点对是 \(r\)，那么，就可以形成 \(d-1\) 维单纯形（假设仿射独立）。

从而，必然被边长为最远点对距离的 \(d-1\) 维标准单纯形所包围。

由于上述的 \(d-1\) 维标准单纯性的包围超球的半径是 $$ r_d = \sqrt{\frac {d-1} d} \sqrt 2 r < \sqrt 2 r $$ \(\blacksquare\)

因此，切赫复形和 VR 复形之间，差的只是一个常数倍数，并没有本质的巨大差异。

Čech 复形的计算

Helly Theorem：如果 \(F\) 是有限个 \(\mathbb R^n\) 中的闭凸集的集合，那么：F 中所有集合的并非空，等价于 F 中任意 (d+1) 个集合的并非空。

从而：令 \(F = \set{B_x(r): x \in S}\) ，F 可以被包围在某个半径为 r 的球内部 ⇔ F 中所有集合的并非空 ⇔ F 中任意 (d+1) 个集合的并非空 ⇔ F 中任意 (d+1) 个集合可以被包围在某个半径为 r 的球内部。

image-20240331234226566

注意：下述的文字是有问题的，我还没有想清楚

上述算法，实际上应该是：\(\tau = \emptyset \lor \abs{v} = d + 1\)。（有问题）

我们可以把 \(MiniBall(\tau, v)\) 理解成：

  • \(\tau \cup v\) 是我们待包围的点（可以待在边界上，也可以不在）
  • \(v\)​ 是必须处在边界上的点

通过数学归纳法：（有问题）

  1. 最开始，\(\tau = S, v = \emptyset\)，很显然，\(\emptyset\) 一定待在边界上（空集是任何集合的子集）
  2. ……

VR 复形的计算

  1. 通过 \(\epsilon\)​ 算出邻接图
    • 从而，我们已经知道了 0 和 1 单形
  2. 从 2-单形开始，我们逐次使用 (i-1)-单形去计算 i 单形

具体方法是：

  1. 对于每一个 (i-1) 单形，找出所有满足下列要求的点
    1. 和该 (i-1) 单形的 i 个点均相邻
    2. index 小于所有 i 个点（避免重复）
      • 假设 1, 2, 3, 4 两两相邻
      • 同时，我们已经计算完了 2-单形，那么必然有 [1,2,3], [1,3,4], [1,2,4], [2,3,4]
      • 如果不加这个限制，那么就会被“找出”四次：[1,2,3] + 4, [1,3,4]+2,...
      • 如果加上这个限制，就只会被“找出”一次：[2,3,4] + 1
  2. 然后添加到 i-单形的集合中即可

Voronoi Diagram

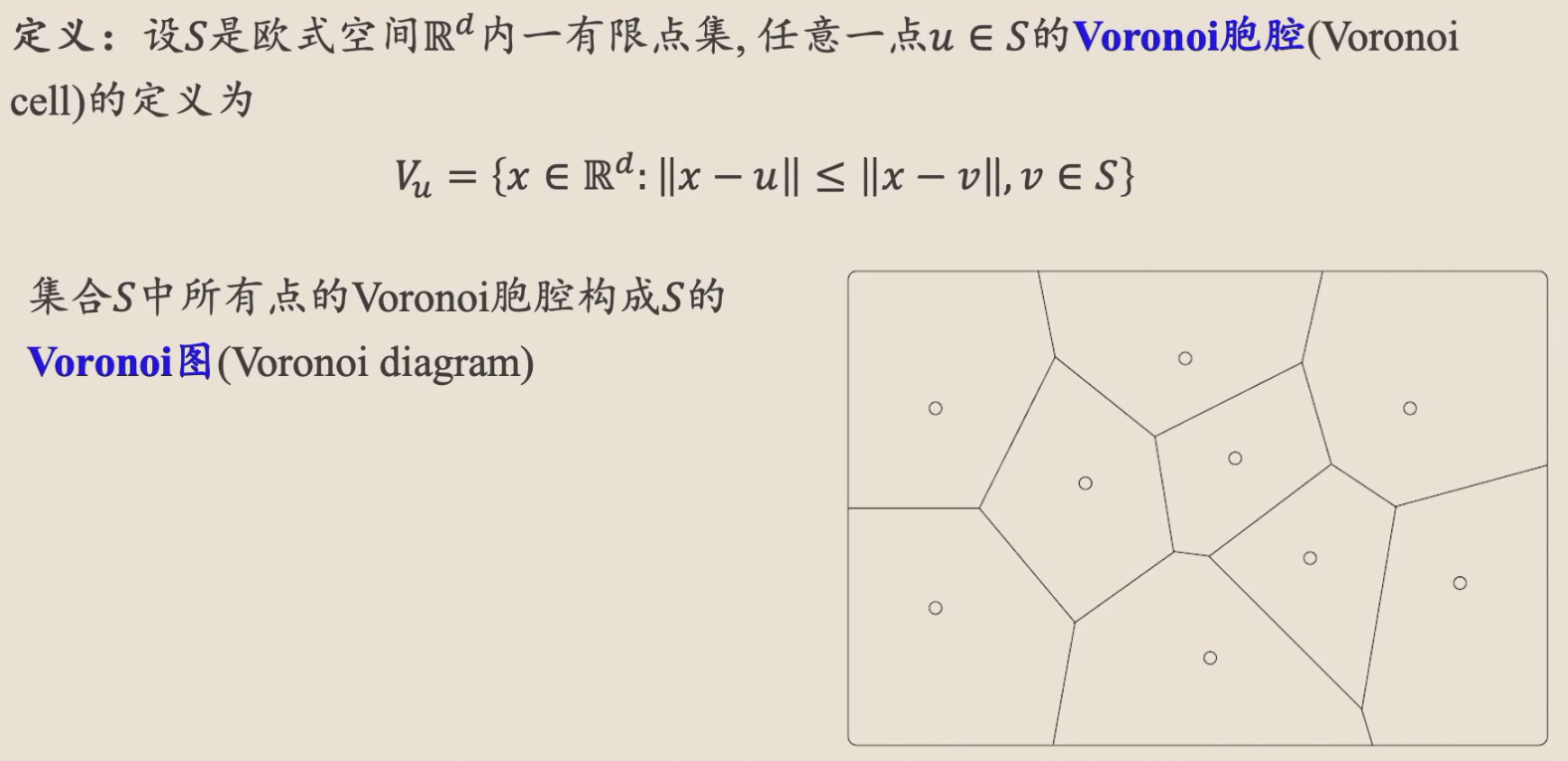
image-20240331044007632

如图，实际上，每一次 k-means （硬）聚类的时候，就会出现这种情况。

Delaunay 三角剖分 / Delaunay 复形

image-20240401010938390

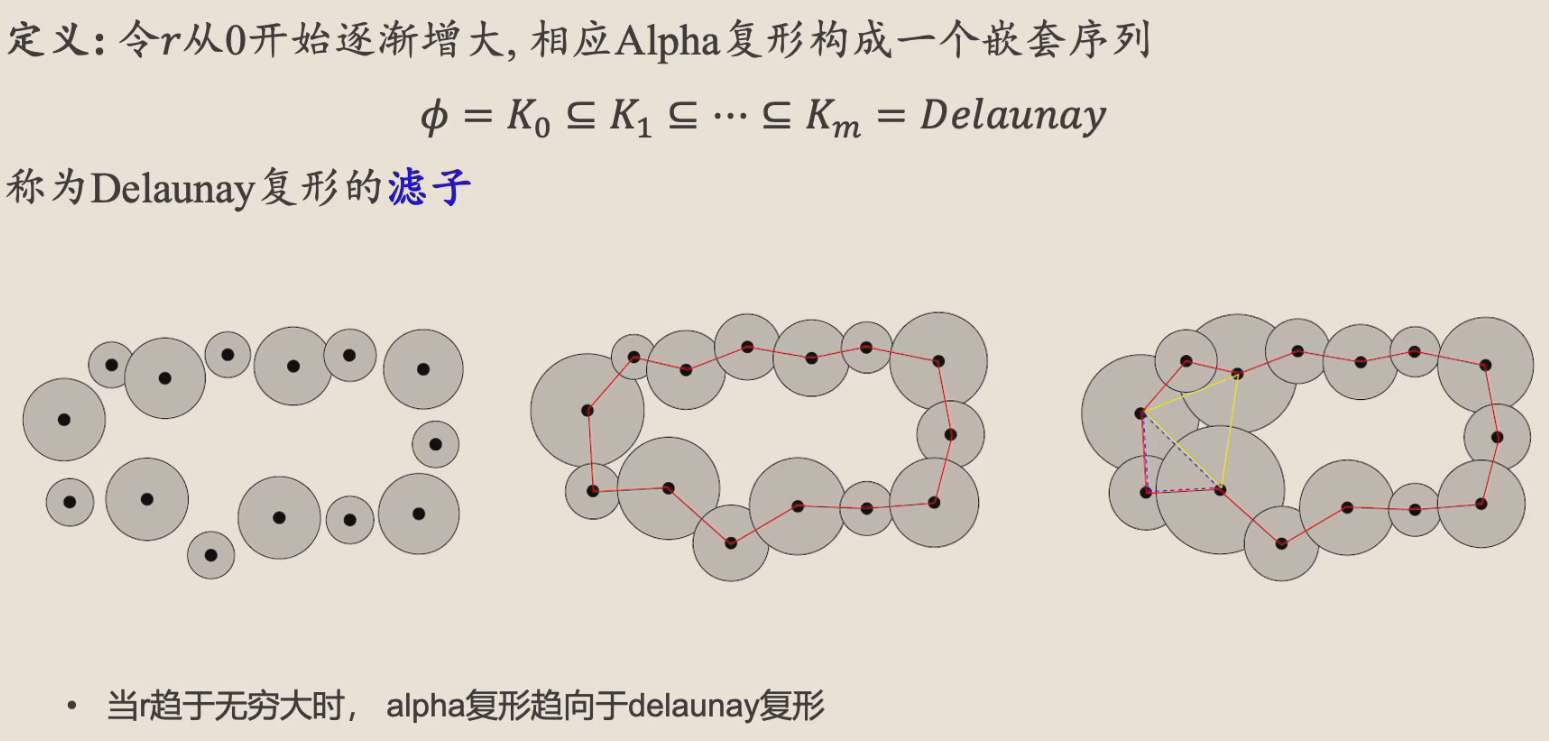
Alpha 复形

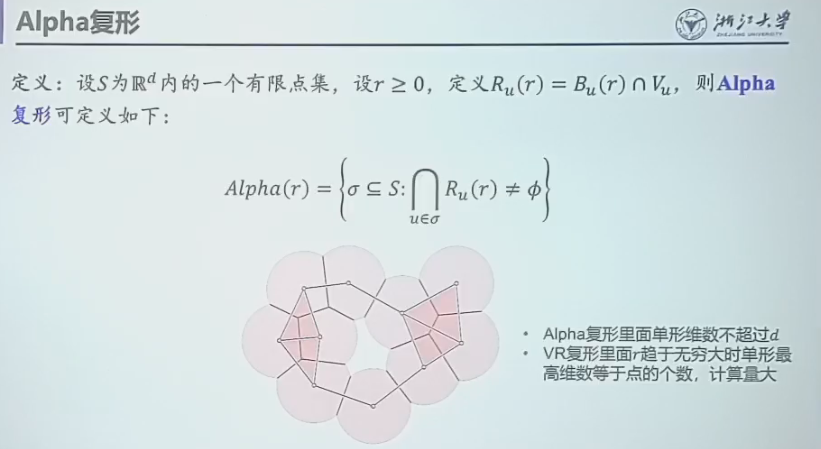
image-20240401011738037

如图，我们结合了 Delaunay 复形和 Čech 复形，也就是将 Čech 复形和 Delaunay 复形取交。从而避免了以下两个问题：

  • 由于 Delaunay 生成复形的时候没有超参数，因此无法实现持续同调
  • Čech 复形最多可能有与点数相当的维数，从而导致计算量爆炸。
    • 幸运的是，Delaunay 复形保证了单形维数不超过 d

注： 实际上，我们还可以给 Delaunay 复形进行加权，i.e. \(V_u = \set{x \in \mathbb R^d: \| x - u \| + w_u \leq \| x - v \| + w_v}\)，从而可以构造加权的 Alpha 复形。

滤子

image-20240401013355470