神经网络简介
神经网络概述
- 多层神经网络
- 每一层间的节点间都有边,边带有一个“权值”,每个点带有一个 bias
- 下一层的每个点的的 value,就是上一层的每个点分别乘以边权,再加上 下一层该点的 bias
- 每个点最终的值为 \(\sigma(value)\) (sigmoid function)
- 其中 \(\sigma(x) = \frac 1 {1 + e^{-x}}\)
- 最后,每一层的点可以由矩阵形式表示
神经网络训练
梯度下降法
对于每个特定的训练数据,input 是图片点向量,expected output 是标注数据为 1,其他均为 0 的向量。 - cost 定义为 real output 与 expected output 之差的 2-norm(自然模长) - cost 在这里认为和所有 weight 和 bias 有关
利用梯度下降法,我们每一轮改变 weight 和 bias,使得 cost 减小
对普通神经网络的分析
- 神经网络的不同层并没有去“模式识别”,边权只是一团乱麻
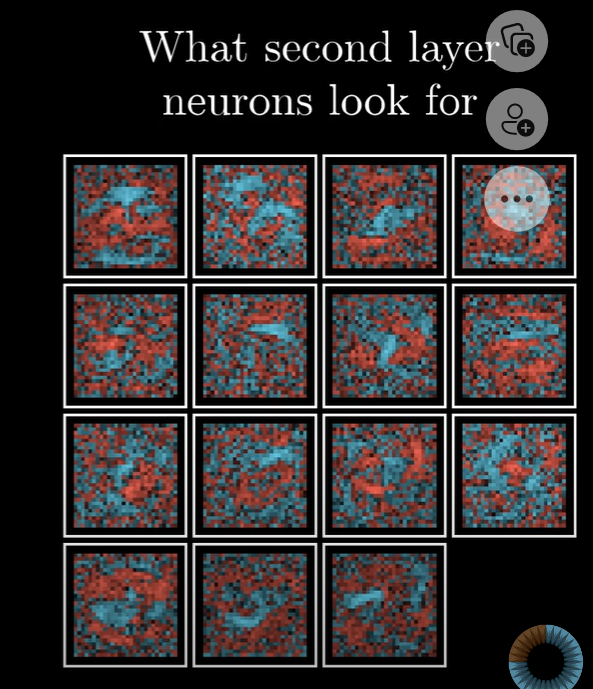
- 神经网络虽然大部分情况下,会对某个正确图片进行正确输出。但是,对于也是一团乱麻的图片,网络有时并不会给出“不确定”的信息,而是也(很有把握的)把它当成了某个数字
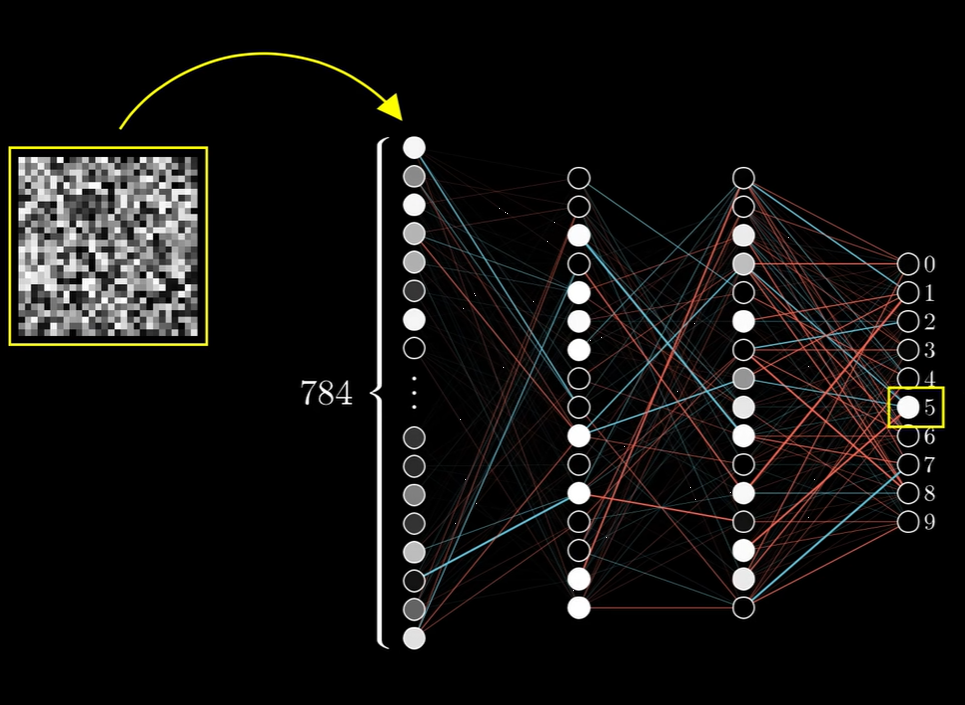
- 神经网络只能识别数字,不能重新把数字描绘出来
反向传播计算梯度
数学基础
以多层单个神经元和 \(\frac{\partial C_0}{\partial w^{(L)}}\) 为例:
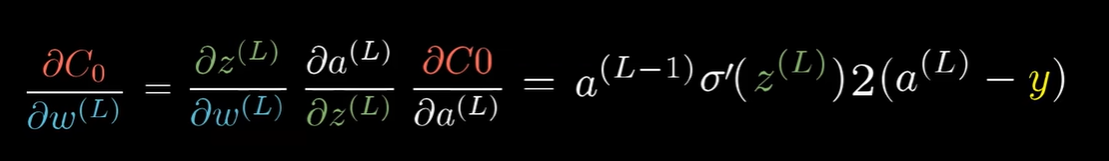
- 其中:
- \(C_0 = (\lVert a^{(L)} - y \rVert _2)^2\),也就是误差的平方和
- \(\frac{\partial C_0}{\partial b^{(L)}}, \frac{\partial C_0}{\partial a^{(L-1)}}\) 同理
- 高维(多层多个神经元)情况类似
当然,实际情况下,我们会使用所有样本(or 因性能起见,使用部分随机样本):
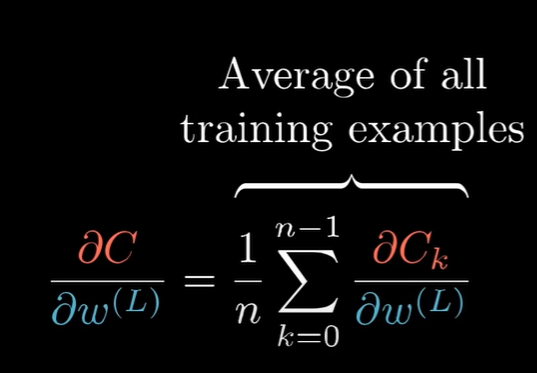
反向递归求偏导
以多层单个神经元和 \(\frac{\partial C_0}{\partial w^{(n)}}\) 为例。由链式法则:
\[
\frac{\partial C_0}{\partial w^{(n)}} = \frac{\partial C_0}{\partial a^{(L)}}(\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial a^{(L-1)}})(\frac{\partial a^{(L-1)}}{\partial z^{(L-1)}}\frac{\partial z^{(L-1)}}{\partial a^{(L-2)}})\dots(\frac{\partial a^{(n+1)}}{\partial z^{(n+1)}}\frac{\partial z^{(n+1)}}{\partial a^{(n)}})\frac{\partial a^{(n)}}{\partial z^{(n)}}\frac{\partial z^{(n)}}{\partial w^{(n)}}
\]
从而,我们对每一层由后到前地递归计算,就可以计算出 cost 关于所有边权和 bias 的偏导数,并进行梯度下降法。
补充
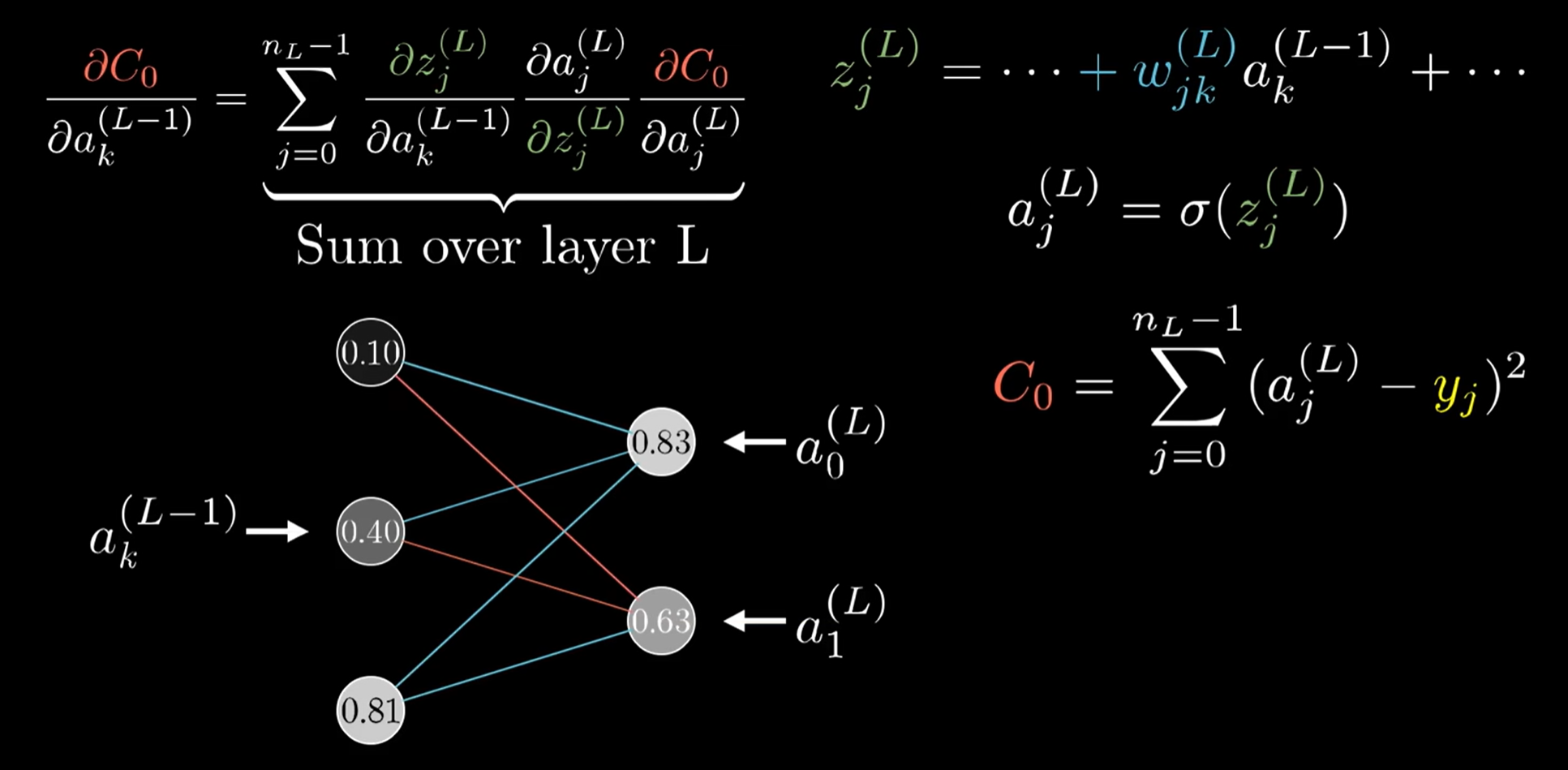
对于多层多神经元的网络,计算如下: