三

本文由简悦 SimpRead 转码，原文地址 zhuanlan.zhihu.com

在这一部分，我们开始应用我们从第 1 和第 2 部分学到的数学来计算单纯复形有趣的拓扑特征。

回到单纯同调

我们已经讨论了足够多的群论内容，能够完成我们在单纯复形上的同源群的计算。你们应该回忆一下，我们已经给出了第 $n$ 个同源群和第 $n$ 个连通数的定义。

连通数是我们的终极目标。他们很好地总结了单纯复形的拓扑性质。如果我们有一个形成单一圆形物体的单纯复形，那么 $b_0$ （第 $0$ 连通数）代表连接组件的数量（它是 $1$ ），而 $b_1$ 是 $1$ 维孔的数量（即圈），它也等于 $1$ ，但 1">$b_n, n>1$ 是高维孔，而它等于 $0$ 。

我们来看看是否可以计算一个简单三角形单纯复形的连通数。

$\mathcal T = \text{ {{a}, {b}, {c}, [a, b], [b, c], [c, a]} }$ （在下面有描述）

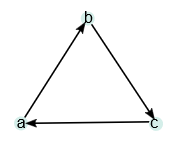
目测 $\mathcal T$ 的连通数 $b_0=1$ （ $1$ 个连接的组件）， $b_1=1$ （ $1$ 个孔），我们只计算那些连通数。

让我们慢慢地完成整个步骤。首先我们要注意 $n$ 维链。

$0$ 维链是 $0$ 维单形的集合： $\{\{a\},\{b\},\{c\}\}$ 。 $1$ 维链是 $1$ 维单形的集合： $[a, b], [b, c], [c, a]$ 。该单纯复形没有更高维的 $n$ 维链了。

现在我们可以用 $n$ 维链定义链群。我们准备用 $\mathbb Z_2$ 的系数， $\mathbb Z_2$ 是一个只有两个元素 $\{0,1\}$ 的域，其中 $1+1=0$ 。

$0$ 维链群被定义成： $\\ C_0 = \{\{x*(a,0,0)\}, \{y*(0,b,0)\}, \{z*(0,0,c)\} \mid x,y,z \in \mathbb Z_2\}$

这个群只定义了加法运算，但我们在 $\mathbb Z_2$ 中用乘法构建了这个群。因此这个群与 $\mathbb Z_{2}^{3} = Z_{2} \oplus Z_{2} \oplus Z_{2}$ 同构。

但我们也想把链群表示成向量空间。这意味着它成为一种结构，这个结构中的元素可以通过域中的元素放大或缩小 (即乘法运算)，并加在一起，所有的结果仍然在结构中。如果我们只关注加法运算，那么我们看到的是群结构，但如果我们关注加法和乘法运算，那么我们可以把它看作向量空间。

0 维链向量空间通过以下方法生成：

\[\\ \mathscr C_0 = \{\{x*(a,0,0)\}, \{y*(0,b,0)\}, \{z*(0,0,c)\} \mid x,y,z \in \mathbb Z_2\} \\\]

（是的，它和上面的群是相同的集合）

向量空间是集合的一组元素，我们可以乘上 $0$ 或 $1$ ，然后把它们加起来。例如： $1*(a,0,0) + 1*(0,0,c) = (a,0,c)$ ，这个向量空间非常小（ $2^3=8$ 个元素），我们可以列出所有的元素。他们是：

$\\ \mathscr{C_0} = \begin{Bmatrix} (a,0,0), (0,b,0), (0,0,c), (a,b,0) \\ (a,b,c), (0,b,c), (a,0,c), (0,0,0) \end{Bmatrix}$

你可以看到，我们可以在这个向量空间中添加任何两个元素，结果将是向量空间中的另一个元素。随便举个例子： $(a,0,c) + (a,b,c) = (a+a,0+b,c+c) = (0,b,0)$ 。加法是分量方式的。我们也可以用向量乘以一个域 $\mathbb Z_2$ 中的元素，但因为我们的域只有两个元素，结果比较无聊，只有 $1*(a,b,0) = (a,b,0)$ 和 $0*(a,b,0) = (0,0,0)$ ，但乘法运算仍然会在我们的向量空间中产生一个元素。

我们可以把这个向量空间表示为一个多项式，那么我们的 0 维链向量空间能等价地定义为：

$\\ \mathscr{C_0} = \{xa + yb + zc \mid z,y,z \in \mathbb Z_2\}$

我们可以很容易地把一个多项式 $a+b+c$ 翻译成它的有序集符号 $(a,b,c)$ ，或者 $a+b$ 是 $(a,b,0)$ 。作为多项式集合的向量空间是这样的： $\\ \mathscr{C_0} = \begin{Bmatrix} \text{ {0}, {a}, {b}, {c}, {a+b}, {b+c}, {a+c}, {a+b+c}} \end{Bmatrix}$

一般来说，使用多项式形式更方便，因为我们可以做一些熟悉的代数方程, 像这样： $a+b=0 \\a = -b \\a = b$

（记得 $\mathbb Z_2$ 中的一个元素的逆是它自己，即 $-b=b$ ，其中 “ $-$ ” 表示负）。

注意：知道我们讨论的是群体还是向量空间是非常重要的。我将用普通的 $C$ 代表链群而花体 $\mathscr C$ 代表链（向量）空间。它们具有相同的底层集，只是定义了不同的操作。如果我们讨论群形式，我们只能参考它的加法运算，而如果我们讨论向量空间形式，我们可以讨论它的乘法运算和加法运算。

我们对 1 维链进行相同的操作： $[a, b], [b, c], [c, a]$ 。我们可以用 $1$ 维链集定义另一个链群， $C_1$ 。它将与 $C_0$ 和 $\mathbb Z_{2}^{3}$ 同构。 $C_1 = \{\ (\ x([a, b]), y([b, c]), z([c, a])\ ) \mid x,y,z \in \mathbb Z_2\ \}$ 我们可以用和定义 $C_0$ 同样的方法来使用这个链定义向量空间 $\mathscr C_1$ 。我将使用多项式形式。记住，链群和向量空间有相同的集合，只是向量空间有两个二进制运算而不是一个。这是向量空间中元素的完整列表：

\[\\ \mathscr{C_1} = \begin{Bmatrix} \text{ {[a, b]}, {[b, c]}, {[c, a]}, {[a, b] + [b, c]}, {[b, c] + [c, a]}, {[a, b] + [c, a]}, {[a, b] + [b, c] + [c, a]}, {0} } \end{Bmatrix} \\\]

为了澄清边界图，这里有一个图。这说明了边界操作符如何映射 $C_0$ 的每个元素到 $C_1$ 的元素。

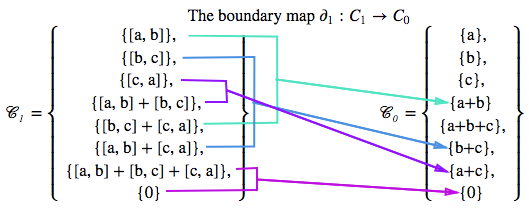
现在我们可以开始计算第一个连通数， $b_0$ 。

回想一下连通数的定义：

第 $n$ 个连通数 $b_n$ 定义为 $H_n$ 的维度， $b_n = dim(H_n)$ 。

再回忆一下同调群的定义：

第 $n$ 个同调群 $H_n$ 定义为 $H_n=Ker\partial_n/Im\partial_{n+1}$ 。

最后，回顾一下内核的定义：

$\partial(C_n)$ 的核（记作 $Ker(\partial(C_n))$ ）是 $n$ 链 $Z_n \subseteq C_n$ 的群，其中 $\partial(Z_n) = 0$ 。

首先，我们需要边界 $C_0$ 的核 $Ker\partial(C_0)$ 。记得边界映射 $\partial$ 为我们提供了 $C_n \rightarrow C_{n-1}$ 的映射。

在所有情况下，边界的 $0$ 维链是 $0$ ，因此 $Ker\partial(C_0)$ 是整个 $0$ 维链。 $Ker\partial(C_0) = \{a, b, c\}$ 这形成了另一个 $0$ 圈的群，记为 $Z_0$ （或者 $Z_n$ ）， $Z_0$ 是 $C_0$ 的子群，即 $Z_n \leq C_n$ 。加上 $Z_2$ 的定义， $Z_0$ 也与 $Z_2$ 同构，因此它和 $C_0$ 一样。

另一件事是我们需要找到同调群 $H_0$ 的 $Im\partial_{1}$ 。这形成了 $Z_0$ 的子群，记作 $B_0$ ，它是 $(n+1)$ 维链的边界的群。因此 $B_n \leq Z_n \leq C_n$ 。 $\partial{C_1} = \partial({[a, b], [b, c], [c, a]} = (a + b) + (b + c) + (c + a) \\ \partial{C_1} = (a + b) + (b + c) + (c + a) = (a + a) + (b + b) + (c + c) = (0) + (0) + (0) = 0 \\ \partial{C_1} = 0$

所以 $Im\partial_{1} = 0$ 。

因此我们计算子群 $H_0 = Z_0\ /\ B_0$ ，这种情况下： $Z_0 = \text { { {a, b, c}, {0} } } \\ B_0 = \{0\}$

所以我们用 $Z_0$ 中两个元素中的 $\{0\}$ 的左陪集来得到商群： $\\ Z_0\ /\ B_0 = \text { { {a, b, c}, {0} } } = Z_0$

总之，如果 $B_n = \{0\}$ ，那么 $Z_n\ /\ B_n = Z_n$ ，所以 $H_0 = Z_0$ 。

连通数 $b_0$ 是 $H_0 = Z_0$ 的维度。什么是 $H_0$ 的维度？它有两个元素，但是维度被定义为一个群中最小的生成元集合，因为这个群与 $Z_2$ 同构，所以它只有 $1$ 个生成元。因为整个群可以通过反复加 $1$ 来形成，即 $1+1=0, 1+1+1 = 1$ ，然后我们就能得到整个 $Z_2$ ，所以 $Z_2$ 的生成元是 $1$ 。

所以 $b_0 = dim(H_0) = 1$ ，这就是我们所期望的，这个单纯复形有 $1$ 个相连的分量。

现在开始计算 $1$ 维连通 $b_1$ 。这次它可能会有些不同，因为计算 $\text{Ker}\partial(C_1)$ 将变得更复杂。我们需要做一些代数运算。

所以，第一，我们需要 $Z_1$ ， $1$ 维圈的群。这是边界为 $0$ 的 $1$ 维单形的集合。记得 $1$ 维链是 $\{ [a,b], [b,c], [c,a]\}$ ，而当它应用在 $Z_1$ 上，它形成了 $1$ 维链群 $C_1$ 。我们将构建这样一个等式：

其中，这是向量空间中任何元素的一般形式然后取边界提出因数

\[\\ \mathscr C_1 = \lambda_0([a,b]) + \lambda_1([b,c]) \lambda_2([c,a]) \text{ ... 其中 $\lambda_n \in \mathbb Z_2$，这是向量空间$\mathscr C_1$中任何元素的一般形式 } \\ \lambda_0([a,b]) + \lambda_1([b,c]) + \lambda_2([c,a]) = 0 \text{ ... 然后取边界} \\ \partial(\lambda_0([a,b]) + \lambda_1([b,c]) + \lambda_2([c,a])) = 0 \\ \lambda_0(a+b) + \lambda_1(b+c) + \lambda_2(c+a) = 0 \\ \lambda_0{a} + \lambda_0{b} + \lambda_1{b} + \lambda_1{c} + \lambda_2{c} + \lambda_2{a} = 0 \\ a(\lambda_0 + \lambda_2) + b(\lambda_0 + \lambda_1) + c(\lambda_1 + \lambda_2) = 0 \text{ ...提出因数 a,b,c} \\\]

满足这个方程后，需要把每一项的所有系数 $\lambda_n$ 加起来等于 $0$ ，来让 $a,b,c$ 变成 $0$ 。也就是说，如果整个等式等于 $0$ ，那么每一项都等于 $0$ ，如 $a(\lambda_0 + \lambda_2) = 0$ ，因此 $\lambda_0 + \lambda_2 = 0$ 。现在我们有了一个线性方程组：

得出$\lambda_0 + \lambda_2 = 0 \\ \lambda_0 + \lambda_1 = 0 \\ \lambda_1 + \lambda_2 = 0 \\ \text{...得出...} \\ \lambda_0 = \lambda_2 \\ \lambda_0 = \lambda_1 \\ \lambda_1 = \lambda_1 \\ \lambda_0 = \lambda_1 = \lambda_2$

对于上面的方程，所有的系数都是相等的。我们用一个符号替换所有的 $\lambda$ ，即 $\lambda_0, \lambda_1, \lambda_2 = \phi$ 。

现在，让我们回到 1 维链向量空间的一般表达式 $\mathscr C_1 = \lambda_0([a,b]) + \lambda_1([b,c]) + \lambda_2([c,a])$ 。当我们把它的边界设为 $0$ 时，我们会得到 $\lambda_0 = \lambda_1 = \lambda_2$ ，而我建议我们用符号 $\phi$ 代替。

因此，循环群：

记住来自，所以它是或。$\\ Z_1 \leq \mathscr C_1 = \phi([a,b]) + \phi([b,c]) + \phi([c,a]) \\ Z_1 = \phi([a,b] + [b,c] + [c,a]), \text{ ...记住 \(\phi$ 来自 $\mathbb Z_2$，所以它是0或1。}\)

因此循环群只包含两个元素，它和 $Z_2$ 同构。

我会引入新的符号。如果数学结构 $G_1,G_2$ 同构，那么我们记作 $G_1 \cong G_2$ 。

如果 $\phi = 0$ ，那么 $\phi([a,b] + [b,c] + [c,a]) = 0([a,b] + [b,c] + [c,a]) = 0$ ，但如果 $\phi = 1$ ，那么 $\phi([a,b] + [b,c] + [c,a]) = 1([a,b] + [b,c] + [c,a]) = [a,b] + [b,c] + [c,a]$ ，所以整个群是： $\\ Z_1 = \begin{Bmatrix} [a,b] + [b,c] + [c,a] \\ 0 \end{Bmatrix}$

边界群 $B_1 = Im\partial(C_2)$ ，但因为 $C_2$ 是空集，所以 $B_1 = \{0\}$ 。

我们可以再次计算出同源群： $\\H_1 = Z_1 / B_1 = \begin{Bmatrix} [a,b] + [b,c] + [c,a] \\ 0 \end{Bmatrix}$

而连通数 $b_1 = dim(H_1) = 1$ ，因为在群 $H_1$ 中，我们只有一个生成元。

所以这就是非常简单的单纯复形。我们将转到一个更大的复形。这次我将不会详细介绍，并将使用许多我已经定义或描述过的简化符号和约定俗成。

让我们来完成和之前差不多，但更复杂的单纯复形： $\\ S = \text{{[a], [b], [c], [d], [a, b], [b, c], [c, a], [c, d], [d, b], [a, b, c]}}$

（下面是描述）

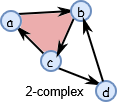
注意现在我们有一个 $2$ 维单形 $[a,b,c]$ ，被描绘成实心三角形。

这次我们用整个整数域 $\mathbb Z$ 作为我们的系数，所以由此产生的向量空间将是无限的，而不是我们可以列出的有限空间。既然我们用了 $\mathbb Z$ ，我们就必须定义 “负” 单形是什么意思，即 $-[c,a]$ 的意义？我们之前讨论过了，基本上，我们定义了两种方法，一个单纯形可以被定向，而对原定义的相反方向则被赋予一个单纯形的 “负” 值。

所以 $[a,c] = -[c,a]$ 。但 $[a,b,c]$ 呢？有两种方法来排列 $3$ 个元素列表，但它只有两个方向。

如果你见过以前的定向单形:

这只有两种方法可以 “围绕” 循环，顺时针或者逆时针。

$[a,b,c]$ 是顺时针。

$[c,a,b]$ 也是顺时针。

$[a,c,b]$ 是逆时针，所以 $[a,b,c] = [c,a,b] = -[a,c,b] = -[b,c,a]$ 。

让我们从列出我们的链组开始。

\[\\C_0 = \langle{a,b,c,d}\rangle \cong \mathbb Z^4 \\ C_1 = \langle{[a, b], [b, c], [c, a], [c, d], [d, b]}\rangle \cong \mathbb Z^5 \\ C_2 = \langle{[a, b, c]}\rangle \cong \mathbb Z \\\]

回想一下方括号的含义，这显然比我们在最后一个例子中构建群的方式要简单得多。注意每个群都与向量空间 $\mathbb Z^n$ 同构，其中 $n$ 是 $n$ 维链中单形的数量。

我们可以这样描述我们的链结构： $\\ C_2 \stackrel{\partial_1}\rightarrow C_1 \stackrel{\partial_0}\rightarrow C_0$

我们知道，我们可以很轻易地将这个单纯复形可视化，因为它有一个连接组件和一个 1 维循环（一个 1 维孔）。因此，连通数，$b_0 = 1， b_1 = 1$ ，但我们需要自己计算。

让我们从高维链群开始，即 $2$ 维链群。

记住， $Z_n = \text{Ker}\partial(C_n)$ $n$ 维循环的群，它是 $C_n$ 的子群。而 $B_n = \text{Im}\partial(C_{n+1})$ 是 $n$ 维边界的群，它是 $n$ 维循环的子集。因此 $B_n \leq Z_n \leq C_n$ 。还记得同调群 $H_n = Z_n\ /\ B_n$ 而第 $n$ 个连通数是 $n$ 维同调群的维度。

为了得到 $Z_n$ ，我们需要为 $C_n$ 中的一般元素设置表达式。让它等于以得到核只有一个解，所以所以中没有一个元素等于，因此核中只有

\[\\ \begin{aligned} C_2 &= \lambda_0{[a,b,c]}, \lambda_0 \in \mathbb{Z} \\ Z_2 &= \text{Ker}\partial{(C_2)} \\ \partial{(C_2)} &= \lambda_0{([b,c])} - \lambda_0{([a,c])} + \lambda_0{([a,b])} \text{ ...让它等于0以得到核} \\ \lambda_0{([b,c])} - \lambda_0{([a,c])} + \lambda_0{([a,b])} &= 0 \\ \lambda_0{([b,c] - [a,c] + [a,b])} &= 0 \\ \lambda_0 &= 0 \text{ ... $\lambda_0 = 0$只有一个解，所以 $0=0$. } \\ \lambda_0{[a,b,c]} &= 0, \lambda_0 = 0 \text{ ... 所以$C_2$中没有一个元素等于0，因此核中只有{0}} \\ ... \\ \text{Ker}\partial{(C_2)} &= \{0\} \\ \end{aligned}\\\]

因为没有 $3$ 维单形或更高， $B_2 = {0}$ 。因此连通数 $b_2 = dim(\{0\} / \{0\}) = 0$ 。这就是我们所期望的，单纯复形里没有 $2$ 维洞。

让我们用同样的方法处理 $C_1$ 。

让它等于以得到核现在我们可以建立一个线性方程组解方程，把答案放回表达式中指出

\[\\ \begin{aligned} C_1 &= \lambda_0[a, b] + \lambda_1[b, c] + \lambda_2[c, a] + \lambda_3[c, d] + \lambda_4[d, b], \lambda_n \in \mathbb{Z} \\ Z_1 &= \text{Ker}\partial{(C_1)} \\ \partial{(C_1)} &= \lambda_0{(a - b)} + \lambda_1{(b - c)} + \lambda_2{(c - a)} + \lambda_3{(c - d)} + \lambda_4{(d - b)} \\ \text{ ...让它等于0以得到核} \\ \lambda_0{(a - b)} + \lambda_1{(b - c)} + \lambda_2{(c - a)} + \lambda_3{(c - d)} + \lambda_4{(d - b)} &= 0 \\ \lambda_0a - \lambda_0b + \lambda_1b - \lambda_1c + \lambda_2c - \lambda_2a + \lambda_3c - \lambda_3d + \lambda_4d - \lambda_4b &= 0 \text { ...指出 a,b,c,d}\\ a(\lambda_0 - \lambda_2) + b(\lambda_1 - \lambda_0 - \lambda_4) + c(\lambda_2 - \lambda_1 + \lambda_3) + d(\lambda_4 - \lambda_3) &= 0 \\ \text{现在我们可以建立一个线性方程组...} \\ \lambda_0 - \lambda_2 &= 0 \\ \lambda_1 - \lambda_0 - \lambda_4 &= 0 \\ \lambda_2 - \lambda_1 + \lambda_3 &= 0 \\ \lambda_4 - \lambda_3 &= 0 \\ \text{解方程，把答案放回$C_1$表达式中...} \\ \lambda_0([a,b] + [b,c] + [c,a]) + \lambda_3([b,c] + \cancel{[a,c]} + [c,d] + \cancel{[c,a]} + [d,b]) &= \text{Ker}\partial{(C_1)} \\ \text{Ker}\partial{(C_1)} &= \lambda_0([a,b] + [b,c] + [c,a]) + \lambda_3([b,c] + [c,d] + [d,b]) \\ Z_1 = \text{Ker}\partial{(C_1)} &\cong \mathbb Z^2 \end{aligned}\\\]

现在开始求边界 $B_1 = Im\partial(C_2)$ 。

记住$\\ \begin{aligned} \partial(C_2) &= \lambda_0{([b,c])} - \lambda_0{([a,c])} + \lambda_0{([a,b])} \text {... 记住 \(-[a,c] = [c,a]$ ...} \\ \partial(C_2) &= \lambda_0{([b,c] + [c,a] + [a,b])} \\ B_1 = Im\partial(C_2) &= \{\lambda_0{([b,c] + [c,a] + [a,b])}\}, \lambda_0 \in \mathbb Z \\ B_1 &\cong Z \\ H_1 = Z_1\ /\ B_1 &= \{\lambda_0([a,b] + [b,c] + [c,a]) + \lambda_3([b,c] + [c,d] + [d,b])\}\ /\ \{\lambda_0{([b,c] + [c,a] + [a,b])}\} \\ H_1 &= \{\lambda_3([b,c] + [c,d] + [d,b])\} \cong \mathbb Z \end{aligned}\)

另一种更容易计算出商群 $H_1 = Z_1\ /\ B_1$ 的方法是注意 $Z_n, B_n$ 和 $\mathbb Z^n$ 中的什么同构。在这种情况下：

$\\Z_1 \cong \mathbb Z^2 \\ B_1 \cong \mathbb Z^1 \\ H_1 = \mathbb Z^2\ /\ \mathbb Z = \mathbb Z$

所以因为 $H_1 \cong \mathbb Z$ ， $H_1$ 的连通数是 $1$ ，因为 $\mathbb Z$ 的维度是 $1$ （它只有一个生成元）。

我想你们现在已经明白了，我不打算讲所有计算连通数 $b_0$ 的细节了，它应该是 $1$ ，因为只有一个连接的分量。

预告

我们已经掌握了如何手工计算简单的单纯复形的同调群和连通数。但是我们需要开发一些新的工具，这样我们就可以让计算机算法来处理一些真实的，通常更大的单纯复形的计算。下一节我们将会看到线性代数是如何为我们提供一种有效的方法的。

参考文献（网站）

参考文献（学术刊物）

Basher, M. (2012). On the Folding of Finite Topological Space. International Mathematical Forum, 7(15), 745–752. Retrieved from http://www.m-hikari.com/imf/imf-2012/13-16-2012/basherIMF13-16-2012.pdf
Day, M. (2012). Notes on Cayley Graphs for Math 5123 Cayley graphs, 1–6.
Doktorova, M. (2012). CONSTRUCTING SIMPLICIAL COMPLEXES OVER by, (June).
Edelsbrunner, H. (2006). IV.1 Homology. Computational Topology, 81–87. Retrieved from Computational Topology
Erickson, J. (1908). Homology. Computational Topology, 1–11.
Evan Chen. (2016). An Infinitely Large Napkin.
Grigor’yan, A., Muranov, Y. V., & Yau, S. T. (2014). Graphs associated with simplicial complexes. Homology, Homotopy and Applications, 16(1), 295–311. HHA 16 (2014) No. 1 Article 16
Kaczynski, T., Mischaikow, K., & Mrozek, M. (2003). Computing homology. Homology, Homotopy and Applications, 5(2), 233–256. HHA 5 (2003) No. 2 Article 8
Kerber, M. (2016). Persistent Homology – State of the art and challenges 1 Motivation for multi-scale topology. Internat. Math. Nachrichten Nr, 231(231), 15–33.
Khoury, M. (n.d.). Lecture 6 : Introduction to Simplicial Homology Topics in Computational Topology : An Algorithmic View, 1–6.
Kraft, R. (2016). Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology.
Lakshmivarahan, S., & Sivakumar, L. (2016). Cayley Graphs, (1), 1–9.
Liu, X., Xie, Z., & Yi, D. (2012). A fast algorithm for constructing topological structure in large data. Homology, Homotopy and Applications, 14(1), 221–238. HHA 14 (2012) No. 1 Article 11
Naik, V. (2006). Group theory : a first journey, 1–21.
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. (2015). A roadmap for the computation of persistent homology. Preprint ArXiv, (June), 17. Retrieved from [1506.08903] A roadmap for the computation of persistent homology
Semester, A. (2017). § 4 . Simplicial Complexes and Simplicial Homology, 1–13.
Singh, G. (2007). Algorithms for Topological Analysis of Data, (November).
Zomorodian, A. (2009). Computational Topology Notes. Advances in Discrete and Computational Geometry, 2, 109–143. Retrieved from CiteSeerX - Computational Topology
Zomorodian, A. (2010). Fast construction of the Vietoris-Rips complex. Computers and Graphics (Pergamon), 34(3), 263–271. Redirecting
Symmetry and Group Theory 1. (2016), 1–18. Redirecting