Skip to content

Overview of Data Flow Analysis

我们关心的就是 how data flows through CFG?

具体地，是 how

  • application specific data

flows through

  • nodes (i.e. basic blocks) and
  • edges (i.e. control flow)

of the CFG (i.e. the program)

绝大多数分析，都是 over-approximation: what you output may be true, and if it's true, you should (nearly) always output.

  • 又称为 may analysis

但是，还有一种分析，是 under-approximation: what you output must be true, and you don't have to output all true information.

  • 又称为 must analysis

两者 analysis，都是为了保证结果在一定层面上的可靠性。

例子

对于符号分析：

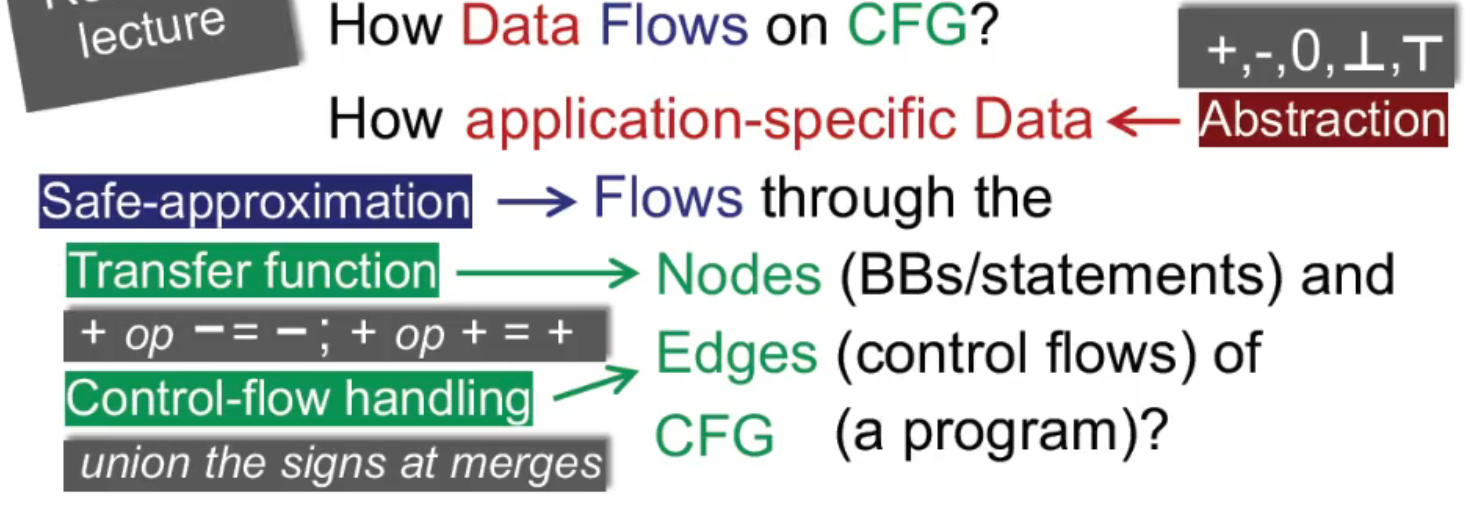
image-20240321114900045

因此，不同的 data flow analysis 有

  • different data abstraction
  • and different flow safe-approximation strategies,
    • i.e.,different transfer functions and control-flow handlings

Preliminaries of Data Flow Analysis

Input and Output States

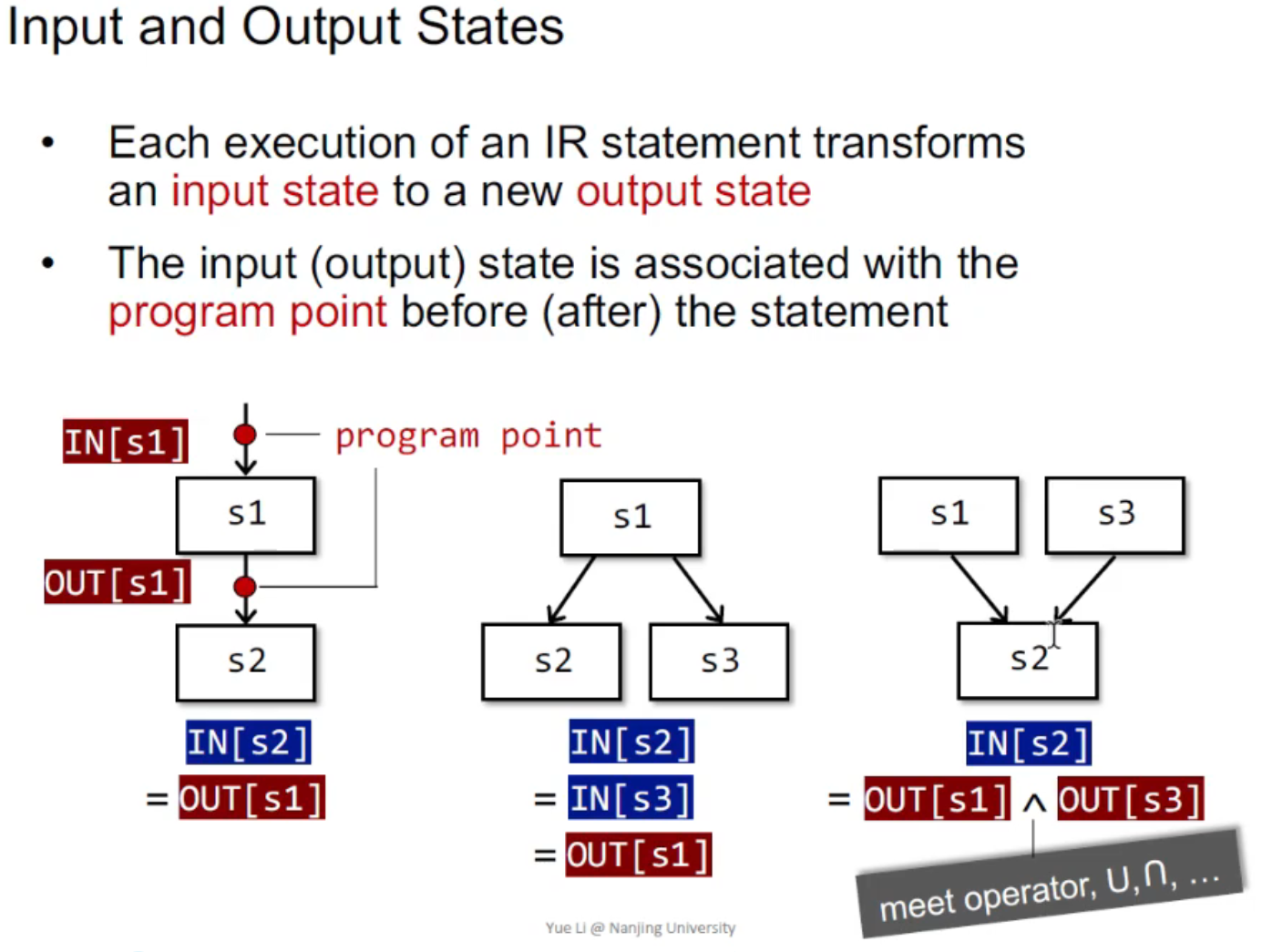
image-20240321115611349

总结：我们进行 data flow analysis 的目的是，对于每一个红点（program point），我们需要 associate it with a data-flow value that represents an abstraction of the set of all possible program states that can be observed at that point.

Notation for Control Flow Constraints

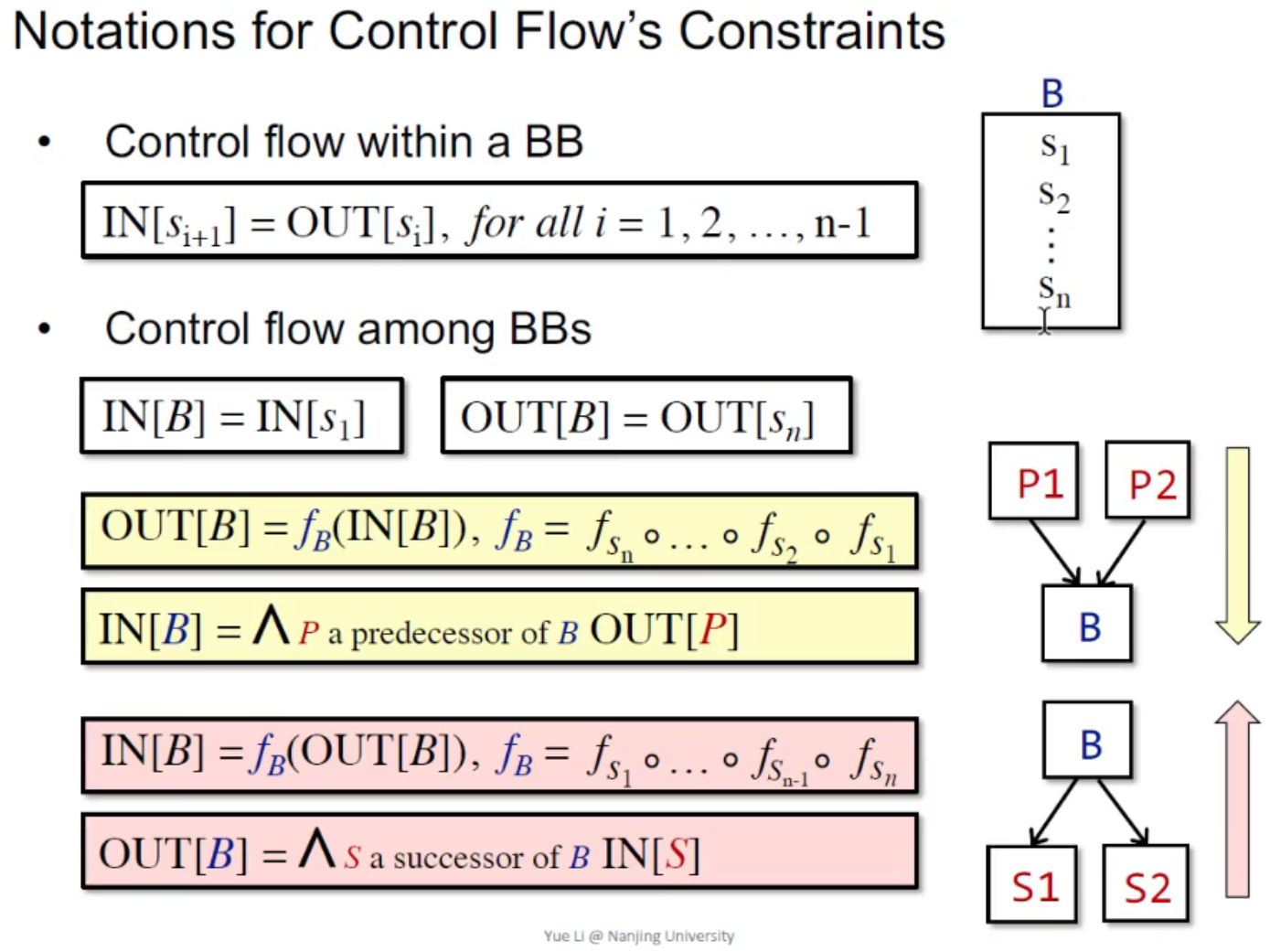
image-20240321120541423

如图，黄色的是 forward analysis，红色的是 backward analysis。

  1. Program point 是值
  2. statements 是转移函数
  3. basic block 是多个转移函数的复合（也是一个转移函数）
  4. basic blocks 之间传递信息的时候，需要用到 \(\bigwedge\) 符号进行聚合

总结：我们进行 data flow analysis 的方法是，find a solution to a set of safe-approximation-directed constraints on the IN[s]'s and OUT[s]'s,for all statements s.

  • constraints based on semantics of statements (transfer functions)
  • constraints based on the flows of control

Reaching Definitions Analysis

定义：A definition d at program point p reaches a point q if there is a path from p to q such that d is not "killed" along that path

也就是说：我在 p 处刚定义了 d，如果有一条路径能从 p 到 q，而且其中 d 没有被重新定义，那么，就说 d 可以 reach p。

  • 由于有路径 ≠ 程序实际上会走那条路径，reaching analysis 其实是 may analysis

例子 1

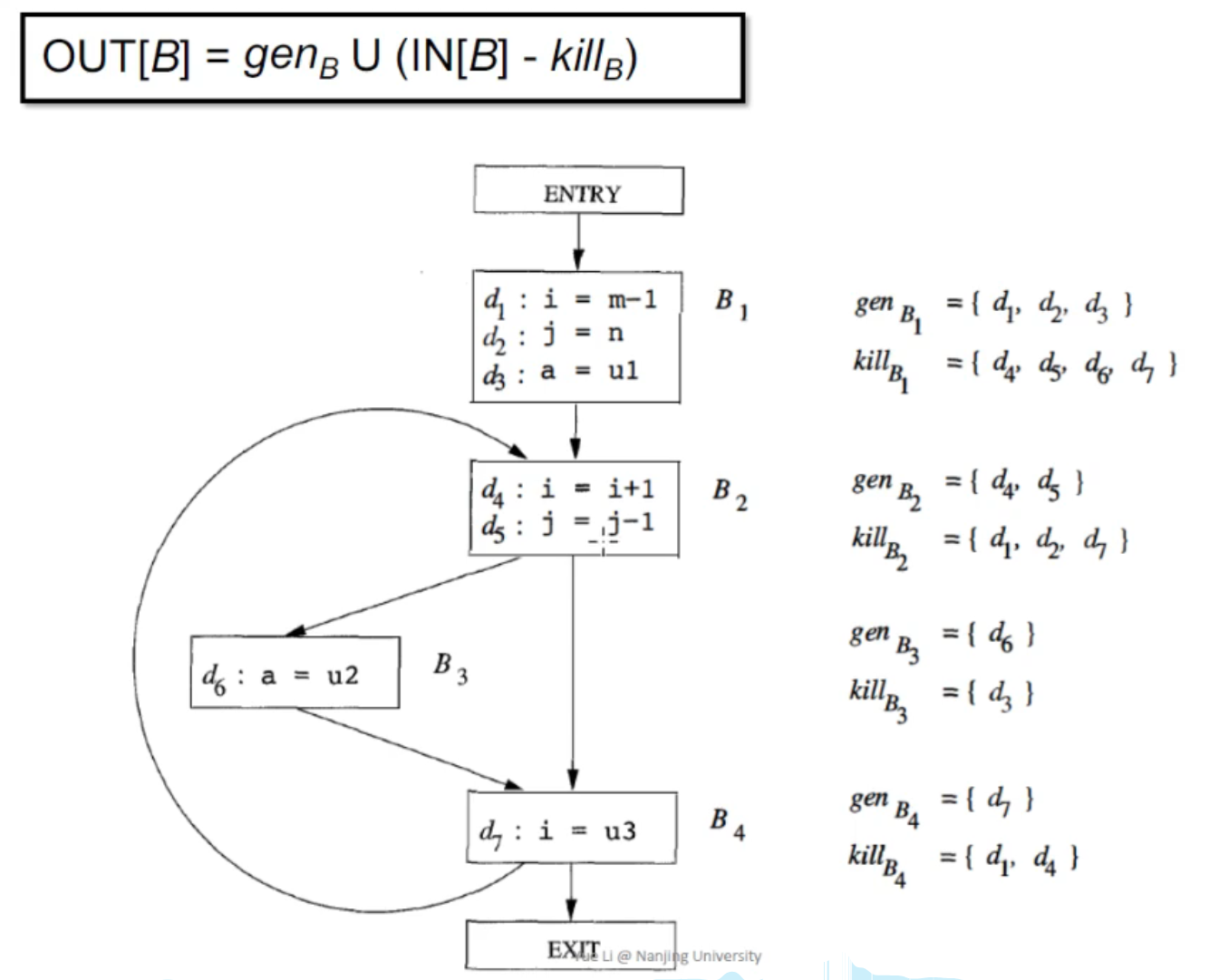
image-20240321124113746

如图，对于 B1，由于 d1: i, d2: j, d3: a，因此，

  • d1 -> i -> kills d4, d7
  • d2 -> j -> kills d5
  • d3 -> a -> kills d6

从而：\(kill_B = \set {d_4, d_5, d_6, d_7}\)

下面，我们给出一个完整的定义：

  • Transfer function：\(OUT[B] = gen_B \bigcup (IN[B] - kill_B)\)
  • Control flow: \(IN[B] = \bigcup_{P\text{ a predecessor of }B} OUT[P]\)
    • We use over-approximation as safety requirement here

从而，算法如下：

image-20240321132202774

例子 2

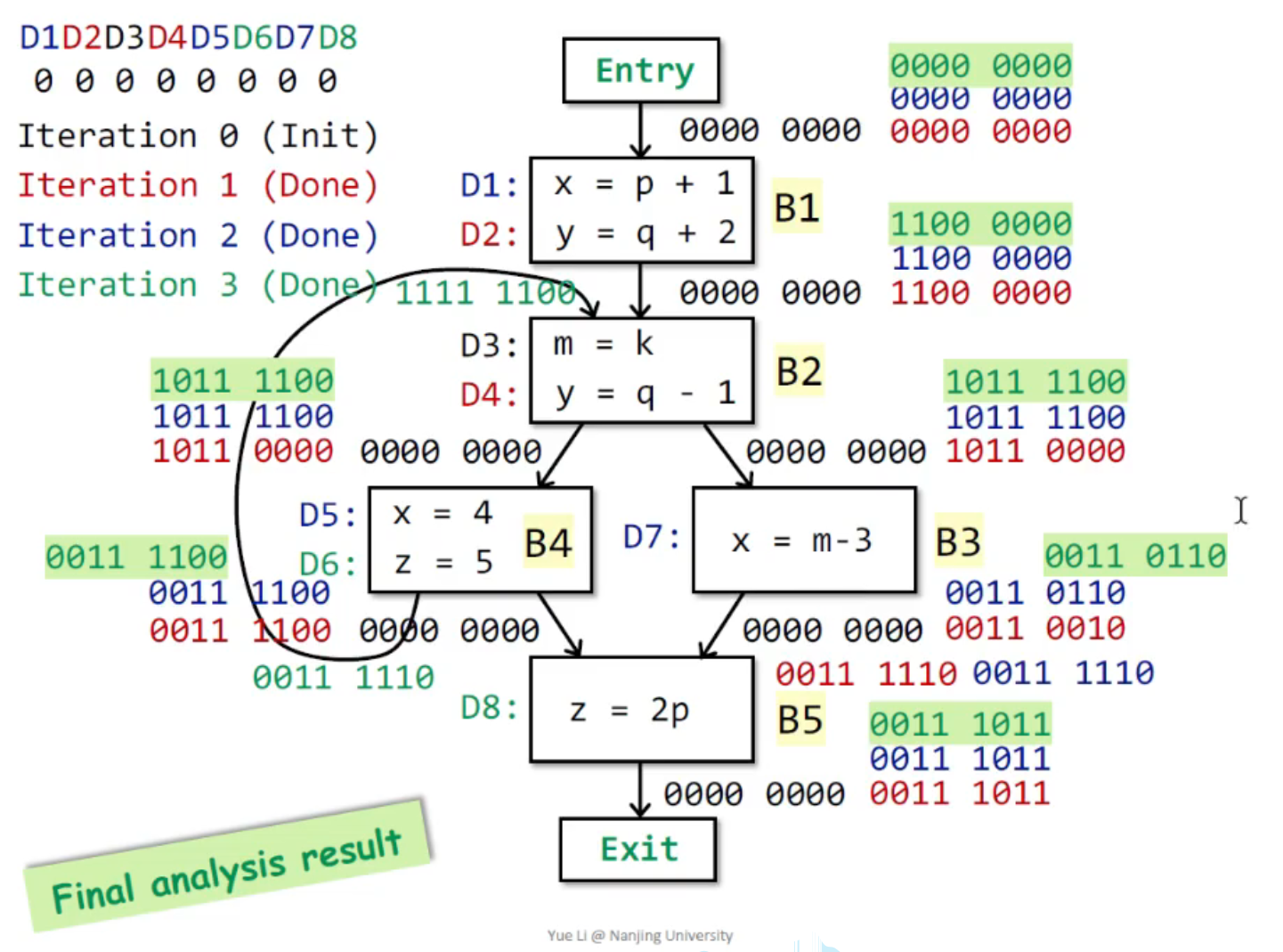
image-20240321131732668

Why this iterative algorithm can finally stop?

我们令 \(B_n(x)\) 为 \(B_n\) 在第 X 轮时的输出。

不难发现：\(B_n(x)\) 只和 \(B_{n}(x-1), B_{n+1}(x-1), \dots, B_{N}(x-1), B_1(x), B_2(x), \dots, B_{n-1}(x)\) 有关。

从而，严格地说，如果 \(\forall n \geq n_0: B_n(x-1) \subseteq B_n(x) \land \forall n < n_0: B_n(x) \subseteq B_n(x+1)\)，那么：\(B_{n_0}(x) \subseteq B_{n_0}(x+1)\)。

通过数学归纳法，我们不难证明：\(\forall n, x: B_{n}(x) \subseteq B_{n}(x+1)\)。

因此，如果有 changes to any OUTPUT occur，则必然递增前是递增后的严格子集，也就是 \(B_n\) 呈单调增加。

由于集合最大只能是所有 \(B_n\) 全满，因此，迭代的次数必然小于 \(N * \# \text{ of definitions}\)。从而，一定可以 stop。

Why we end when OUT stay that same?

如果 OUT stay the same，就会有 \(B_{n}(1, \dots, n) = B_{n-1}(1, \dots, n)\)。

从而，下一轮中，

  1. \(B_{n+1}(1) = f(B_n(1, \dots, n)) = f(B_{n-1}(1, \dots, n)) = B_{n}(1)\)
  2. 根据 (1)：\(B_{n+1}(2) = f(B_{n+1}(1), B_n(2, \dots, n)) = f(B_{n+1}(1),B_{n-1}(2, \dots, n)) = B_{n}(1)\)
  3. 根据 (1), (2)：\(B_{n+1}(3) = f(B_{n+1}(1,2), B_n(3, \dots, n)) = f(B_{n+1}(1,2),B_{n-1}(3, \dots, n)) = B_{n}(3)\)
  4. \(\dots\)

如此归纳，从而，\(n+1\) 轮中，所有的 \(B_{n+1}(x)\) 也都等于 \(B_n(x)\)。我们无需再迭代下去了。