Skip to content

4. Optimization

Lec 4: Optimization

Note: 下面的不同 formulae 之间，加减号、常数可能会不太一样。在实际中，不同人写的书、代码里面，也不尽相同。不过这些都无关紧要。

Stochastic Gradient Descent

Normal Gradient Descent:

\[ w_{t+1} = w_{t} - \alpha \nabla F(w_t) \]

where \(F(w) := \frac 1 N \sum_{i=1}^N L(x_i; y_i; w)\) is a multivariable function that take account for the whole dataset.

But actually, you can use a random minibatch of the whole set.

So, instead of \(F\), you can just use \(f\) here, where \(f := \frac 1 n \sum_{x \text{ from a random subset of size }n} L(x; y; w)\), and \(n \ll N\) or even \(n = 1\)

Problems

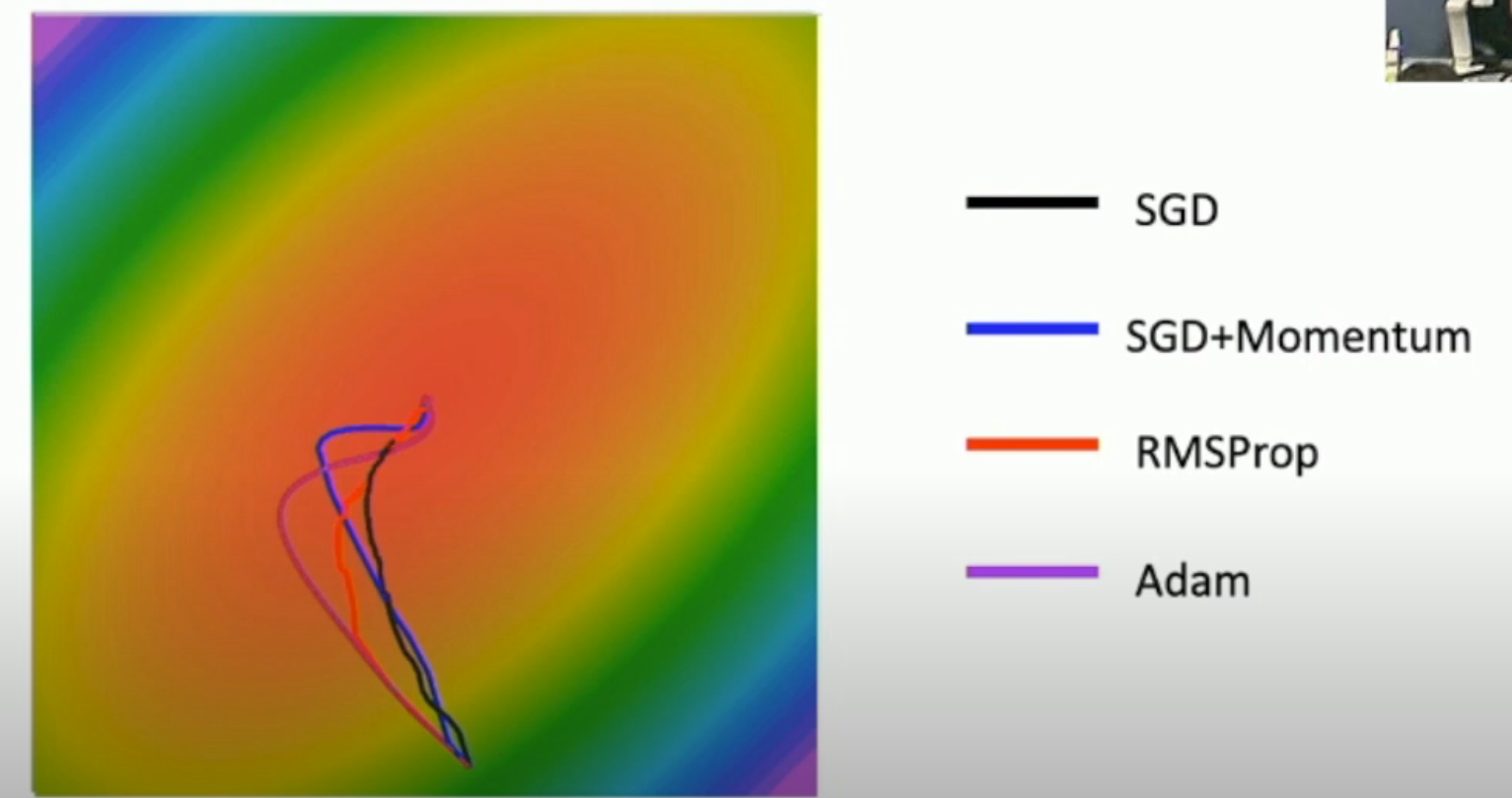
If the noise is big, the gradient might be really unstable, and make the descending route shape like this:

image-20240311004246773

That's partly because the loss function has a high condition number.

Momentum

\[ v_{t+1} = \rho v_{t} - \nabla \alpha f(w_t) \\ x_{t+1} = x_t + v_{t+1} \]

In the formula above, \(\rho\) is like the friction parameter (and the quicker, the more friction, the less \(\rho\)), and \(\nabla f(w_t)\) is like the force.

If you set \(\rho\) to zero, the formula degenerates to normal gradient descent.

Nesterov Momentum

\[ v_{t+1} = \rho v_{t} - \nabla \alpha f(w_t + \rho v_t) \\ x_{t+1} = x_t + v_{t+1} \]

We can simplify it by a change of variable \(\widetilde x_{t} := x_t + \rho v_t\), then:

\[ v_{t+1} = \rho v_{t} - \alpha \nabla f(\widetilde x_t) \newline \widetilde x_{t+1} = \widetilde x_t + \alpha v_{t+1} + \rho(v_{t+1} - v_{t}) \]

You can see the difference is that Nesterov momentum has \(v_{t+1} - v_t\).

AdaGrad & RMSDrop

\[ s_{t+1} := s_{t} + \nabla f^2(w_t) \newline x_{t+1} := x_t - \frac {\alpha\nabla f(w_t)} {\sqrt{s_{t+1}} + 10^{-7}} \]

但是，这样的话，\(s_t\) 只增不减，因此我们需要 decay rate \(\rho\)。这就是新方法 RMSDrop：

\[ s_{t+1} := \rho s_{t} + (1-\rho)\nabla f^2(w_t) \newline x_{t+1} := x_t - \frac {\alpha\nabla f(w_t)} {\sqrt{s_{t+1}} + 10^{-7}} \]

这样，\(s_t\) 就可以自适应地增减。

Adam

\[ \newcommand{\sone}{s^{(1)}} \newcommand{\stwo}{s^{(2)}} \newcommand{\rone}{\rho_1} \newcommand{\rtwo}{\rho_2} \]

我们可以融合

  • 动量
  • 自适应学习率

从而得到 Adam 最优化方法（\(\sone\) 就是动量，\(\stwo\) 就是自适应变量）：

\[ \begin{aligned} \sone_{t+1} &:= \rone \sone_{t} + (1-\rone) \nabla f(\sone_t) \newline \stwo_{t+1} &:= \rtwo \stwo_{t} + (1-\rtwo) \nabla f^2(\stwo_t) \newline x_{t+1} &:= x_t - \frac {\alpha \sone_{t+1}}{\sqrt{\stwo_{t+1}} + 10^{-7}} \end{aligned} \]

不过，这样还不够。因为初始的时候，如果 \(\rtwo\) 太小，那么 \(\sqrt{\stwo_{t+1}}\) 就可能会比 \(\sone_{t+1}\) 小得多。因此实际算法中，还会有一个 bias correction。

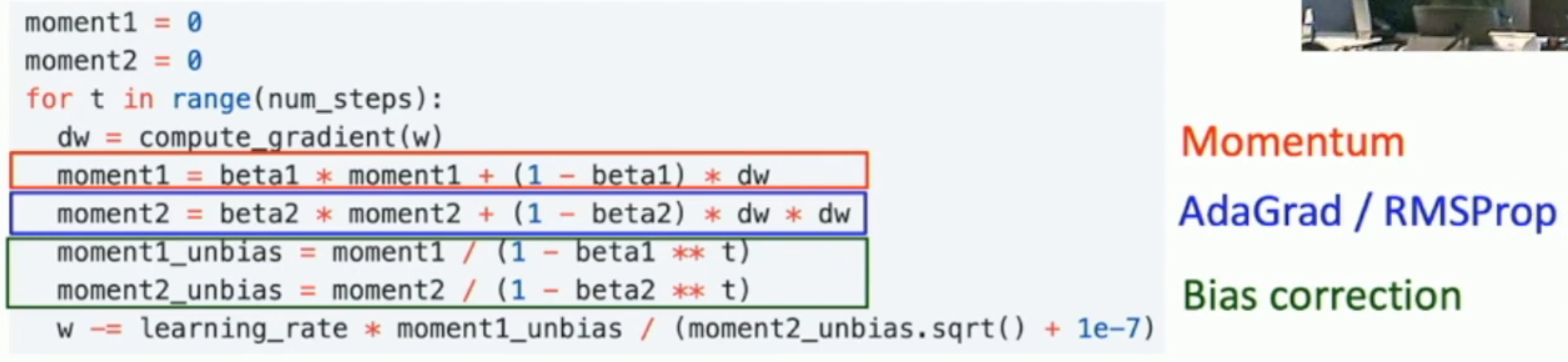
image-20240311014405721

Adam in Action

image-20240311014535475

因此，Adam 优化方法，直到现在，也没有过时。

Comparison Between These Optimizers

image-20240311015628976

一阶优化和二阶优化

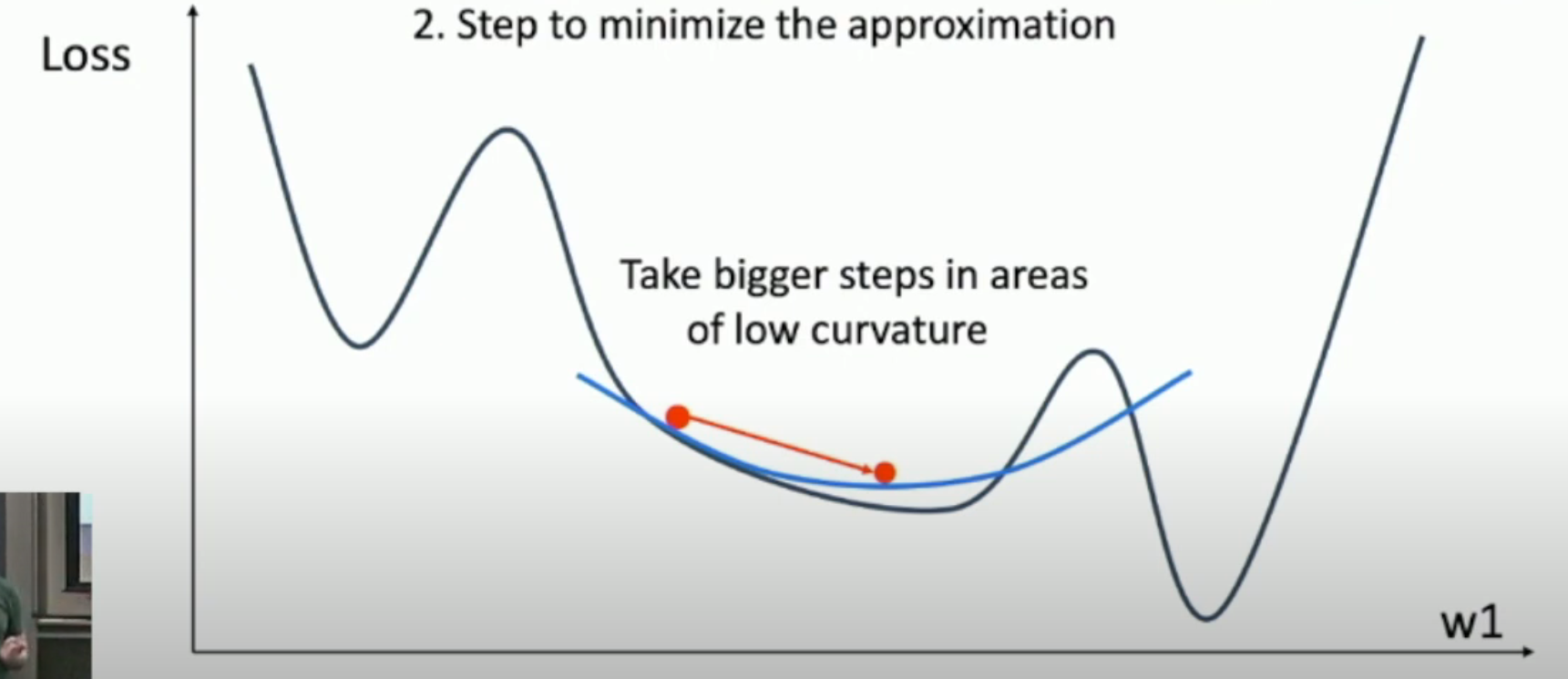
二阶优化的 robustness 往往强于一阶优化（如下图，我们如果知道了 Hessian matrix，就可以根据其得到曲率，从而适当加大 step）。

  • 不过，由于 SGD+Momentum 和 AdaGrad 对过往的梯度进行了累加，从而得到了和 Hessian matrix 类似的信息。

image-20240311022134280

当然，由于二阶优化涉及到了矩阵（而且还要通过矩阵的逆来求出二次曲面的极小值点，如下式），我们一般对于高维数据，不会使用二阶优化的方法。

\[ L(w) \approx L(w_0) + (w-w_0)^T \nabla_w L(w_0) + \frac 1 2 (w-w_0)^T \mathrm{H}_wL(w_0)(w-w_0) \]

从而，该二次曲面的最小值点就在：

\[ \nabla_w L(w_0) + (w - w_0)^T \mathrm{H}_wL(w_0)= w_0 - (L(w_0)\mathrm{H}_w)^{-1}\nabla_wL(w_0) \]
  • 注意算式中要对 Hessian 阵取逆。由于 Hessian 矩阵是稠密矩阵，因此没什么好方法，一般而言，复杂度就是在 \(\mathcal O(n^3)\) 这个量级的。

In Practice

  • Adam is a good default choice in many cases. SGD+Momentum can outperform Adam but may require more tuning
  • If you can afford to do full batch updates and the dimension is low, then try out L-BFGS (and don't forget to disable all sources of noise)