Skip to content

Problems With Deep Neural Network

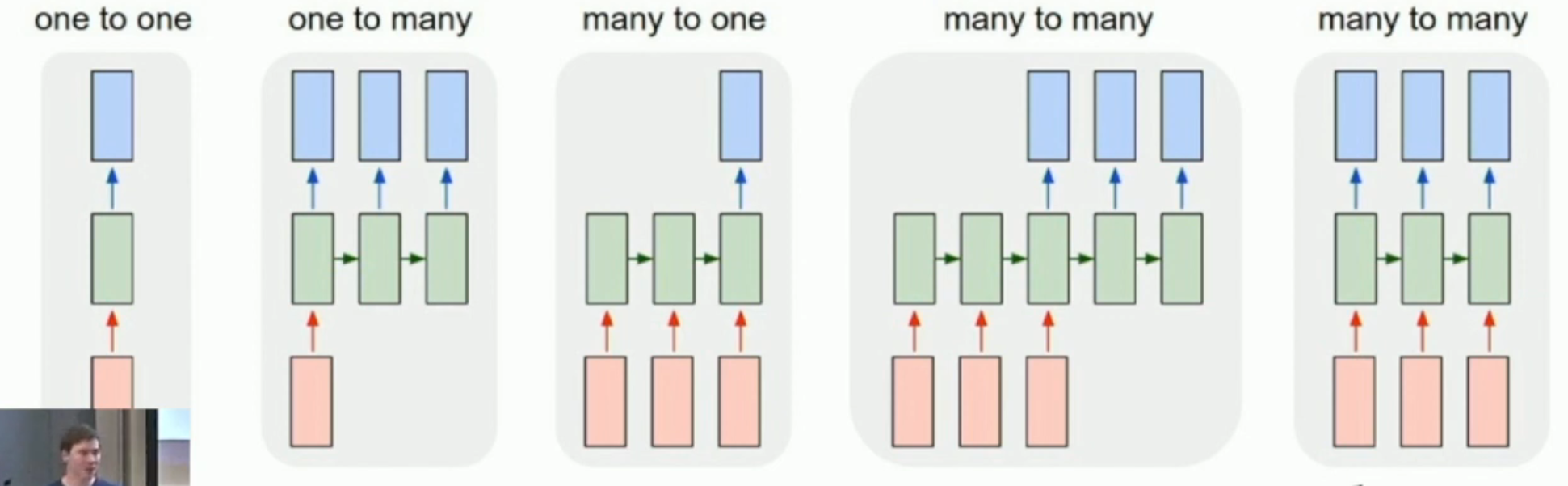
image-20240327014014615

Deep neural network，本质上还是一种前馈神经网络。因此，一般情况只能处理 one-to-one problems。

然而，如果输入/输出中，存在任意长的序列，而且这个序列的前后之间还是有关的（一般而言，临近的内容关系更大）。比如说：

  1. one-to-many problem：一张图片生成一段话（话可以任意长）
  2. many-to-one problem：一句话生成一张图（话可以任意长）
  3. many-to-many problem：语言翻译（翻译内容可以任意长）
  4. aligned many-to-many problem: 逐帧视频分类（比如说，确定 NSFW 的帧，视频可以任意长）

如果序列任意长，但是前后无关，那么我们就用前馈网络；如果序列固定长，前后相关，那么卷积神经网络之类的也许也能用。

但是如果序列任意长，而且前后有关，不仅如此，相关性还可能任意远（比如一本书的一个人名），那么，无记忆的前馈网络就不管用了。

  • In fact, we can also process non-sequential data in a sequential way. 比如图像分类等等。

Recurrent Neural Network

image-20240327015854923

RNN 和状态机类似，不过状态是连续的（理论上）。使用数学语言表达，就是： $$ h_t = f_W(h_{t-1}, x_t) $$ 而输出就是： $$ y_t = g_V(h_t) $$

RNN Computational Graph

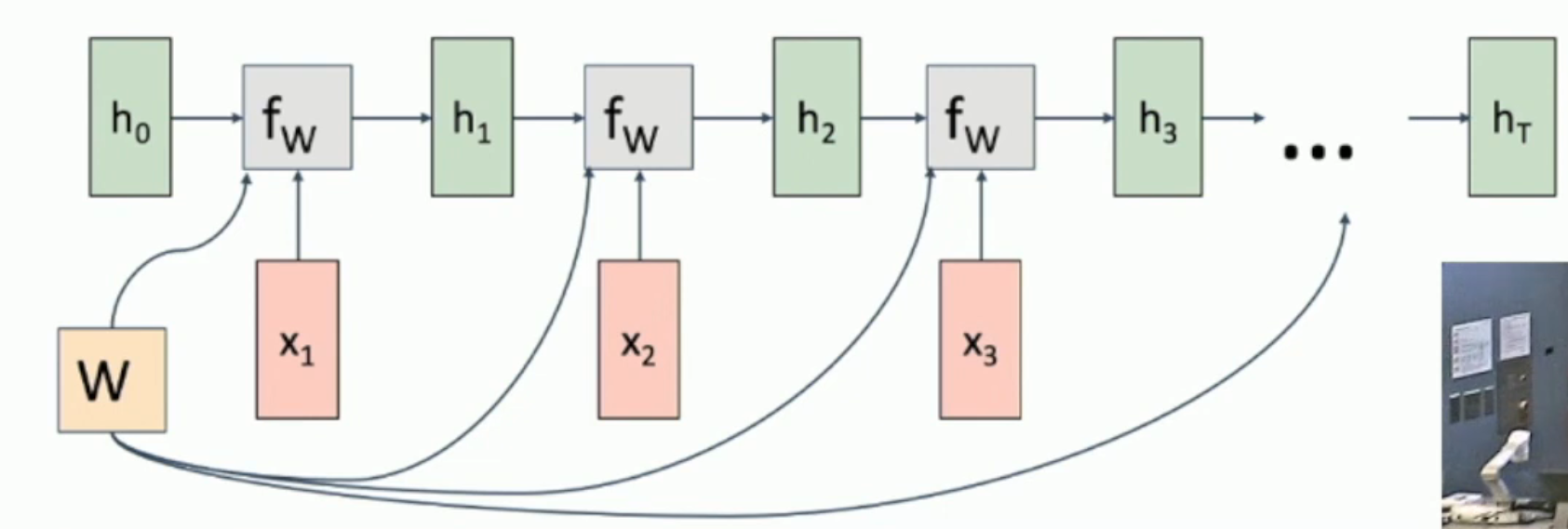
image-20240327025423104

如图，我们 reuse the same weight every time。因此，求导的梯度需要叠加。

Many To Many

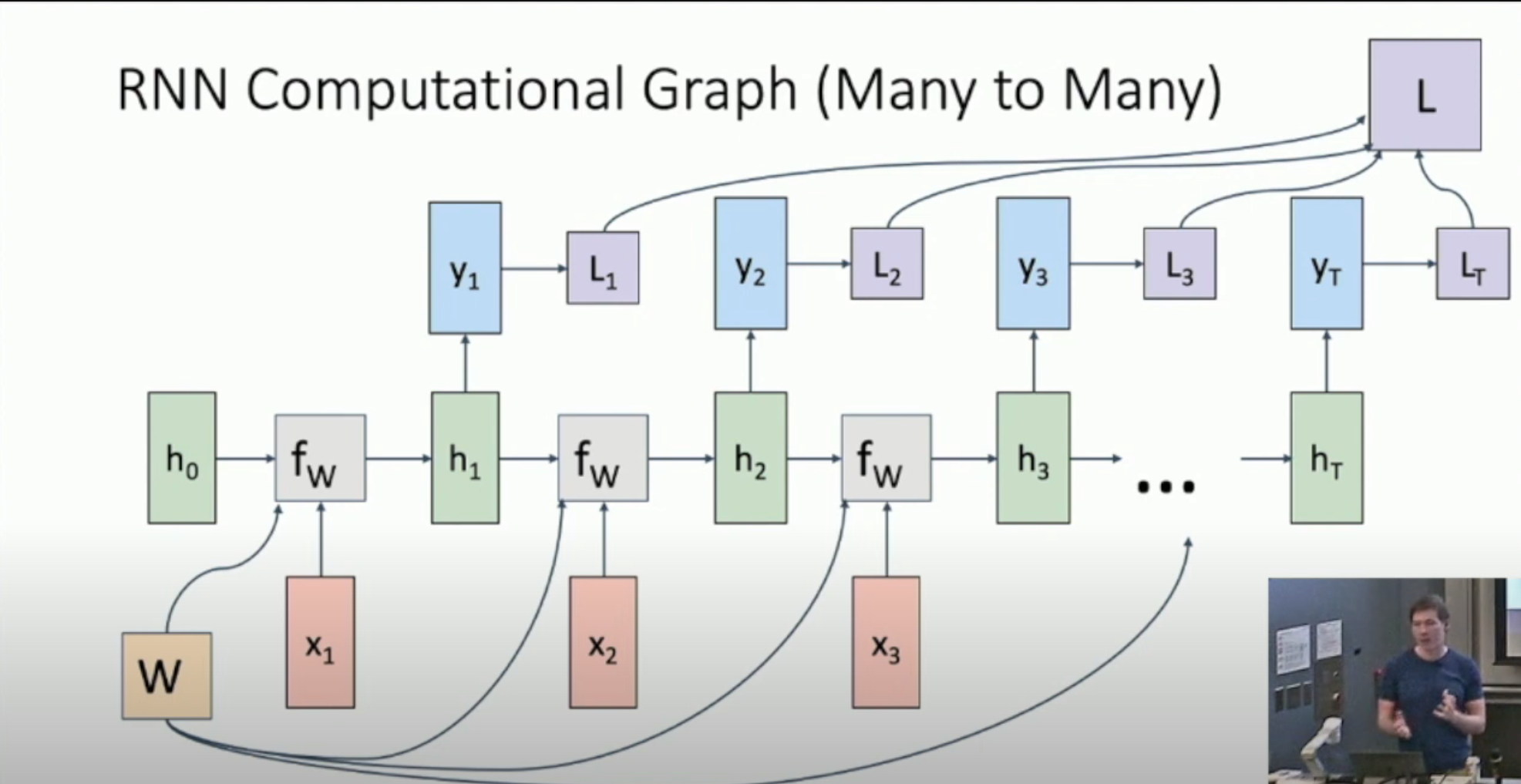
image-20240327044410561

如图，我们输出每一个 \(y_t\)，并得到 \(L_t\)，最终聚合成 \(L\)，并进行反向梯度传播。

Many To One

类似，只不过只有最后一个 \(h_T\) 输出成 \(y_T\)。

Sequence To Sequence

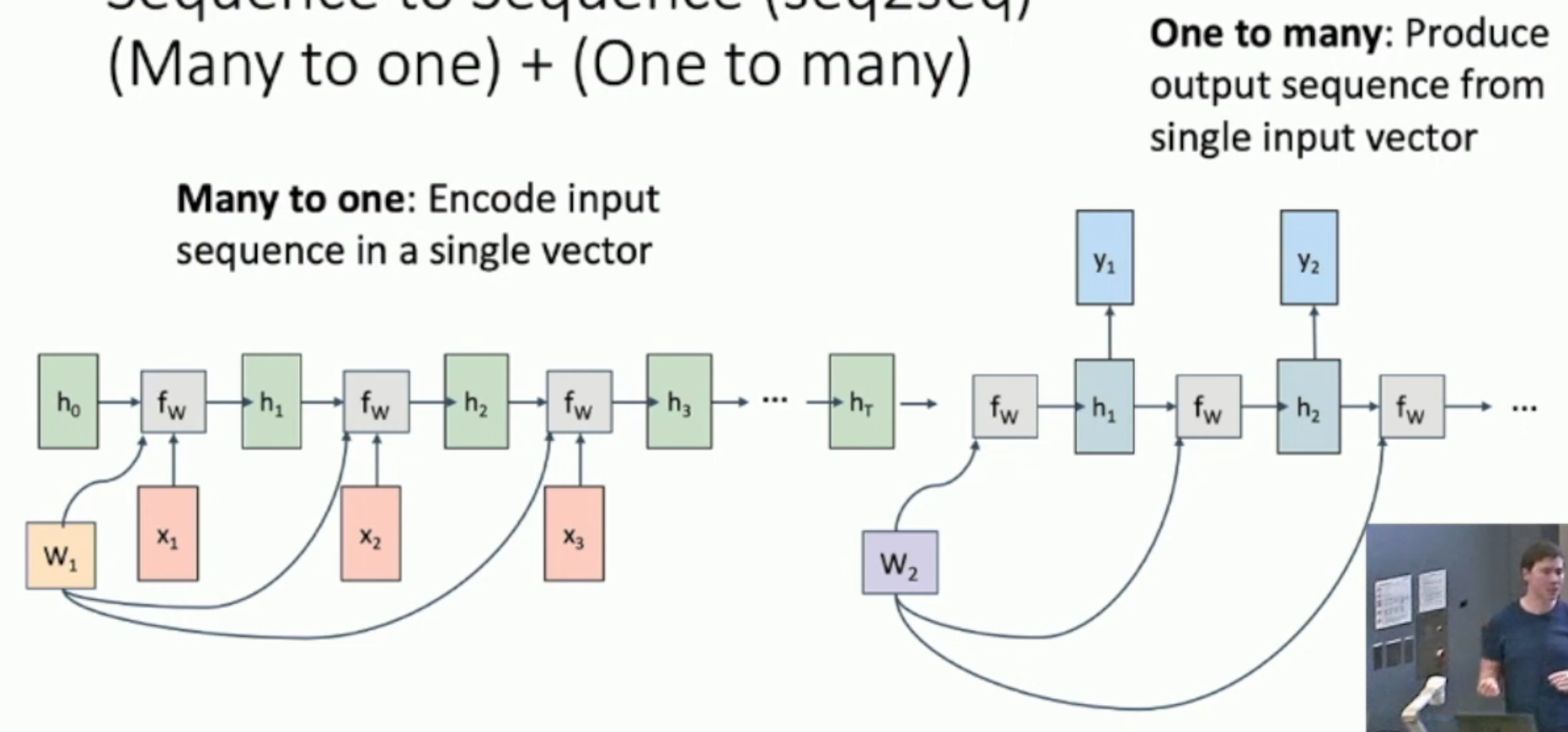
image-20240327044820033

如上图，如果我们希望生成和输入串的长度不一样的 sequence，那么就要用到 first many to one then one to many 的方法。

Example: Language Modeling

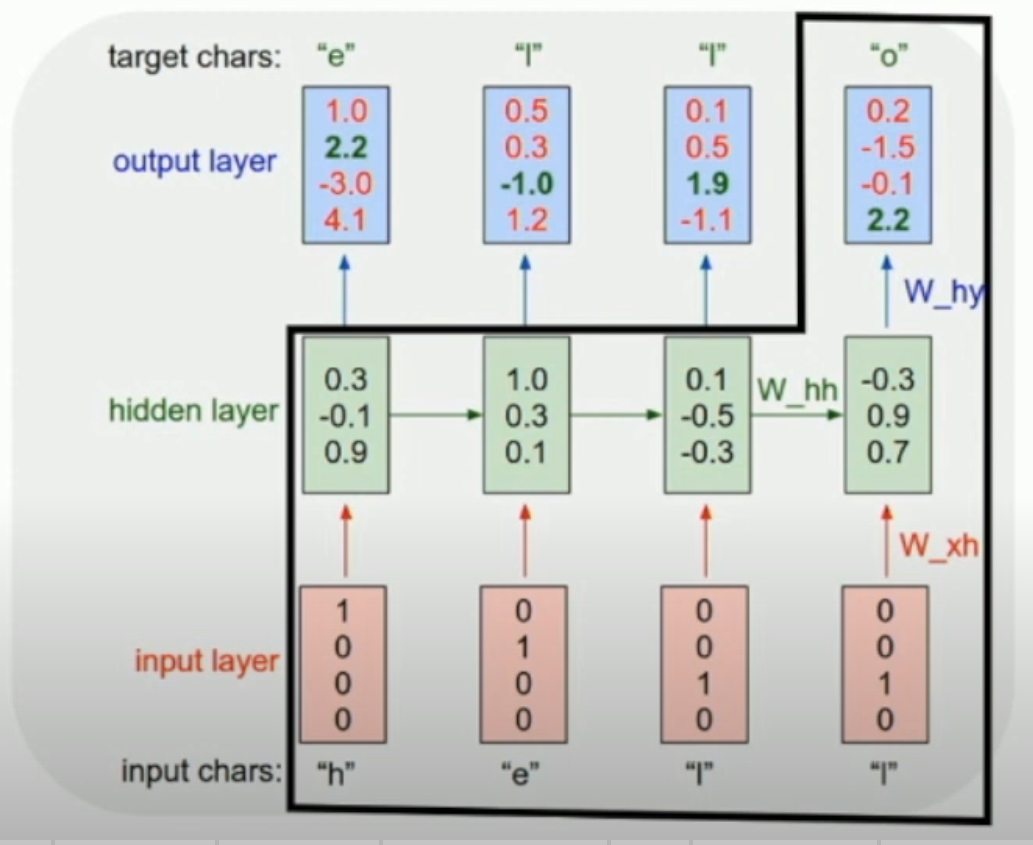
image-20240327050050195image-20240327050310944

如左图，我们可以通过图中这样的方式训练这个 RNN，使得：给定一段字母，我们就可以预测下一个字母。

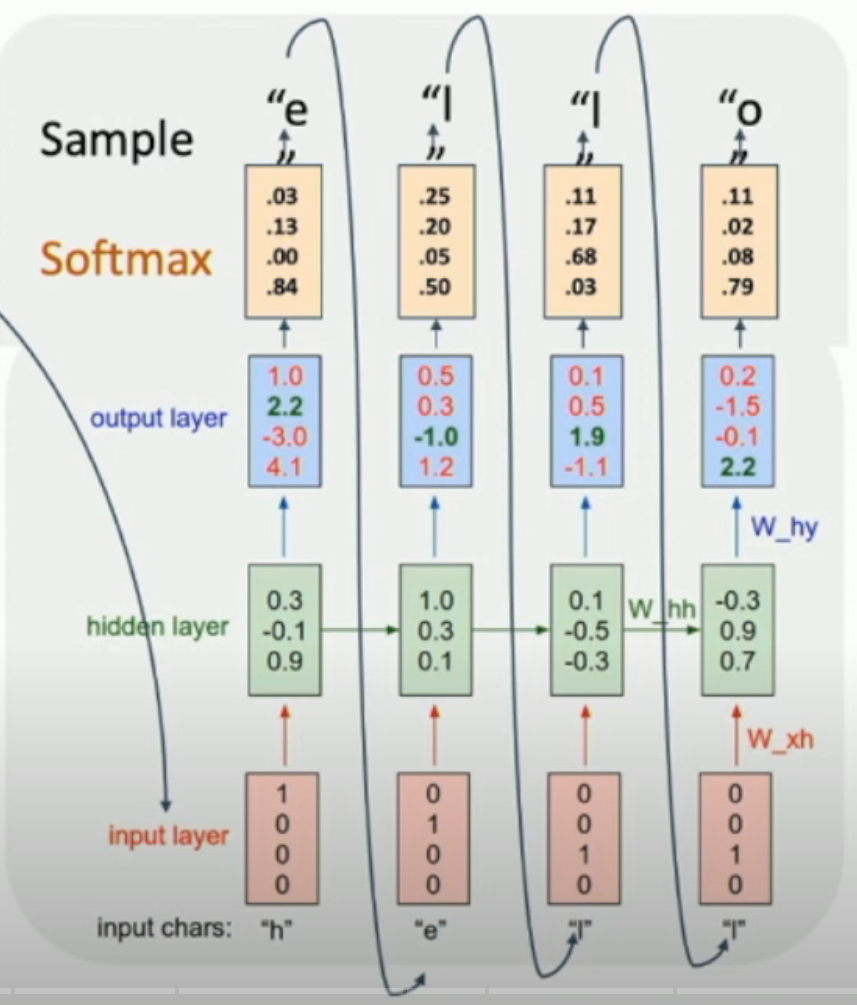
从而，在 testing 的时候，我们可以不断地把下一个字母当作下一个 input，然后不断地进行预测（如右图）。

  • 具体地，我们可以得到下一个字母的一个 distribution，然后从里面抽样作为实际的输出+下一个 input

另外，由于 input 是 one-hot encoding，乘法本质上相当于 column extraction。

因此，我们往往会通过 embedding layer，将稀疏的 one-hot encoding 变成 dense (, more expressive and maybe lower-dimensional) vector：

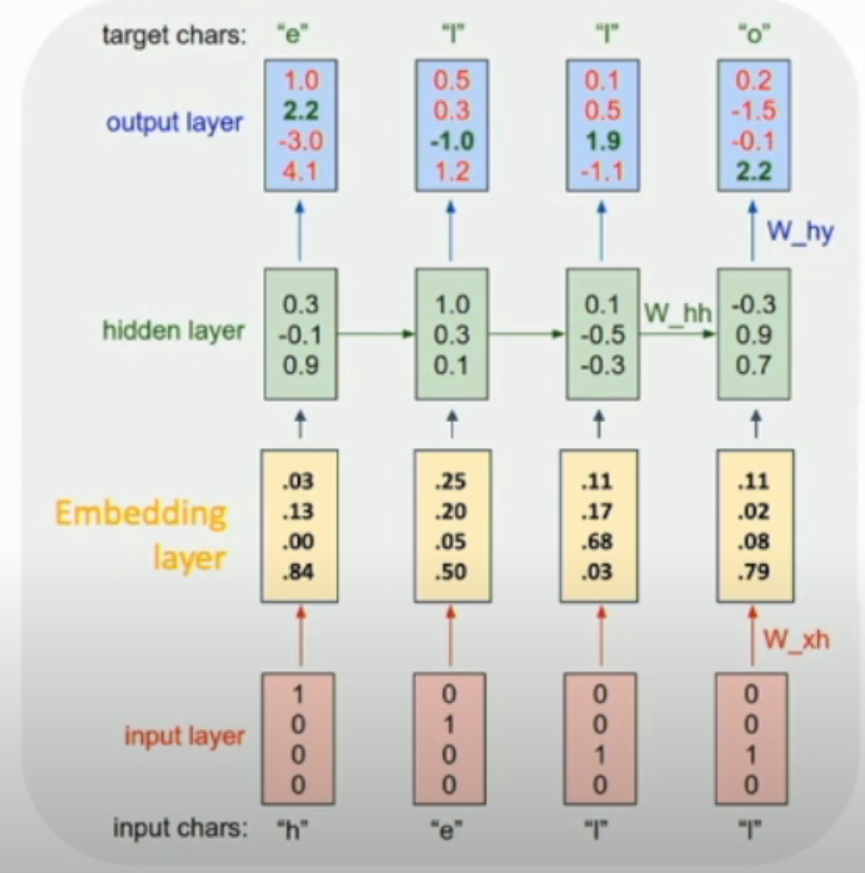
image-20240327050743369image-20240327050803162

Interpretability of Hidden State

对于 hidden vector 的一个 index：

  1. 我们可以通过让一个 recurrent neural network 通过上面的方式，不断预测出下一个字母，生成一段文本。
  2. 然后，对于文本的每个 letter，我们找到其 hidden state vector \(v_i\)，然后根据 \(v_i[index]\) 的大小，来对该文本进行染色。

对于一些 indices，我们有可能得到如下的文本：

image-20240328215406397

  • 说明至少人类不太能够解释。

在 Shakespeare dataset 中，对于另一些，我们可能可以得到：

image-20240328215605150

image-20240328215624048

  • 明显，分别是用来记录 quotes 和 line length 的。

在 Linux kernel code 中，我们可能可以得到：

image-20240328215753924

image-20240328215814958

image-20240328215824705

  • 明显，分别是用来记录 if-statements, quote and comments, and code depth 的。

Image Captioning

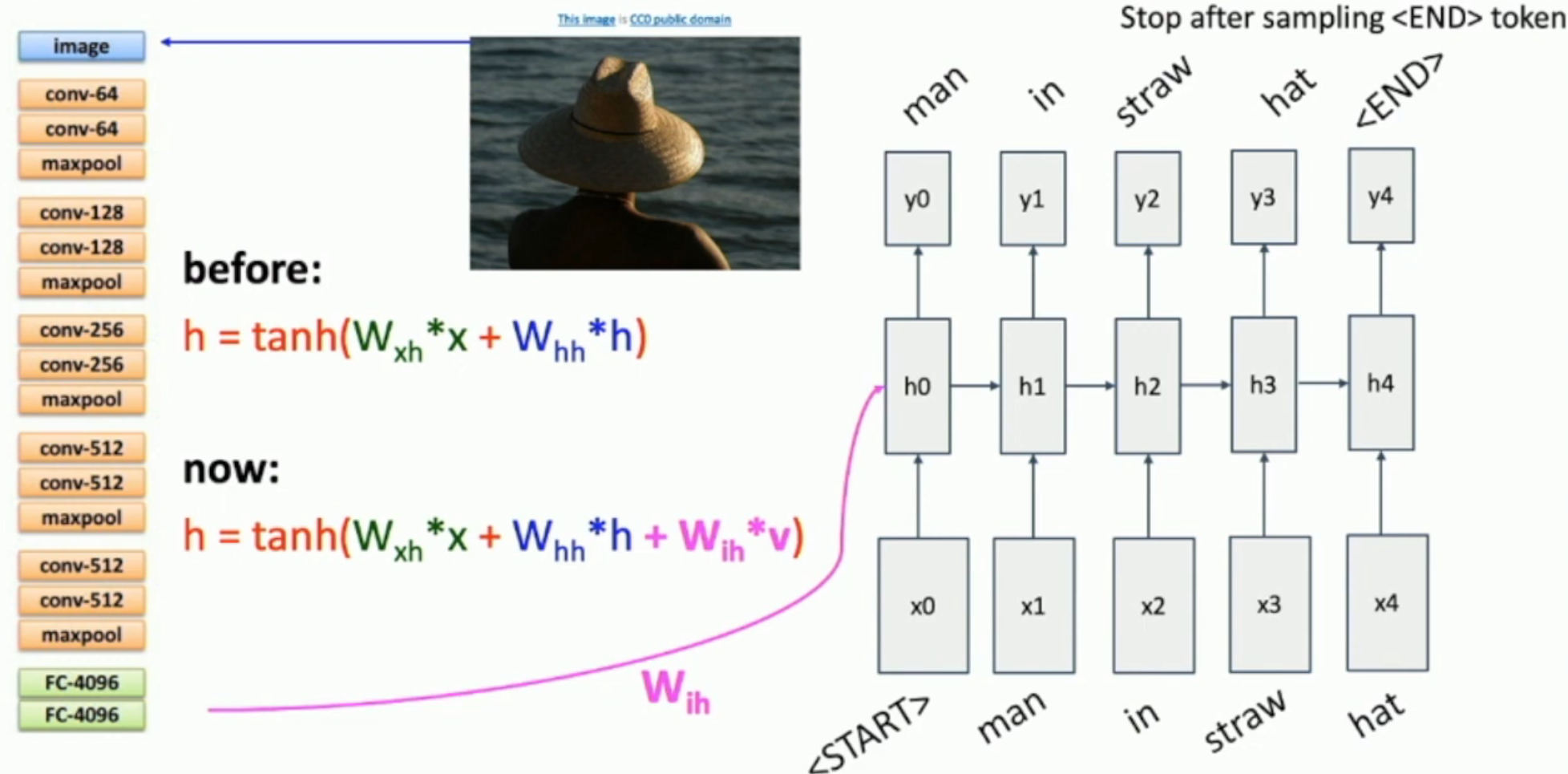
image-20240328222008312

如图，

  1. 我们将 pre-trained CNN 的全连接层去除，只保留最后的 feature vector（如图左所示）
  2. 我们稍微魔改一下 state transfer function（如图中所示），其中 \(W_{ih}\) 也是我们要训练的，而 \(v\) 是对应图片的 feature vector
    • 对于同样的图片，它会对应同样地 feature vector。因此，我们会在每一步都输入一样的 feature vector
  3. 多了两个单词：<START> 和 <END>。
    • 因为这不是任意长度的文本补全，而是 image2text
      • 没有初始文本
      • 需要程序自己停止继续生成

因此，我们其实就是通过增加一个 \(W_{ih}v\) 的方式，将图片的 feature 引入了文本生成之中。

Failure Modes

image-20240328224533566

Vanilla RNN Gradient Flow

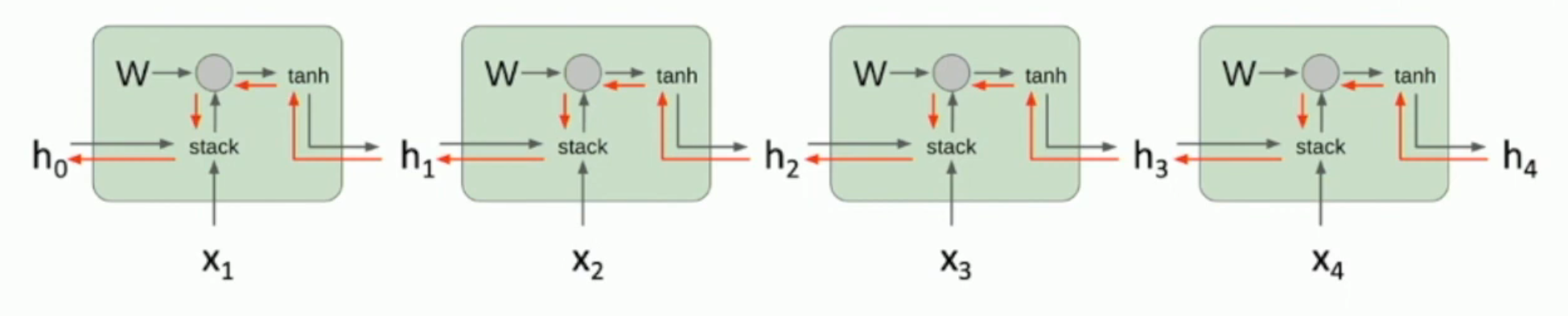
image-20240328231018945

如图，RNN 的梯度传播方式如上：每一次从 \(\frac {\partial loss} {\partial h_i}\) 传播到 \(\frac {\partial loss} {\partial h_{i-1}}\)，我们都需要乘以一个 \(W^T\)。从而（注意矩阵的 2-范数就是矩阵最大的奇异值）：

  • 如果 \(\|W^T\|_2 < 1\)，那么很可能会有梯度消失
  • 如果 \(\| W^T \|_2 > 1\)，那么很可能会有梯度爆炸

对于梯度爆炸，我们通过 gradient 的 2-范数，做一个 gradient clipping:

grad_norm = np.sum(grad * grad) # In fact, this is gradient norm squared
if grad_norm > threshold:
    grad *= (threshold / grad_norm)

对于梯度消失，我们也不敢放大梯度啥的，所以，我们就直接换模型——LSTM。

Long Short Term Memory Architecture

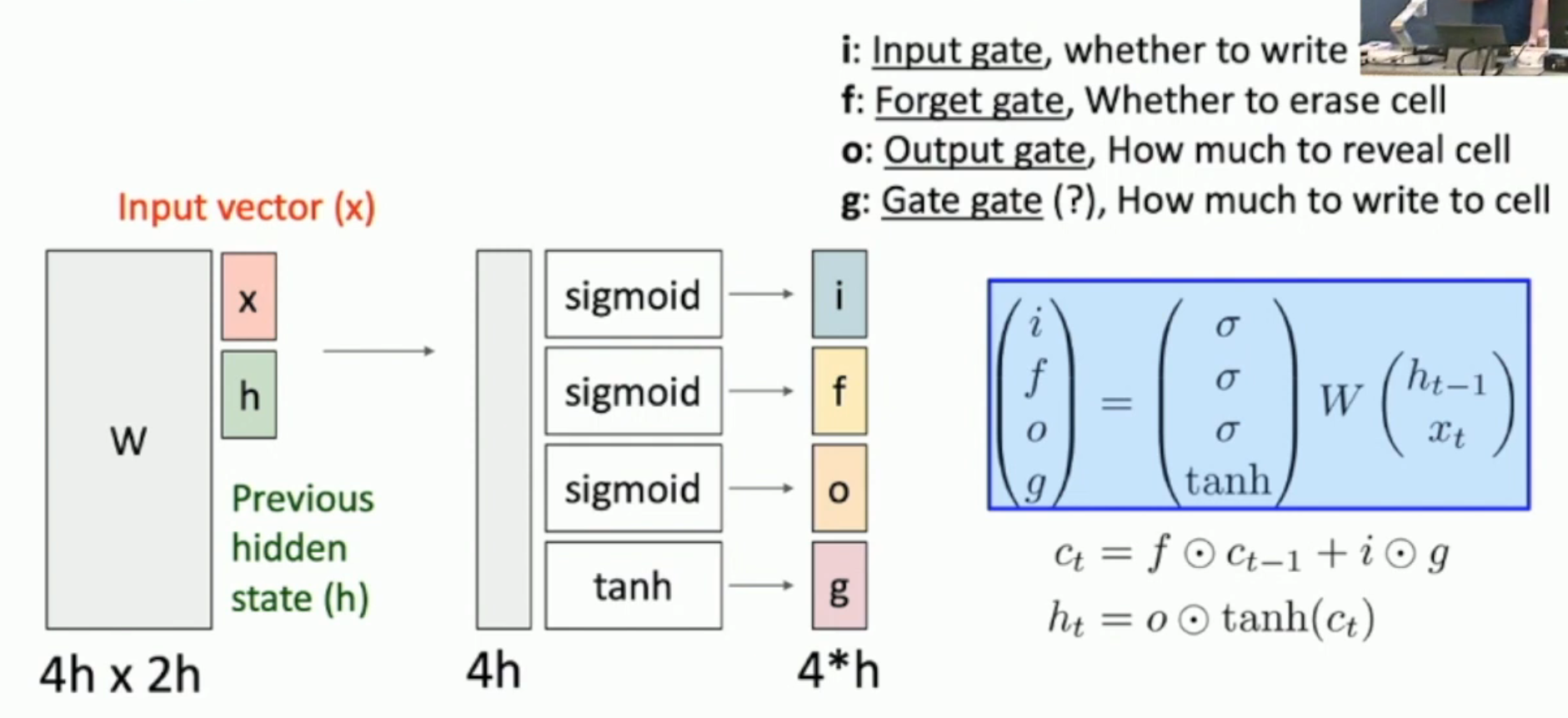
image-20240329055003539

直观上，LSTM 就是如图的矩阵乘法+state transfer。

  1. 上一个 state 和本轮输入，通过矩阵 \(W\)，产生出一个向量
  2. 将向量分为四块，然后通过 sigmoid 或者 tanh，形成
    1. input: 要把什么“内容”写入 cell？
    2. gate: 写多少“内容”？
    3. forget: cell 要忘记多少？
    4. gate: 最后，cell 需要表现出来多少？（表现出来的将被写入 hidden state）

How to solve gradient disappear problem?

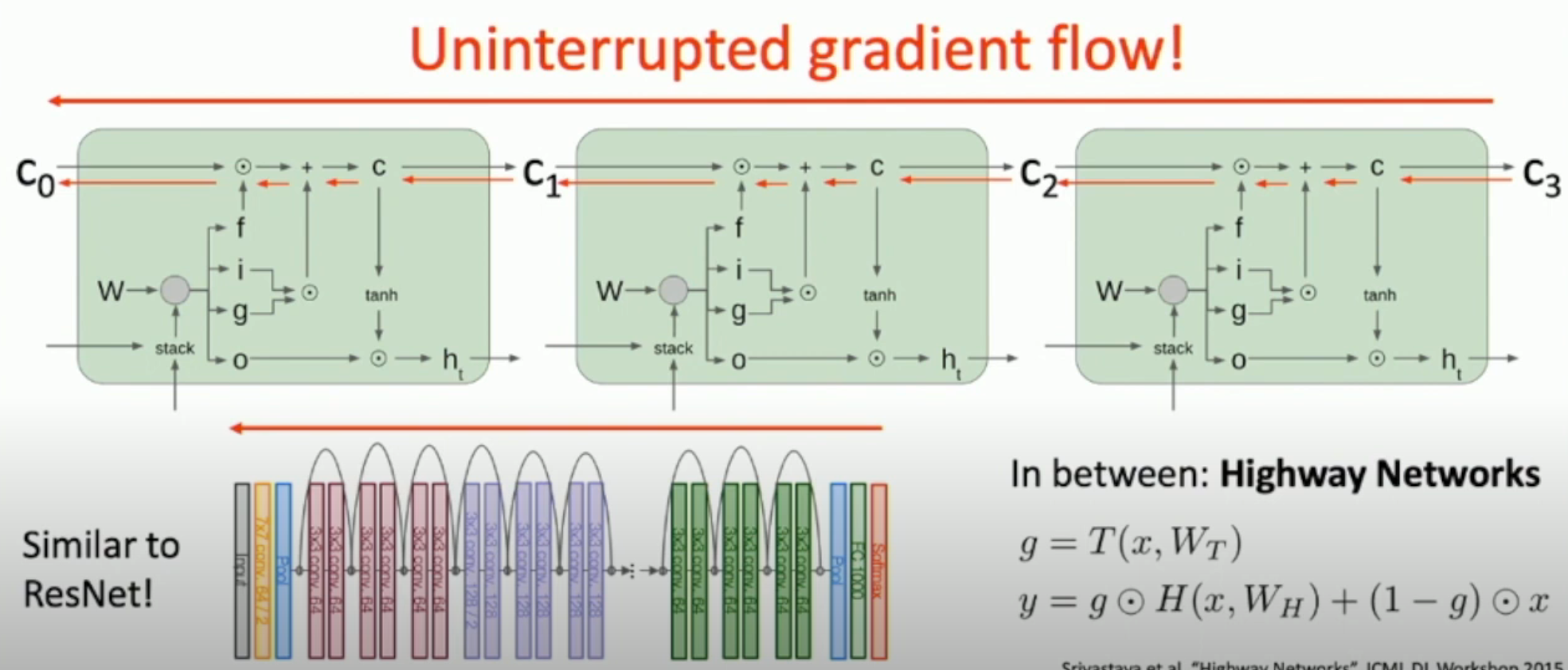
image-20240329054602813

如图，LSTM 的 cell state 有一条“高速公路”，“公路”上只有矩阵的 element-wise multiplication，其它都没有。

因此，可以保证在 \(f\) 不太小的情况下，梯度可以正常地传播回去。

  • 而如果 \(f\) 太小，则说明本身这就是一个用来遗忘的，本就应该之后和之前的值无关，i.e. 梯度本就应该不传回去

因此，如果梯度理应被传回去，那么，它就应该被传回去。

Multilayer RNN

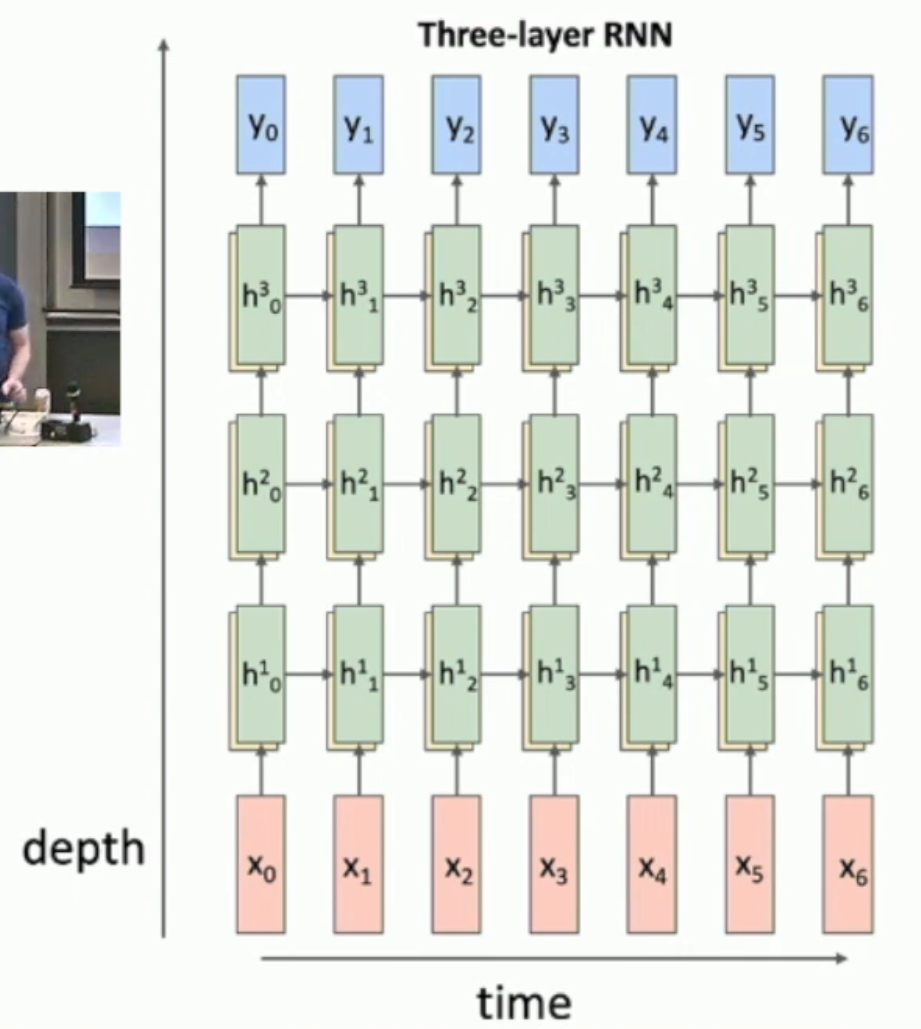
image-20240329055740551

如图，越多层的 RNN，就有越强的表现力。

Rules of thumb for RNN:

  1. LSTM tend to work well in most cases
  2. RNN structures with 3~5 layers are most common