Skip to content

Activation Functions

Sigmoid and Tanh

Problems:

  1. (Sigmoid) Not zero-centered
  2. (Sigmoid and Tanh) "Saturated" neurons "kill" the gradients [most concerning problem]
  3. (Sigmoid and Tanh) exp operation is a bit expensive
    • But this difference is mainly for CPU devices. For GPU, fetching data is the most expensive operation.

Problem 1

对于一个神经元而言： $$ output = f(\sum_i w_ix_i + b) $$ 如果它的输入也是 sigmoid，那么，所有 \(x_i\) 都是正数。

从而：\(\frac {\partial loss}{\partial w_i} = \frac {\partial loss}{\partial sum} \frac {\partial sum}{\partial w_i} = x_i \frac {\partial loss}{\partial sum}\)。因此，由于 \(\frac{\partial loss}{\partial sum}\) 固定，所有的 \(\frac{\partial loss}{\partial w_i}\) 要么全正、要么全负。

从而，我们只会向两个象限进行梯度下降（如下图），使得我们的梯度下降会蜿蜒曲折。

  • 在高维的时候，情况会指数级恶化

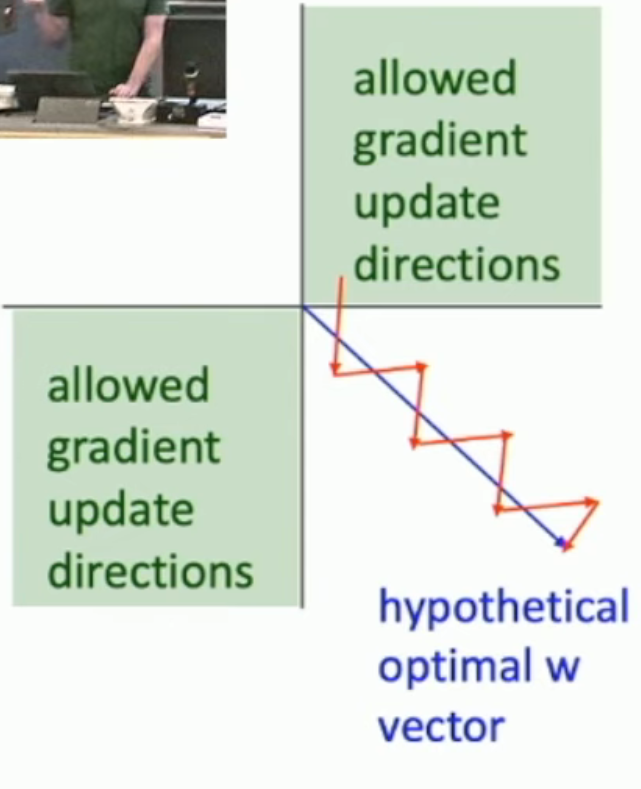
image-20240322211613722

不过，由于我们一般采用 minibatch 来训练。不同的 samples 的梯度会互相抵消。

ReLU Family

Merits:

  1. Do not saturate (in positive region)
  2. Very computationally cheap

Drawbacks:

  1. Still not zero-centered: but can be solved by minibatch
  2. If it's the case that if you use any data in the dataset as input, one of the layers gets all zero outputs (b/c of the weights and biases), then all the layers before this "all-zero" layer will be dead forever. Because "all-zero" layer cannot pass gradients.

解决方案

让负数区域不那么平坦：

image-20240322213748687

However, in practice, all ReLUs (including ReLU itself and its variations) are just fine.

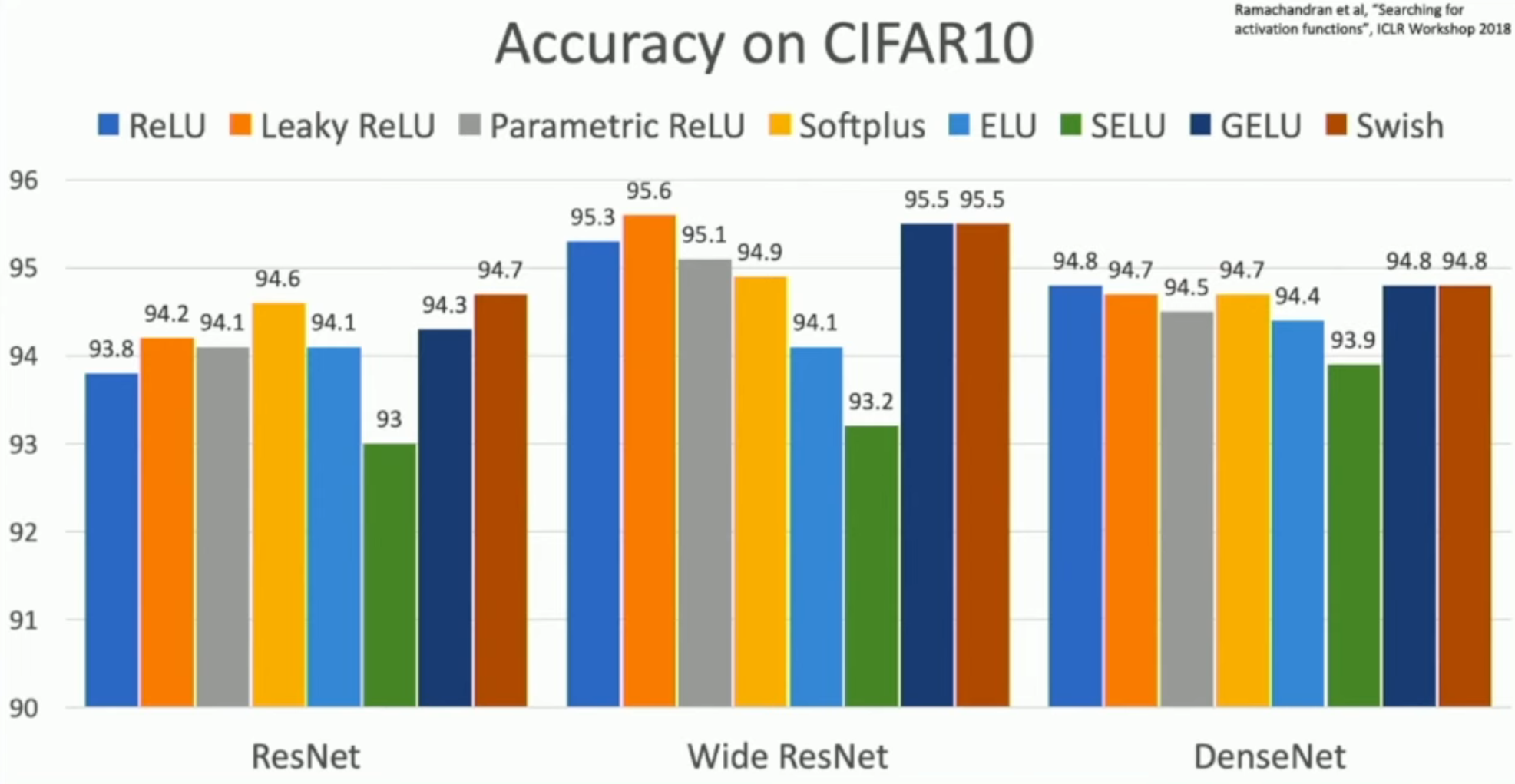
image-20240322215631680

Rules of thumb:

  • Don't think too hard. Just use ReLU
  • Try out Leaky ReLU ELU /SELU /GELUif you need to squeeze that last 0.1%
  • Don't use sigmoid or tanh

Data Preprocessing

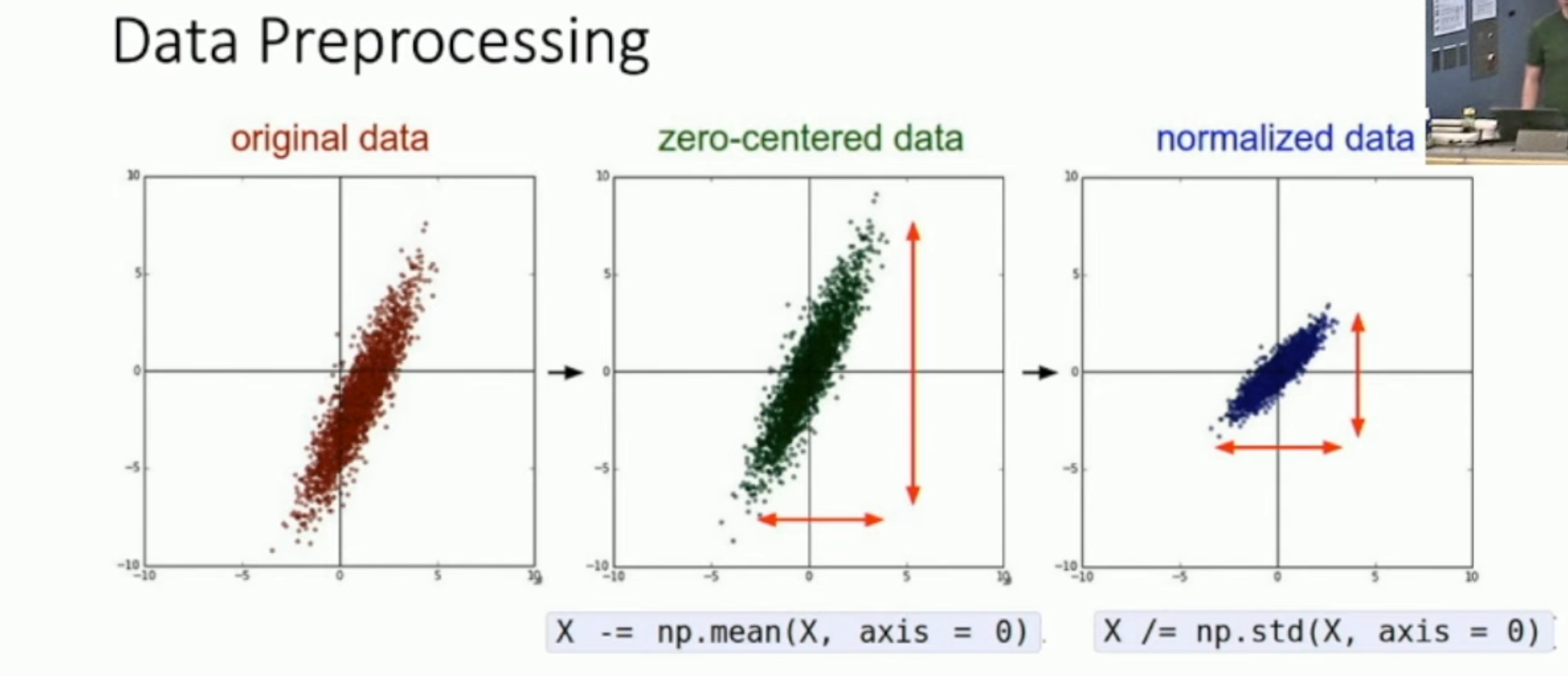
image-20240322221710863

如图，这就是最基础的 data processing。计算出一个 training set 的 mean 和 standard deviation（沿着每一个轴），然后将所有数据按照这样的变换（i.e. 减去 mean，再除以 standard deviation）来标准化。

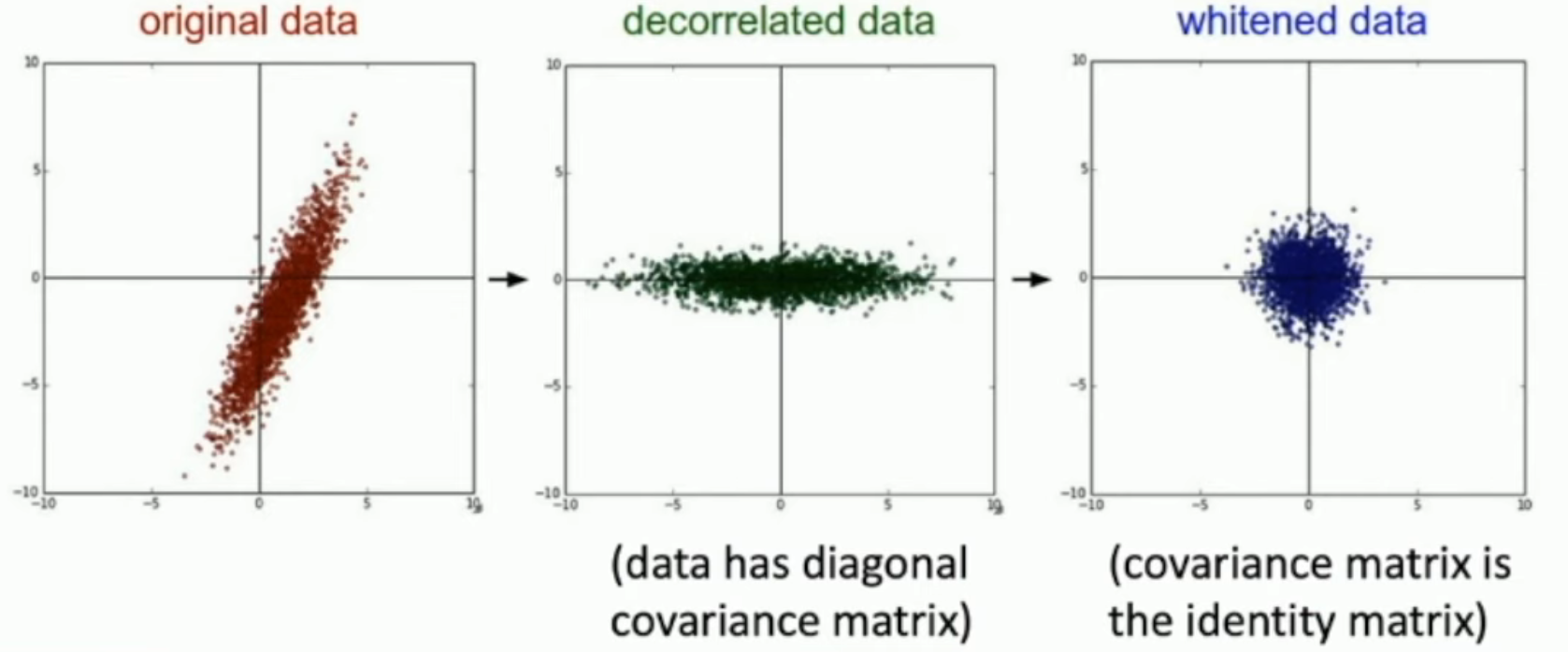
image-20240322221932135

实际上，我们可以在 zero-centering 和 normalization 之间插一步：通过奇异值分解的方法，找到一组标准正交基，使得两两之间的协方差都等于 0。

具体来说，对于 zero-centered data，如果我们希望求 \(\vec a, \vec b\) 两轴的均方差，那么： $$ E(ab) - E(a) E(b) = E(ab) \propto \vec \sum_{i=1}^N (W_i\vec a ) ( W_i\vec b) = \vec a^t W^t W \vec b = \vec a^t V \Sigma V^t \vec b $$ 如上，如果我们让所有的标正基在经过 \(V^t\) 变换之后，就是一组自然基，就可以。

因此，我们只需要求逆矩阵 \({(V^t)}^{-1} = V\)，让 \(V\) 构成这组标准正交基即可。

  • 注意：这里的所谓方差、期望值，都是通过已有的数据，通过最大似然推断的。

Why zero-centering?

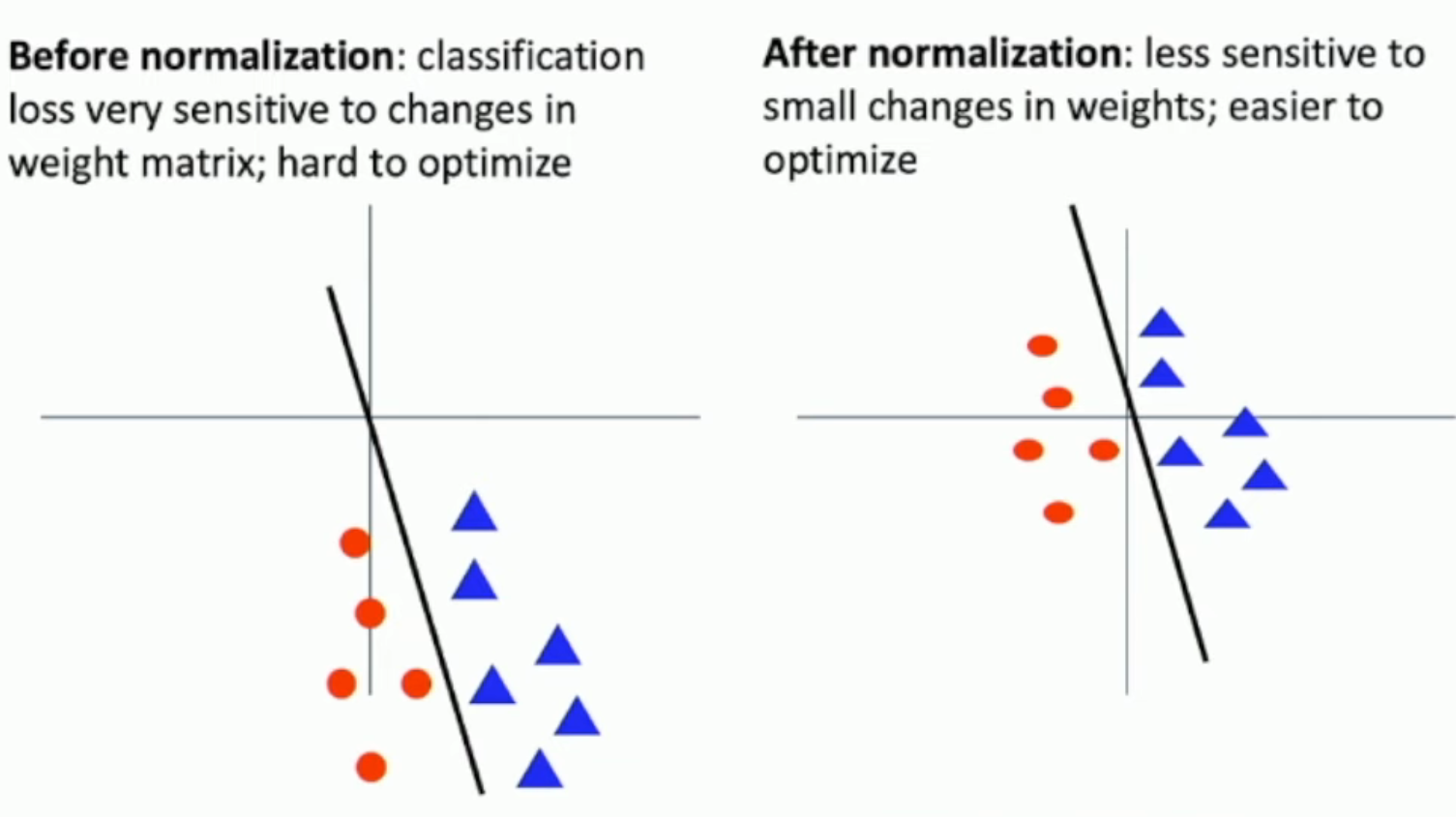
image-20240322231054995

如果没有 zero-centering，那么权重上很小的偏差，就会导致分类中很大的偏差（如左图，黑色稍微转一个角度，就会在红色和蓝色之间移动很大的举例）。

Data Processing for Images

image-20240322231414484

图片处理中，我们一般使用如上的 normalization 方法，而不使用 SVD。

Preprocessing the Testing Set?

在使用中，我们会对 test sample 进行和 training sample 一样的变换。

Relationship with Batch Normalization?

一般情况下，人们会先进行显式的 preprocessing，然后同时做 batch normalization。

Weight Initialization

Problem

image-20240322233222499

如图，假设每层的权重的标准差都一样，如果权重的标准差小了，就会导致后面的层的输出越来集中（如上图）。

从而，由于输出几乎为 0，因此下一层权重的 gradient 也会几乎为 0（remember: local gradient of weight equals to the output of the previous layer)

image-20240322233425495

假设我们使用的是 tanh 函数，如果大了，就会导致输出非常靠近 ±1。那么虽然 output 不小，但是过于接近 1，也会使得梯度太小。

Xavier Initialization

Xavier 初始化适用于 zero-centered non-linear function。

Key idea: initial weight of the current layer shouldn't change the standard deviation of the data of the previous layer.

也就是说：给定一个数据 \(\vec x\)，对于任何输出 \(\vec y\)，有：

\[ y_j = \sum_{i=1}^{Din} x_i w_{ij} \]

从而：

\[ \newcommand{Var}{\operatorname*{Var}} \newcommand{E}{\operatorname*{E}} \begin{aligned} \Var(y_j) &= Din * \Var(x_iw_i) \quad \text{[Assuming x, w are iid, respectively]} \\ &= Din * (\E(x_i^2) \E(w_i^2) - \E(x_i)^2 \E(w_i)^2) \quad \text{[Assuming x, w are independent]} \\ &= Din * \E(x_i^2)\E(w_i^2) \quad \text{[Assuming x, w are zero-centered]} \\ &= Din * \Var(x_i) \Var(w_i) \end{aligned} \]
  • 其中，\(w\) 是我们可控的部分。至于 \(x_i\) 到底是不是 iid 或者 zero-centered，其实也不好说

进一步，我们令 \(\Var(y_j) = \Var(x_i)\)，从而：\(\Var(w_i) = \frac 1 {Din}\)。从而，我们就可以把标准差设置为 \(\frac 1 {\sqrt{Din}}\)

  • 注意：这里的方差、期望值，就是 \(x_i\), \(y_j\) 本身。我们把它们视作随机变量。

Kaiming/MSRA Initialization

对于 ReLU 而言，我们就不能用 Xavier 初始化了。

我们需要把标准差设到 \(\frac 2 {\sqrt{Din}}\)。直观来说，这是因为 ReLU 削掉了一半。

Residual Network

image-20240323003541808

Regularization

Dropout

我们在训练的时候，可以为每一层设置一个 mask，s.t. 将被 mask 的 output 设置为 0，也就是 dropout

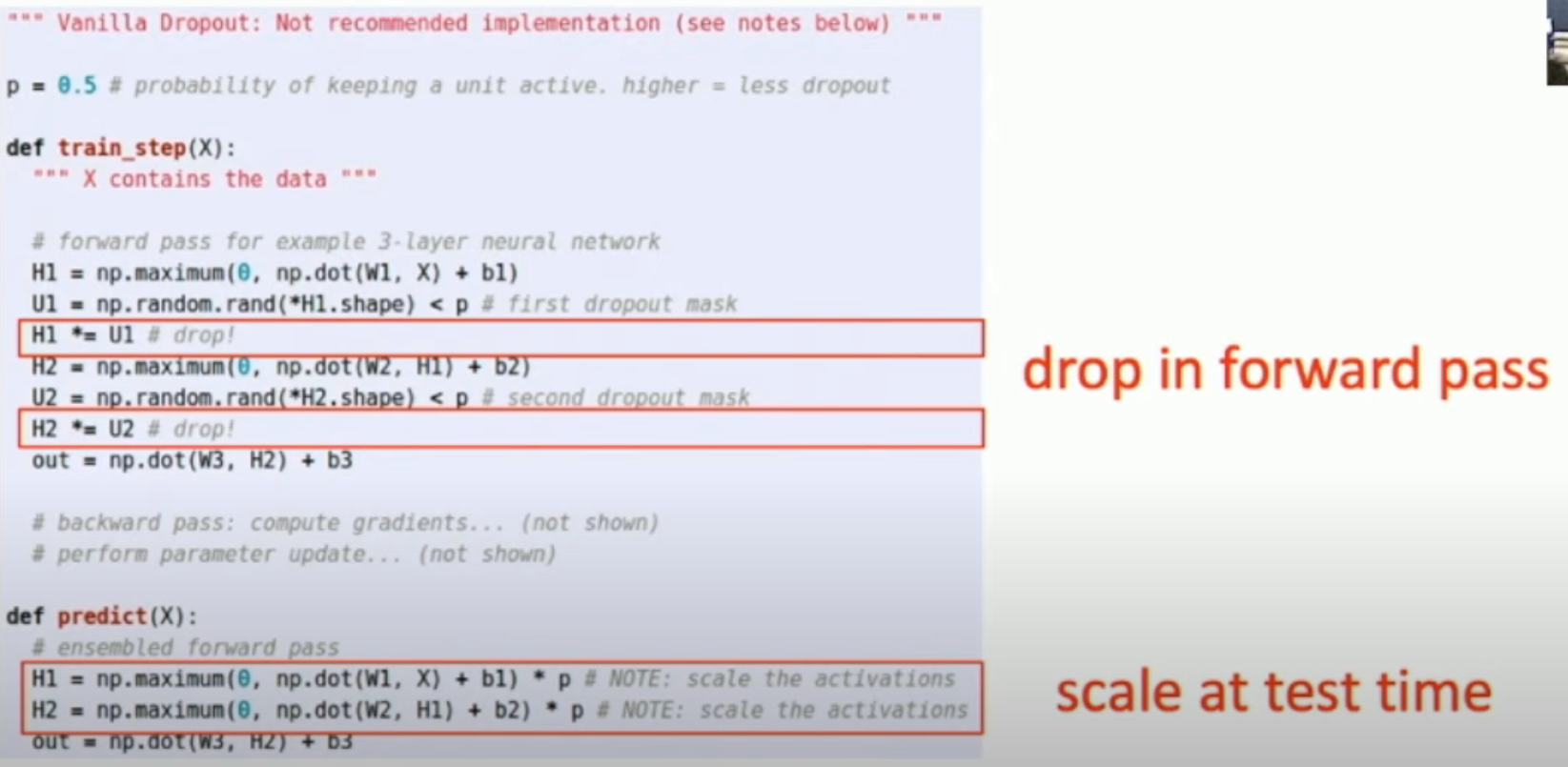
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(Wl, X) + bl) # Linear followed by ReLU
U1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= Ul # drop!

Dropout 的好处是：

  1. 避免 co-adaptation between outputs of the same layer（见下图）
  2. 某种意义上，相当于我们不训练整个网络，而是训练子网
    • 比如说，如果对 4096 全连接层进行 mask，一共可以有 \(2^{4096}\) 种 mask，每一个 mask 对应一个不同的子网。因此，dropout 就相当于我们每一次都在其中随机选择一个来进行训练。

image-20240323005027700

How to predict?

一、我们不希望在 predict 的时候出现随机性。因此，我们不可以在 predict 的时候又进行 random dropout。

二、同时，由于我们是在子网上 train 的（输出比全网小），因此，我们不能够直接使用我们的全网来进行 predict。一个直观的想法是：用“所有子网的加权平均”来 predict，也就是：

\[ y = f(x) = E_{z}[f(x,z)] = \int p(z) f(x,z) \mathrm dz \]

可惜，一共 \(2^{4096}\) 个子网，我们无法 naively 加权平均。

  • 注意，上图中，我们通过 mask 来参数化了子网：

image-20240323005439636

不过，我们可以做一个近似，也就是把所有输出乘以其 dropout probability。

  • 对于单独一层而言，这是精确的期望值。但是，对于多个 layers，由于有 ReLU 这样的 non-linear 的出现，因此就就只是一个近似而已。

也就是说：

image-20240323010538018

Variation of Dropout: Inverted Dropout

为了避免 scale at test time，我们可以在 drop 一部分参数的同时，同时 rescale 另一部分参数，如下图所示：

image-20240323011234332

我们在 drop val < p 的同时，将那些 val >= p 的 output scale 了 1/p。

Where to Insert The Dropout?

一般情况下，我们是在参数最多的层 insert the dropout。

Data Augmentation

我们可以通过 background knowledge，来为我们的数据集增加更多的数据，同时通过引入随机性，增加模型的 robustness，避免 overfitting。

具体的方法，比如说：随机的旋转、对称、剪切、改变亮度、增加透镜效果等等。

Random Crops and Scales

image-20240323025455703

如上，我们可以在

  • 训练的时候，将图片 randomly resize，然后 randomly sample a patch，作为 augmented training data
  • 测试的时候，我们就不能够这样 random 了。因此，我们指定了 5 个 scales，并且指定了剪裁位置，在保证测试结果的稳定性的同时，增加了测试的难度。

A General Concept of Regularization: Introducing Randomness

image-20240323020814856

如图：

  1. dropout 是以 mask 的形式，引入一个独立的 randomness
  2. batch normalization 中，由于我们每一次都抽取不同的 minibatches，因此相当于引入一个 training set 内部的 randomness
  3. 最后，两者都会 average out randomness
    • 前者是直接使用一个近似（上文说过）
    • 后者是在训练的时候，记录下来每一次的 normalization transformation，之后平均这些 transformations
  4. 另外，data augmentation 也是随机创造新的 augmented data，然后最后使用固定大小、位置的局部图片来测试

对于更加现代的网络架构，最后的全连接层被 global pooling 所取代，因此参数量大大减少，很多时候我们并不用 dropout。

Which Regularization You Should Use?

  1. Don't use dropout unless there are fully connected layer in your network
  2. Batch normalization and data augmentation are almost always good
  3. Try cutout (i.e. cut a piece of picture out) and mixup (i.e. use some random weight to mix up two pictures) esp. for small datasets (like CIFAR-10)

Also, don't forget the most basic, non-random L2 regularization, which you should almost always use.