Skip to content

Lec 4: Lambda Calculus

Recap: Evaluation

Operational semantics can be expressed as evaluation rules.

There are two kinds of rules: one is computation rule (shown below), which performs "real" computation steps.

image-20240307000619826

One is congruence rule (shown below), which determine where computation rules can be applied next.

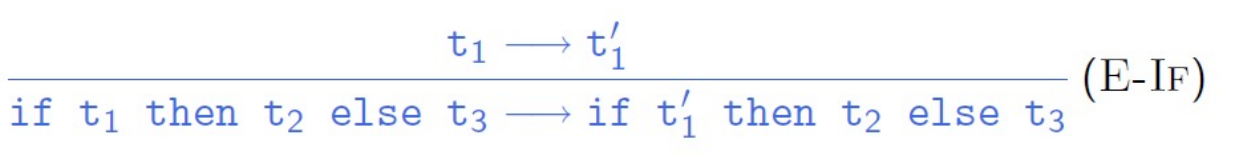
image-20240307000817153

Evaluation as Relation

Actually, the three rules above can be written as

image-20240307000936716

which means ((if true then t2 else t3), t2) and ((if false then t2 else t3), t3) are included in the relation set \(\to\), and if (t1, t1') belongs to \(\to\), ((if ...)) also belongs to \(\to\).

The Untyped Lambda Calculus

The syntax of lambda calculus:

image-20240307001553833

Syntactic Conventions

  • The λ-calculus provides only one-argument functions, all multi-argument functions must be written in curried style.

  • The following conventions make the linear forms of terms easier to read and write:

  • Application associates to the left e.g.,t u v means (t u) v, not t (u v)
  • Bodies of λ-abstractions extend as far to the right as possible e.g., λx. λy. x y means λx. (λy. x y), not λx. (λy. x) y

Free Variables

Free variables are variables that are not bounded by any \(\lambda \left<\text{name of the variable}\right>.\).

e.g. In \(\lambda x. \lambda y. x~y := \lambda x.(\lambda y. x~y)\), \(x\) is bounded (by \(\lambda x.\)); whereas in \(\lambda y. x y\), \(x\) is free.

Operational Semantics

Beta reduction is the only computation rule

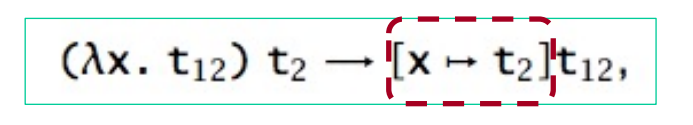
image-20240307002547505

  • the term is obtained by replacing all free occurrences of x in t12 by t2
  • a term of the form (λx.t) v — a λ-abstraction applied to a value — is called a redex (short for “reducible expression”).

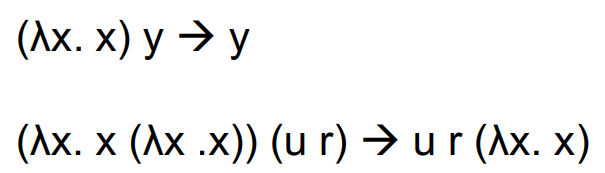
Examples: image-20240307002819496

Rules (for full-beta reduction strategy):

image-20240307005416846

Reduction Strategies

  1. Full beta-reduction: any redex may be reduced at any time.

image-20240307005849464

Note: lambda calculus is confluent under full beta-reduction. Ref. Church-Rosser property.

  1. The normal order strategy: reduce leftmost and outmost first, if no leftmost and outmost possible, do whatever you like~

image-20240307010001132

  1. Call-by-name strategy: a more restrictive normal order strategy, allowing no reduction inside abstraction.

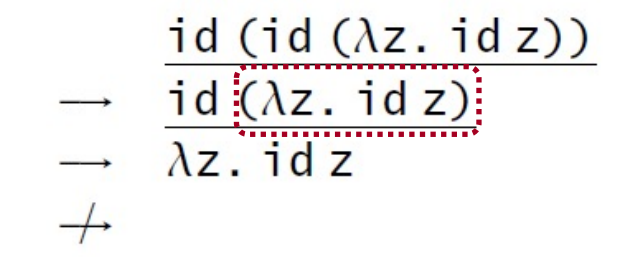
image-20240307010038036

stop before the last and regard \(\lambda z. \operatorname*{id} z\) as a normal form.

  1. Call-by-value strategy: only outermost redexes are reduced and where a redex is reduced only when its right-hand side has already been reduced to a value

image-20240307010328009

Programming in the Lambda Calculus