Skip to content
\[ \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bv}{\mathbf{v}} \newcommand{\dt}{\mathrm dt} \newcommand{\Dt}{\Delta t} \newcommand{\bxt}{\bx^t} \newcommand{\bxtt}{\bx^{t + \Dt}} \newcommand{\dbxtt}{\dot \bx^{t + \Dt}} \]

Lec 21-22: Animation

弹簧-质点系统（Mass Spring System）

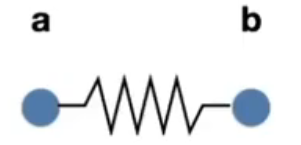
image-20240221133319789

对于如上的弹簧，我们考虑二阶力（弹簧势能）和一阶力（摩擦力）：

  • 二阶力

    \[ \begin{aligned} \mathbf f_{a \to b} &= k_s \frac{\mathbf {b-a}}{\lVert\mathbf{b-a}\rVert}(\lVert\mathbf{b-a}\rVert - l) =k_s \widehat{\mathbf {b-a}}(\lVert\mathbf{b-a}\rVert - l) \newline \mathbf f_{b \to a} &= -\mathbf f_{a \to b} \end{aligned} \]

  • 其中，\(l\) 是 rest length

  • 一阶力

    \[ \begin{aligned} \mathbf f_{b} = -k_d (\widehat{\mathbf {b-a}} \cdot (\mathbf{\dot b - \dot a}) )\widehat{\mathbf {b-a}} \newline \mathbf f_{a} = -\mathbf f_{b} \end{aligned} \]

  • 括号里就是 a, b 相对速度在弹簧方向上的大小。

例子：布料

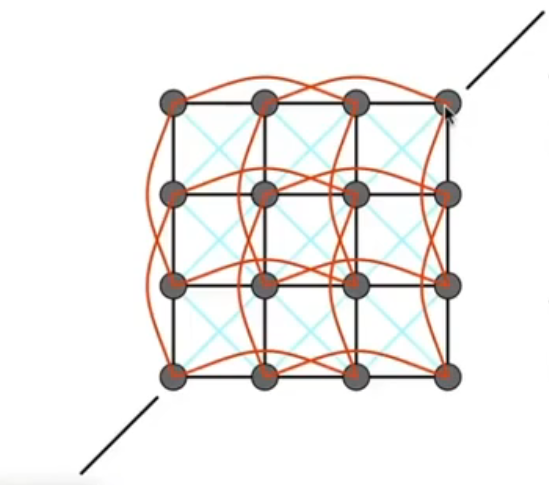
image-20240221140953108

如图，布料具有

  • （各向同性）抗剪切
  • 抗弯折

的特性。因此，横平竖直的弹簧系统肯定是不行的。

为了抗剪切，我们加入了对角线的弹簧；为了抗弯折，我们加入了 skip connection（也就是如图长度为 2 的长弹簧）。

从而，我们得到了可以近似模拟布料的 mass spring system。

粒子系统

我们可以将一个系统近似为粒子之间的相互作用。

每个粒子的运动都由一系列物理/非物理的力所决定。

It's a popular technique in graphics and games, in the sense that it's

  • Easy to understand, implement
  • Scalable: fewer particles for speed, more for higher complexity

but it does have challenges

  • May need many particles (e.g. fluids)
  • May need acceleration structures (e.g. to find nearest particles for interactions)

Particle System Animations

For each frame in animation

  • [If needed] Create new particles
  • Calculate forces on each particle
  • Update each particle’s position and velocity
  • [If needed] Remove dead particles
  • Render particle

Particle System Forces

Attraction and repulsion forces

  • Gravity, electromagnetism,
  • Springs, propulsion,

Damping forces

  • Friction, air drag, viscosity,

Collisions

  • Walls, containers, fixed objects,
  • Dynamic objects, character body parts,

例子：bird flock simulation (as ODE)

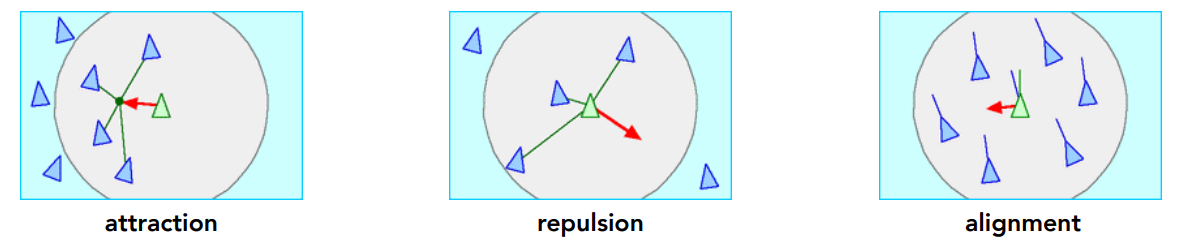
Model each bird as a particle Subject to very simple forces:

  • attraction to center of neighbors
  • repulsion from individual neighbors
  • alignment toward average trajectory of neighbors

image-20240221144137857

数值模拟——欧拉方法

欧拉方法很广，可以分为

  • 直接欧拉法（i.e. naive Euler method），\(\bxtt = \bxt + \bv(\bxt) \Dt\)

  • 中点法

    \[ \begin{aligned} \newcommand{\bxmid}{\bxt + \bv(\bxt)\Dt / 2} \bx_{mid} &= \bxmid \newline \bxtt &= \bxt + \bv(\bx_{mid}) \Dt = \bxt + \bv(\bxmid) \Dt \end{aligned} \]

  • 中点法很多情况下等价于一个抛物线

  • 隐式欧拉法

    通过求解方程（\(\bxtt\) 是未知数）

    \[ \begin{aligned} \bxtt = \bxt + \Dt ~\dbxtt = \bxt + \Dt ~\bv(\bxtt) \end{aligned} \]

    我们可以通过牛顿迭代法等方法求出 \(\bxtt\) 的值

  • 通常，隐式欧拉法比直接（显式）欧拉法更加稳定

  • Runge-Kutta Families

这是一系列高阶优化方法的集合，很适合用作非线性的情况。