Skip to content

Lec 20: Color and Perception

光谱

Spectral Power Distribution (SPD, 谱功率密度)

单位：

  • radiometric units / nanometer (e.g. watts / nm)
  • can also be unit-less
  • 这种情况下，就是相对密度（相对于最大值）

例子

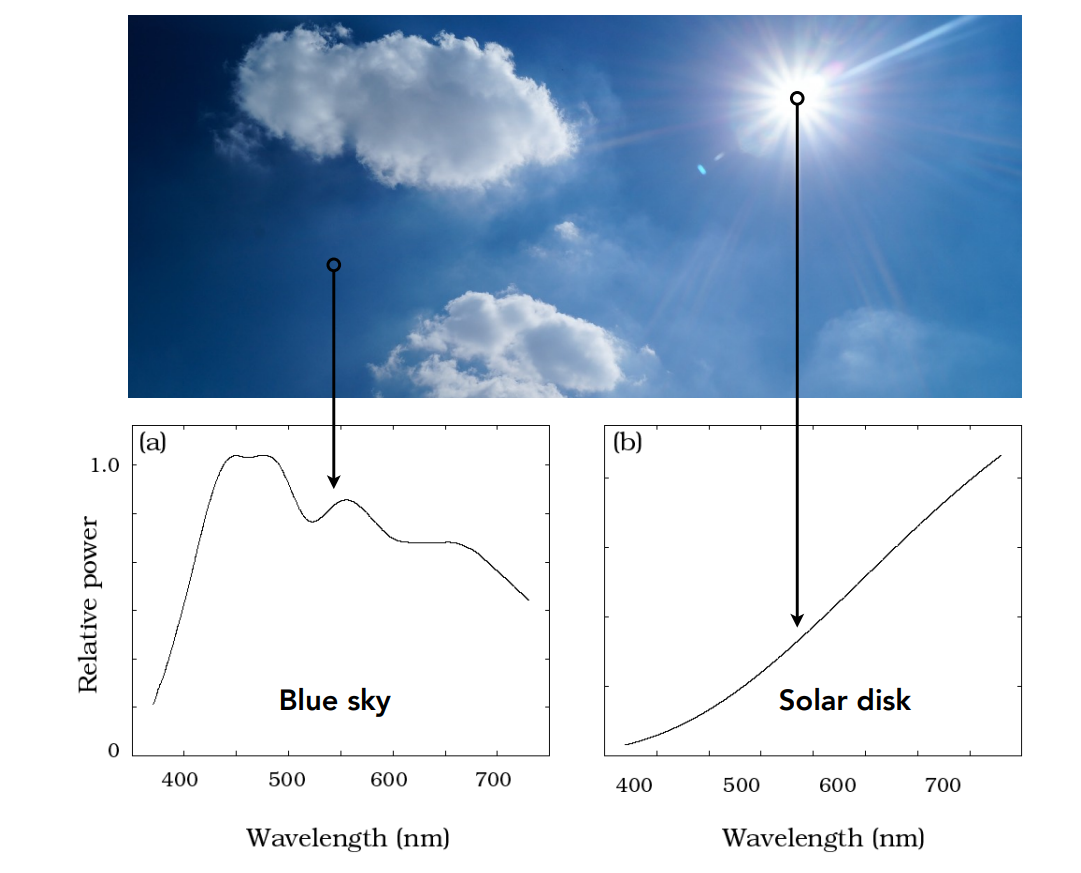
image-20240219113855501

注意：此处只考虑可见光段

颜色

人类通过三种视锥细胞对光线进行感知。视锥细胞对光线的感应强度如下：

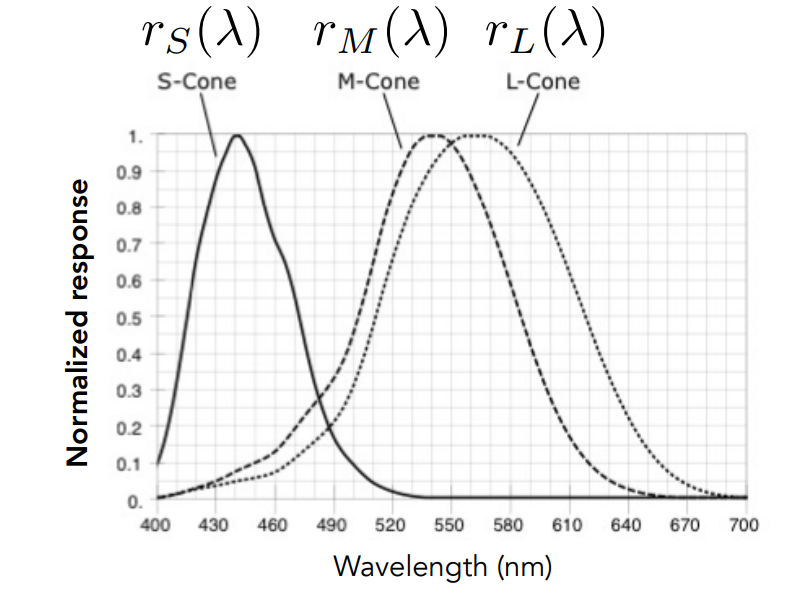
image-20240219120803091

也就是说： $$ \begin{align} S &= \int r_S(\lambda)s(\lambda) \mathrm d \lambda \ M &= \int r_M(\lambda)s(\lambda) \mathrm d \lambda \ L &= \int r_L(\lambda)s(\lambda) \mathrm d \lambda \ \end{align} $$ 从而，我们感知的颜色，就是从无穷维光谱（i.e. \(\left\{ s \middle | s: \mathbb R^+ \to [0,1] \right\}\)）到三维响应（i.e. \(\left\{(S,M,L) \middle | S,M,L \in [0, +\infty) \right\}\)的一个线性映射。

Metamerism（同色异谱）

显然，不同的光谱，在人眼中，可以是同一颜色。

事实上，由于响应只有三维，我们可以使用三种预先调配好的颜色的线性组合，来组合出所有可能的颜色。

RGB 系统

RGB 使用单色光（可以理解为 delta 函数），分别是：

  • R (Red): 700 nm
  • G (Green): 546.1 nm
  • B (Blue): 435.8 nm

给定任意波长，我们需要通过下列混合方式，来得到这种颜色（注意部分区域为负数）：

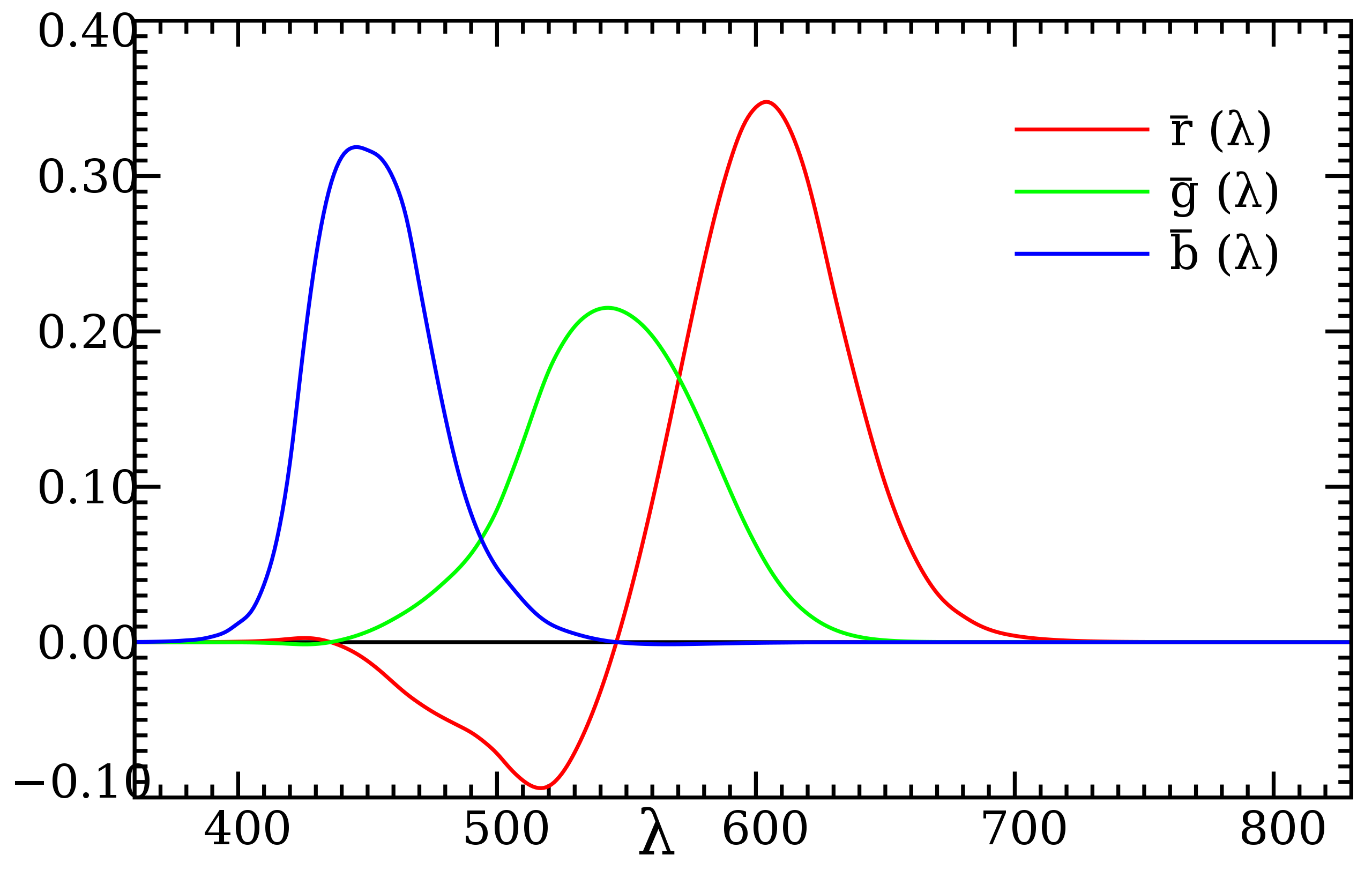
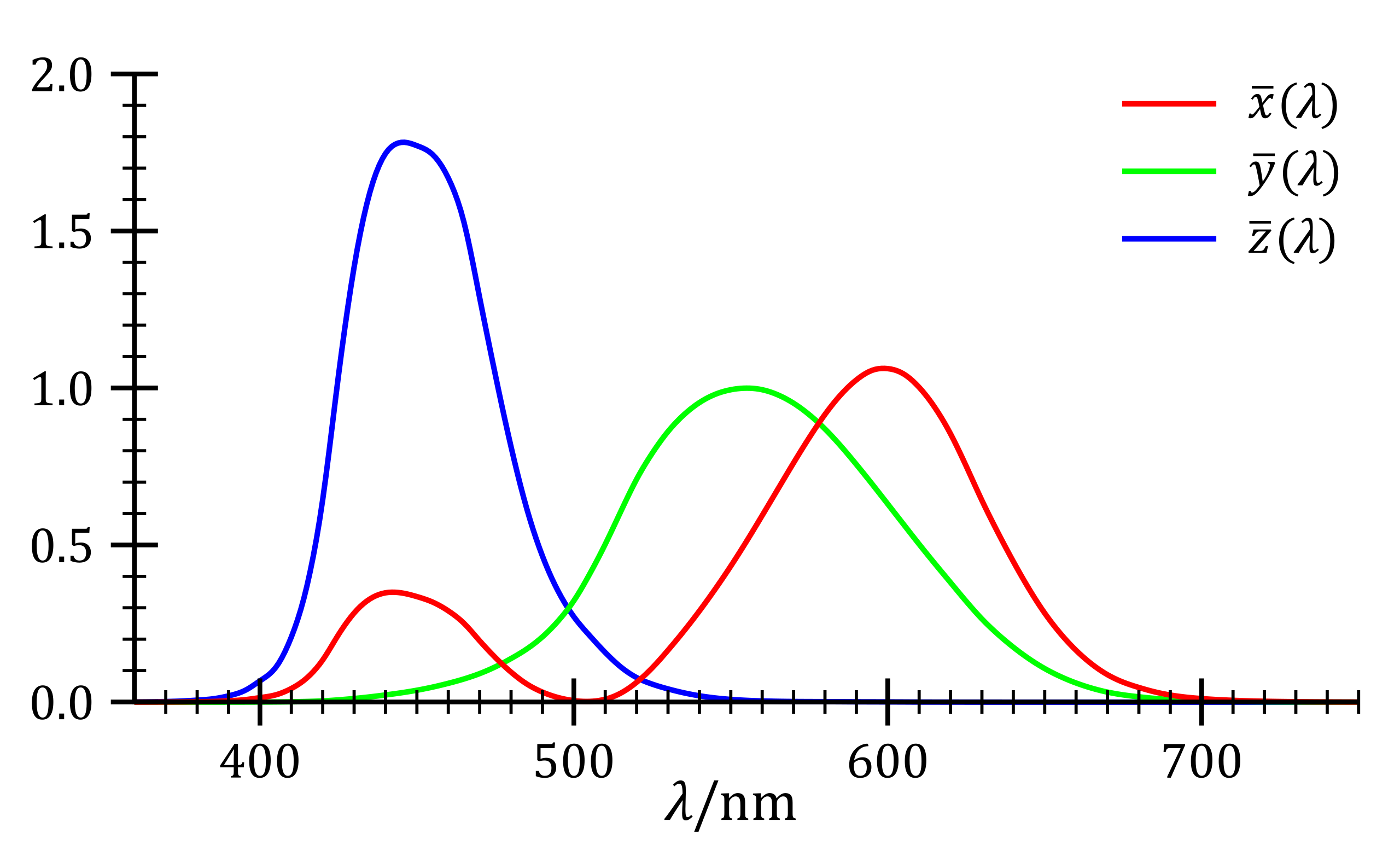
undefined

从而，对于含有任意频谱的光线，我们采用以下积分，来计算该光线所需的 R, G, B： $$ R_{\mathrm{CIE~RGB}} = \int _ { \lambda } s(\lambda) \bar r(\lambda) \mathrm d \lambda \ G_{\mathrm{CIE~RGB}} = \int _ { \lambda } s(\lambda) \bar g(\lambda) \mathrm d \lambda \ B_{\mathrm{CIE~RGB}} = \int _ { \lambda } s(\lambda) \bar b(\lambda) \mathrm d \lambda $$

  • 注意用的是 \(\overline {r,g,b}\) 曲线，而非 \(r, g, b\) 曲线

XYZ 系统

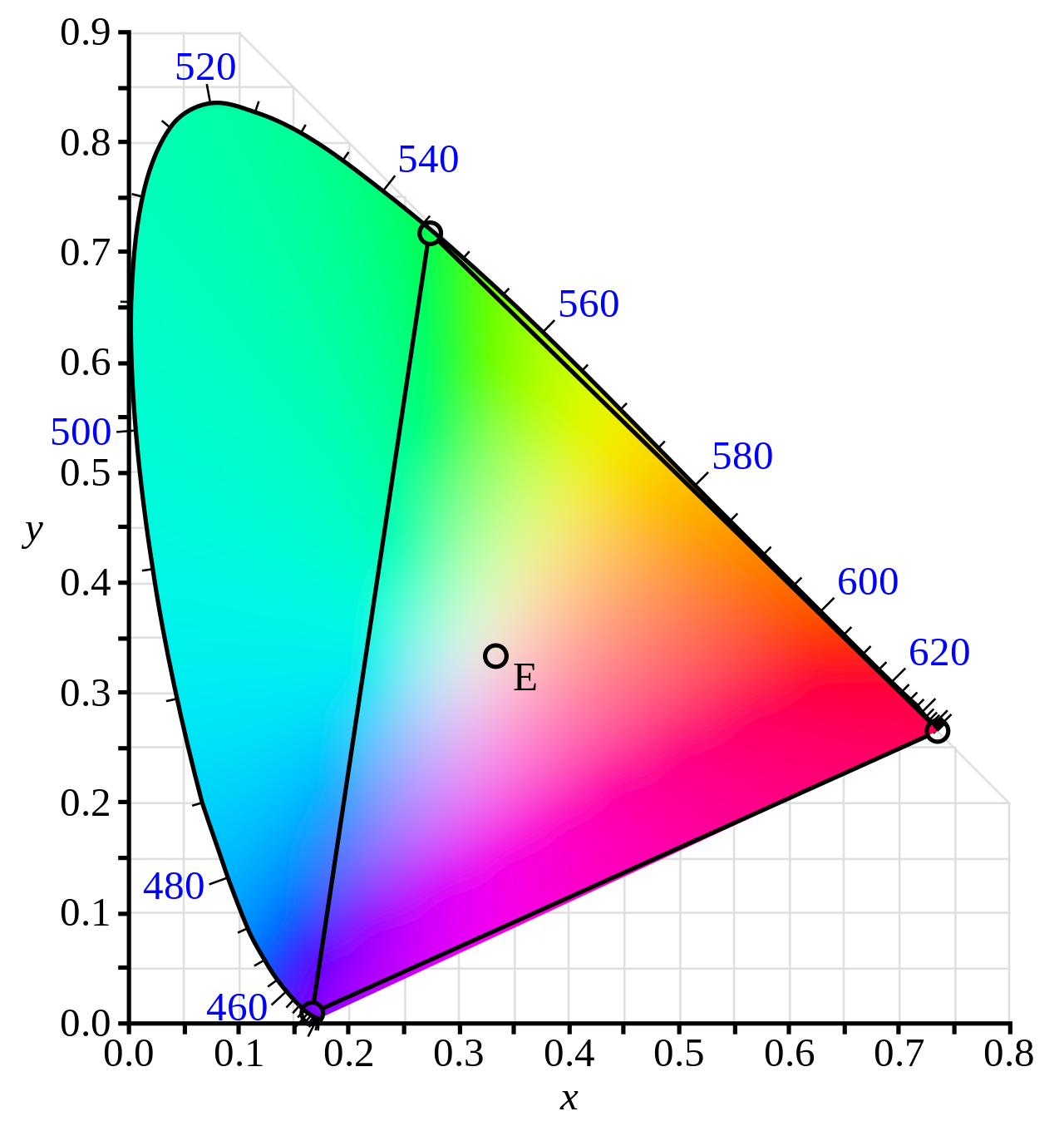
我们为了避免出现负数，对 RGB 系统做了一个线性变换，从而得到了 XYZ 系统。

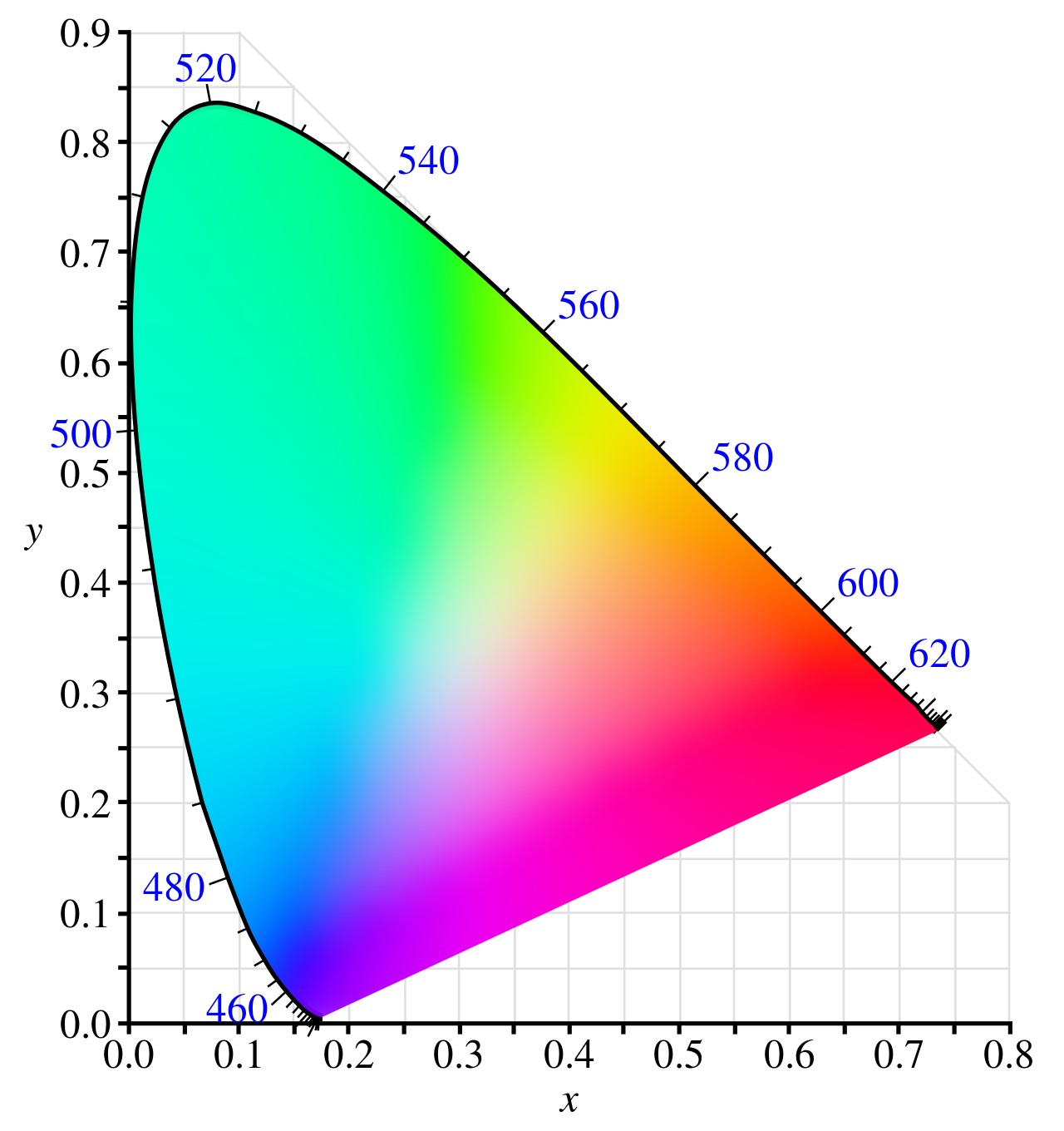
undefined

undefined

如图，RGB 色彩区域在 XYZ 中的显示如下：

undefined