Skip to content

Lec 19: Cameras, Lenes and Light Fields

Field of View (FOV)

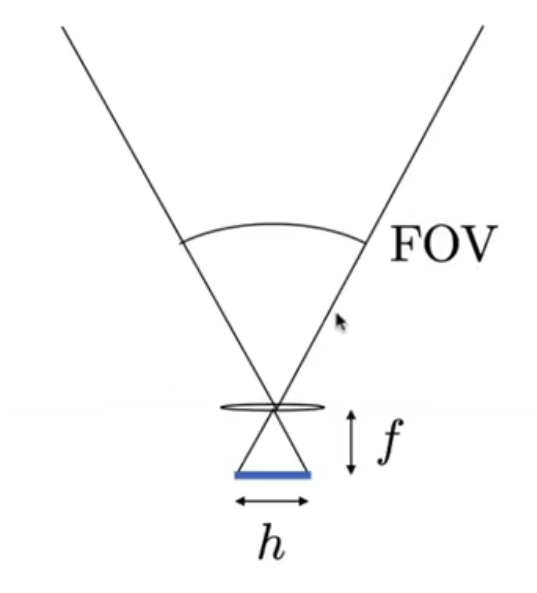
image-20240204105634894

如图，给定

  • 传感器的尺寸
  • 焦距

就可以算出 SOV：\(SOV = 2 \arctan{\left(\frac h {2f}\right)}\)

Focal Length

按惯例，给定传统的 35mm-format film (36 x 24mm)，SOV 和焦距就可以一一对应：

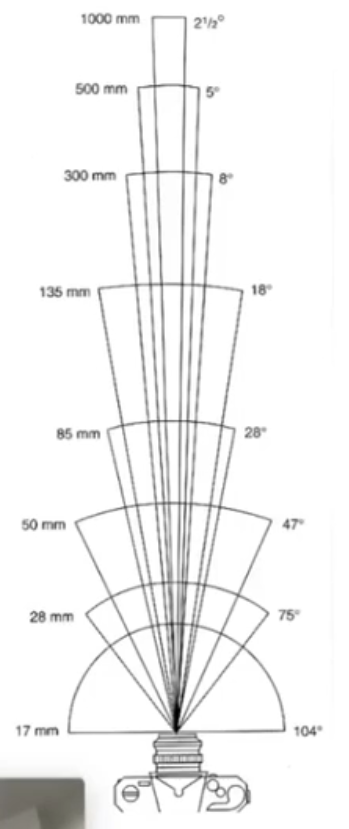
image-20240204110131467

因此，给定（标准尺寸下的）SOV，就能换算出焦距。

不过，相同焦距，尺寸越大，SOV 就越大。

Exposure

曝光 \(H = T \times E\)，也就是 Exposure = Irradiance x Time

  • 除此之外，还有一个 ISO。可以认为是后期处理，也就是放大

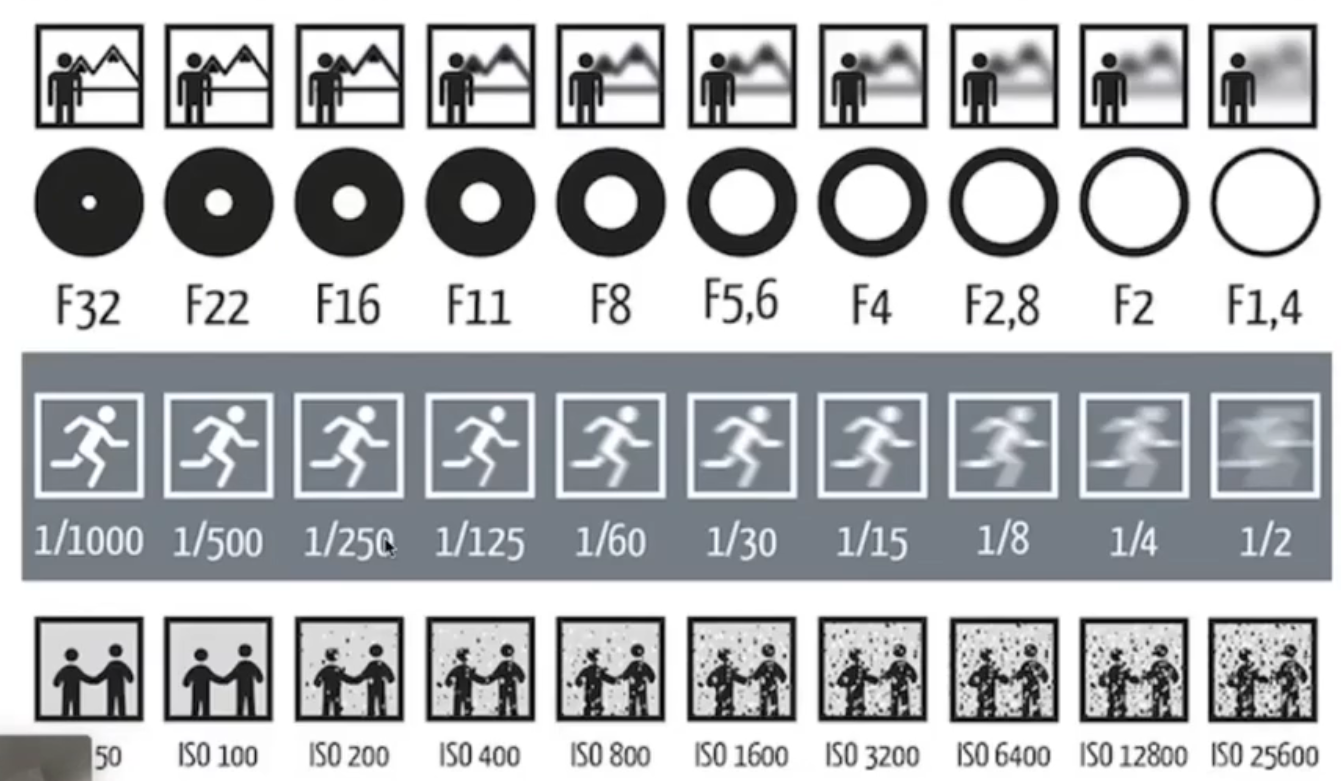
image-20240204112230344

如图，

  • 光圈越大（i.e. 直径越小），背景越锐利
  • 曝光时间越长，越虚+越亮
  • ISO 越大，越亮+绝对噪声越大

Circle of Confusion

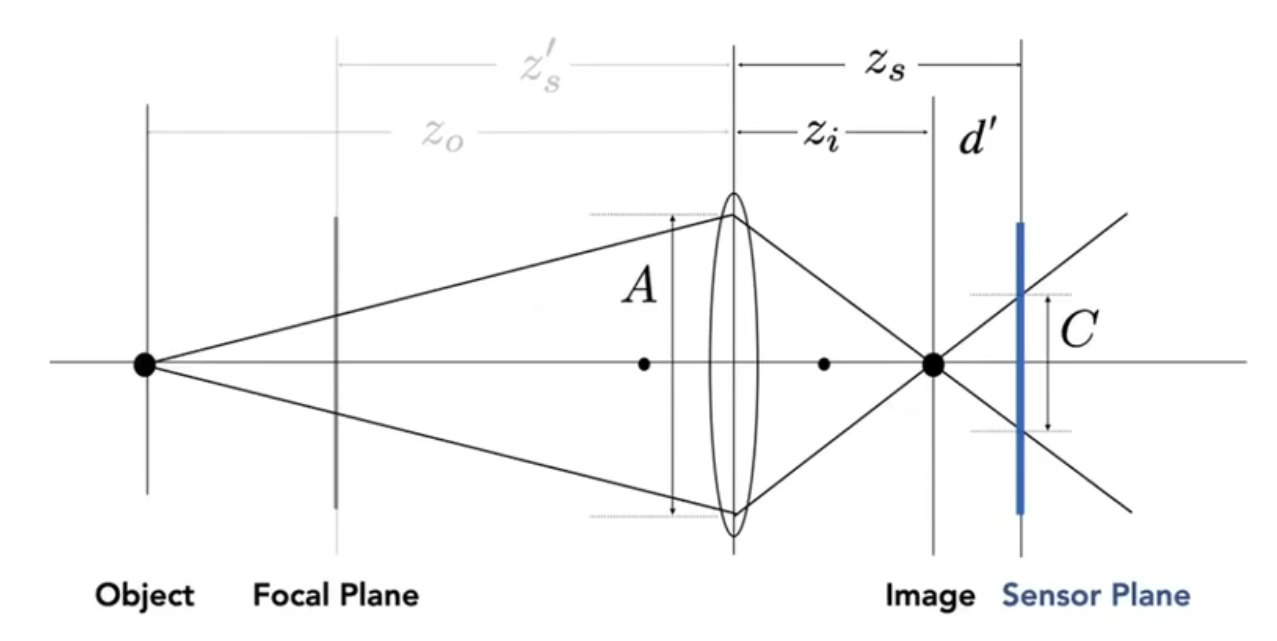
image-20240218190656411

如图，给定

  • 物距
  • 焦距
  • 像距

由 $$ \frac 1 {z_o} + \frac 1 {z_i} = \frac 1 {z_s'} $$ 我们就可以求出 circle of confusion 的相对大小 $$ \frac C A = \frac {d'} {z_i} = \frac {z_s - z_i} {z_i} = \abs{z_s - z_i} (\frac 1 {z_o} - \frac 1 {z_s'}) $$ 对于固定的 \(z_s, z_o, z_s'\)，\(A\) 越小，\(C\) 就越小，从而 \(z_o\) 的变化范围可以更大一些，也就是景深更大。

Depth of Field

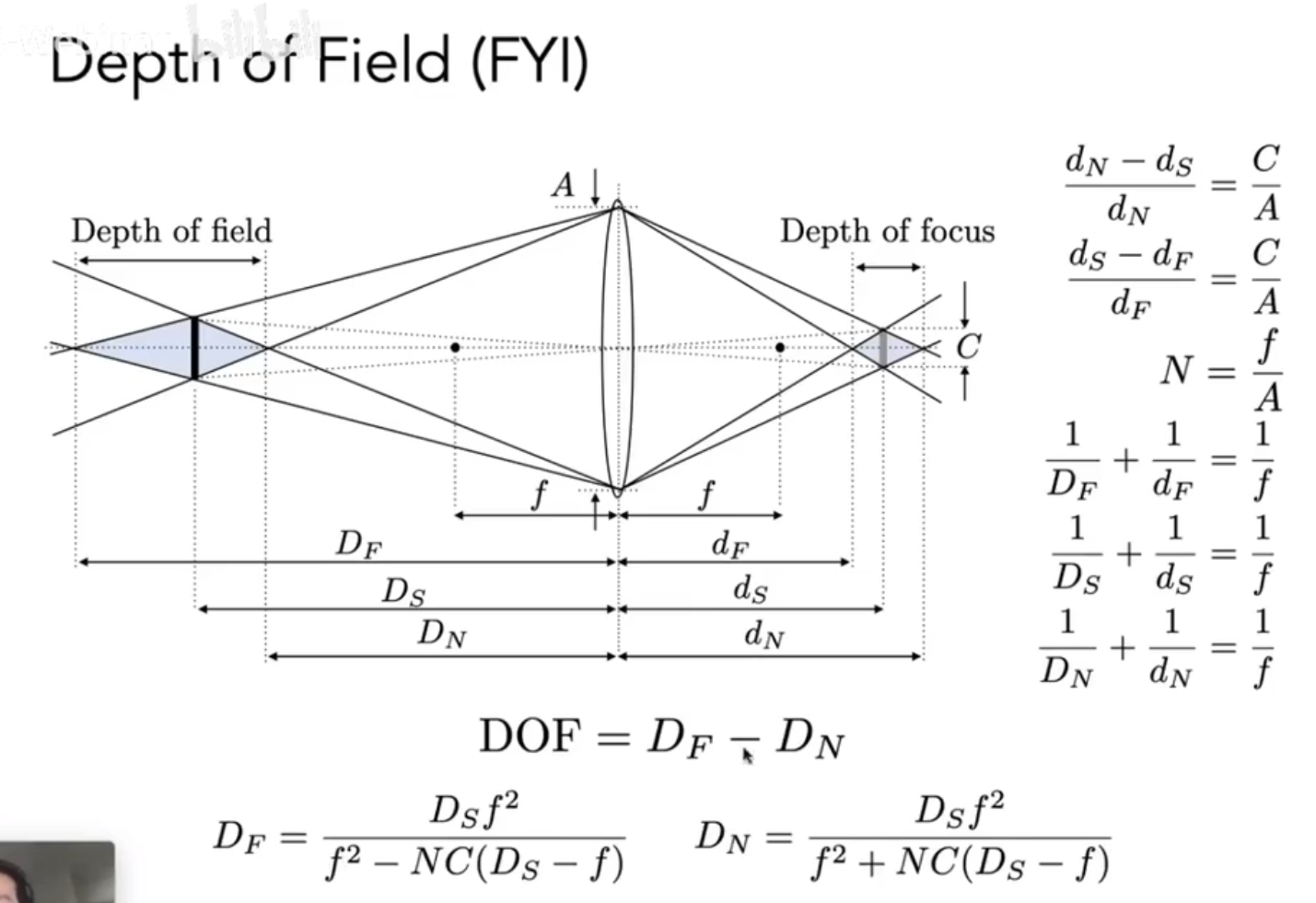
image-20240218192231184

如图，在镜头、场景固定的情况下，景深取决于 \(C\) 的最大值。我们通过这些量求出 \(D_F\) 和 \(D_N\)，从而求出景深。

Light Field/Lumigraph（光场）

全光函数

image-20240205175255449

如图，如果我们记录

  • 所有位置（i.e. \((V_x, V_y, V_z)\)）
  • 所有方向（i.e. \((\theta, \phi)\)）
  • 所有波长（i.e. \(\lambda\)）
  • 在所有时刻（i.e. \(t\)）

sensor 接受的 intensity，那么，这就可以完整描述我们的 visual reality。

4D 光场和 Lumigraph

我们不妨将光场中的 \(t\) 和 \(\lambda\) 去除，并且只关心某一个平面上的光场，从而，我们只需要

  • 所有位置（i.e. \((V_x, V_y)\)）
  • 所有方向（i.e. \((\theta, \phi)\)）

也就是 4 维。

进一步，我们不妨利用两个相互平行的平面来进行参数化（如下图），从而更加 practical。

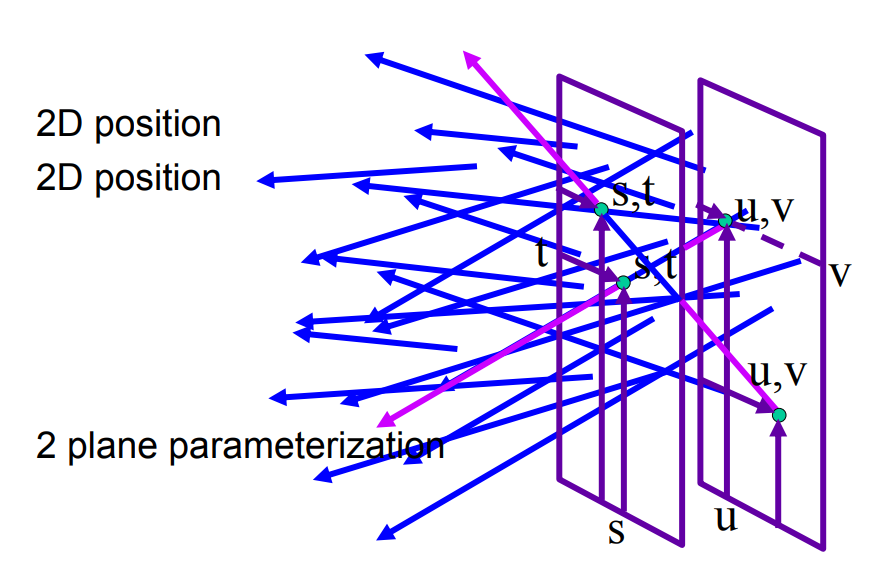
image-20240219104052206

例子

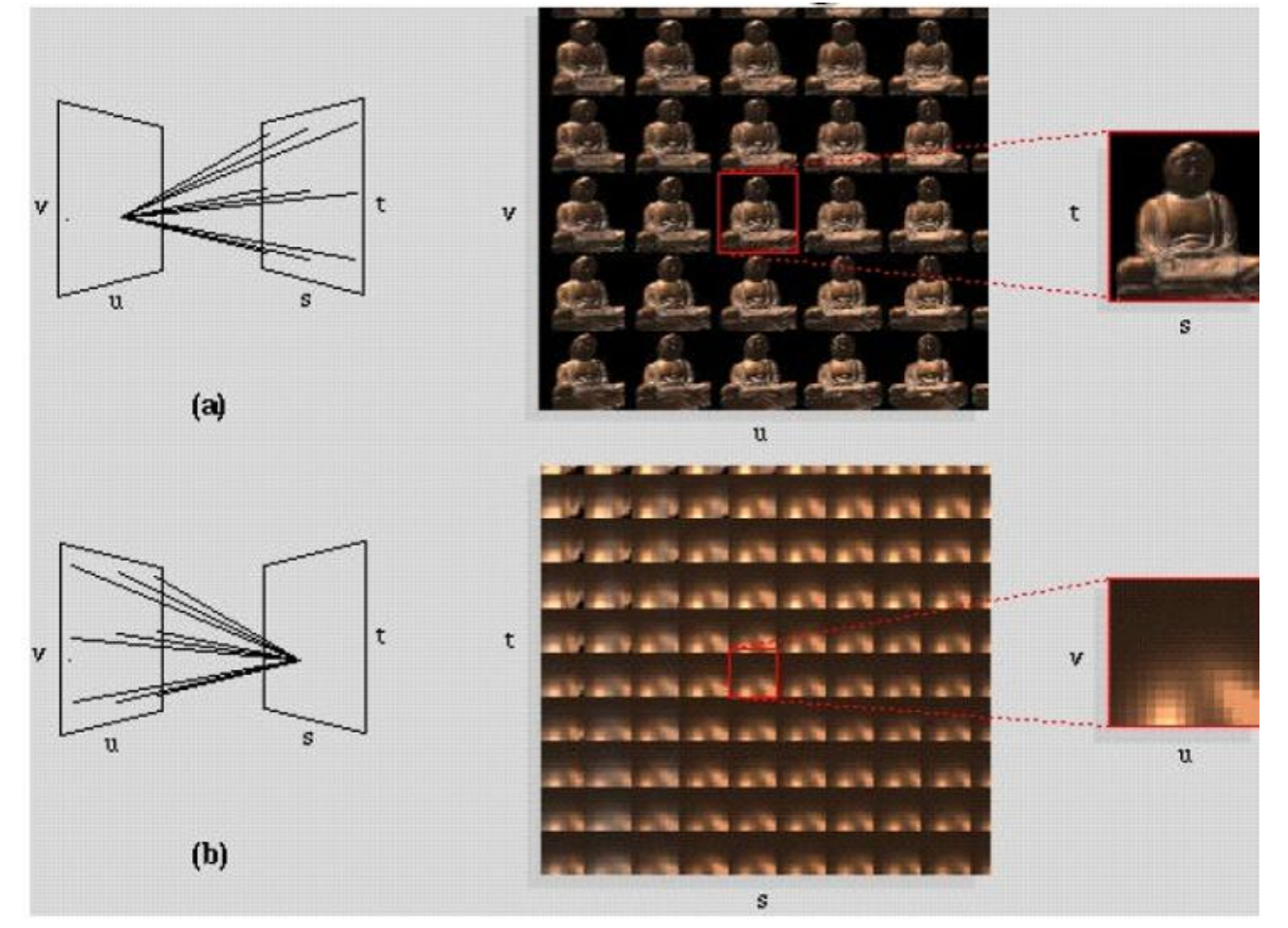
image-20240219104225288

如图，

  • 从 u-v 平面看向 s-t 平面，每个 u-v 平面的像素都记录了从 s-t 平面各个像素发出的光（也就是 u-v 平面的像素记录了各个方向的光）。
  • u-v 平面上，像素点 \((u_0, v_0)\) 记录的图片可以理解为函数 \(i_{u_0, v_0} (s,t) = f(u_0, v_0, s,t)\)
  • 从 s-t 平面看向 u-v 平面，每个 s-t 平面的像素记录了应该往 u-v 平面各像素发出的光。
  • s-t 平面上，像素点 \((s_0, t_0)\) 记录的图片可以理解为函数 \(j_{s_0, t_0} (u,v) = f(u, v, s_0, t_0)\)

因此，使用照相机阵列，我们可以获取各个 \(i_{u_0, v_0}(s,t)\)，进而可以转换成各个 \(j_{s_0, t_0} (u,v)\)，用作之后的显示。

光场照相机

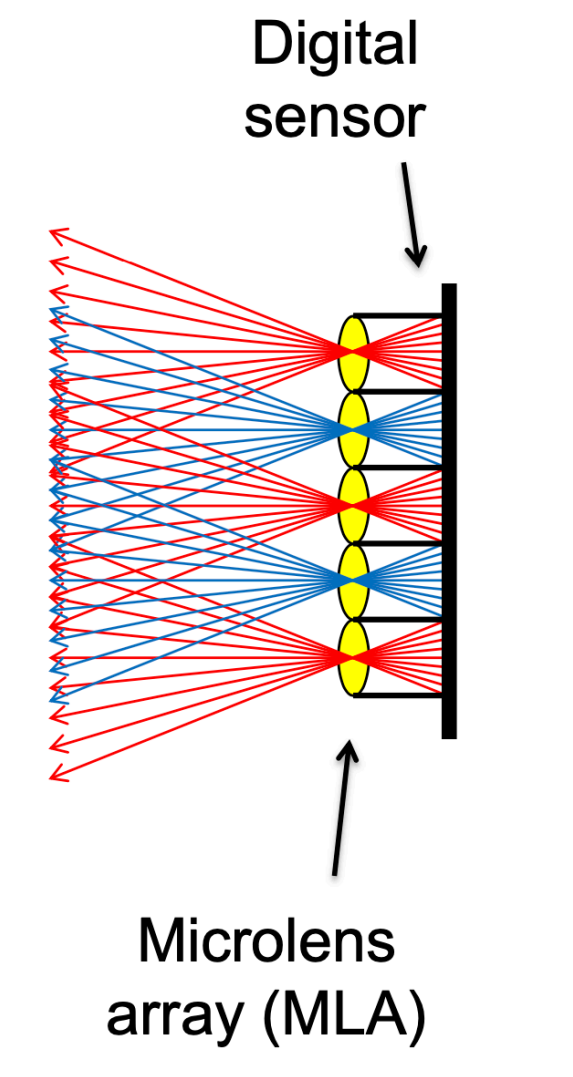
image-20240219110046036

如图，原本的一个像素接受到的就是 irradiance（i.e. 所有方向上光的加权平均）。 我们现在将这个（父）像素“拆开”成若干子像素，从而每个子像素记录了父像素的某个方向上的 radiance。

从而，我们可以获取各个 \((u_0, v_0)\) 的 \(i_{u_0, v_0}(s,t)\)。

这样，我们可以利用这个细节丰富的图像（也就是上面例子中的图 (a)），还原出 \(f(u,v,s,t)\)，从而在后期进行任意的调位置、调焦、调光圈操作。

例子

如果我们希望获得针孔摄像机+斜下方的视角，我们只需选取所有斜向上的光线即可。

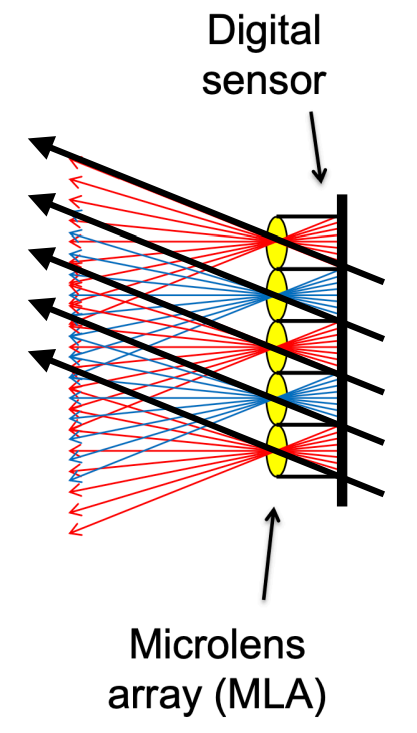
image-20240219112030530

对于其它位置，同理。

对于调焦、光圈，我们只需要计算出底片上每个像素接收到的光线（利用 \((u,v,s,t)\) 参数化），然后把 \(f(u,v,s,t)\) 加权平均即可。

In all, all these functionalities are available because

  • The light field contains everything

Any problems to light field cameras?

  • Insufficient spatial resolution (same film used for both spatial and directional information)
  • High cost (intricate designation of microlenses)
  • But anyway, Computer Graphics is about trade-offs