Skip to content

Lec 17: Materials and Appearances

Diffuse/Lambertian Material

对于漫反射的材质而言，其遵循 Lambert's Cosine Law，也就是其 radiant intensity 在不同的立体角上不一样： $$ I_\theta \sim \cos \theta $$ 从而，其所有方向的 radiance 都相同（也就是说，人眼从任何方向看过去，亮度都一样）： $$ L_\theta = \frac{\mathrm dI_\theta}{\mathrm dA \cos \theta} \equiv C $$ 我们如何计算一个材质的 BRDF 呢？

首先，由于漫反射性质，所有角度出射的 radiance 都必须相同。从而，无论怎样改变 \(\omega_o\)，\(f_r(\omega_i, \omega_o) \equiv \text{constant}\)。另外，由于所有入射光线都对出射没有影响，所以进一步，改变 \(\omega_i\)，也是常数。从而，\(f_r(\omega_i, \omega_o)\) 就是常数。

其次，不妨假设四面八方的相同强度的光线照射一个漫反射物体，从而，由于能量守恒，物体也必须反射那么多的光线。因此所有角度入射、出射的 radiance 均相同。通过积分： $$ \begin{aligned} L_o(\omega_o) &= \int_{H^2} f_r L_i(\omega_i) \cos \theta \mathrm d\omega_i \ &= f_r L_i \int_{H^2} \cos \theta \mathrm d\omega_i \ &= f_r L_o \int_{H^2} \cos \theta \mathrm d\omega_i \ &= \pi f_r L_o \end{aligned} $$ 从而，\(f_r = \frac 1 \pi\)。

对于一般情况，能量可能不守恒。此时我们定义反射率 \(\rho\)，从而得到最终的 Lambertian BRDF： $$ f_r = \frac \rho \pi $$

  • 另外，\(\rho\) 可以是 \([0,1]\) 内的一个数，也可以是一个向量——分别对待三原色。

Glossy Material

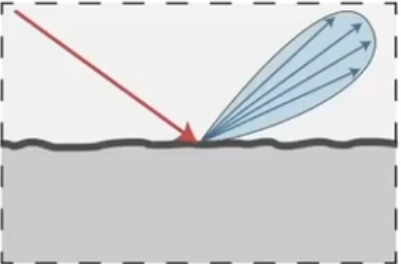
就是有一点镜面，但是不那么镜面的材质。如下图所示：

image-20240129222719670

Ideal reflective / refractive material (BSDF)

image-20240129223251738

对于反射而言，可以通过下图的方式计算

  • 出射光线的向量 \(\omega_o\)
  • 出射光线的方位角 \((\theta_o, \phi_o)\)

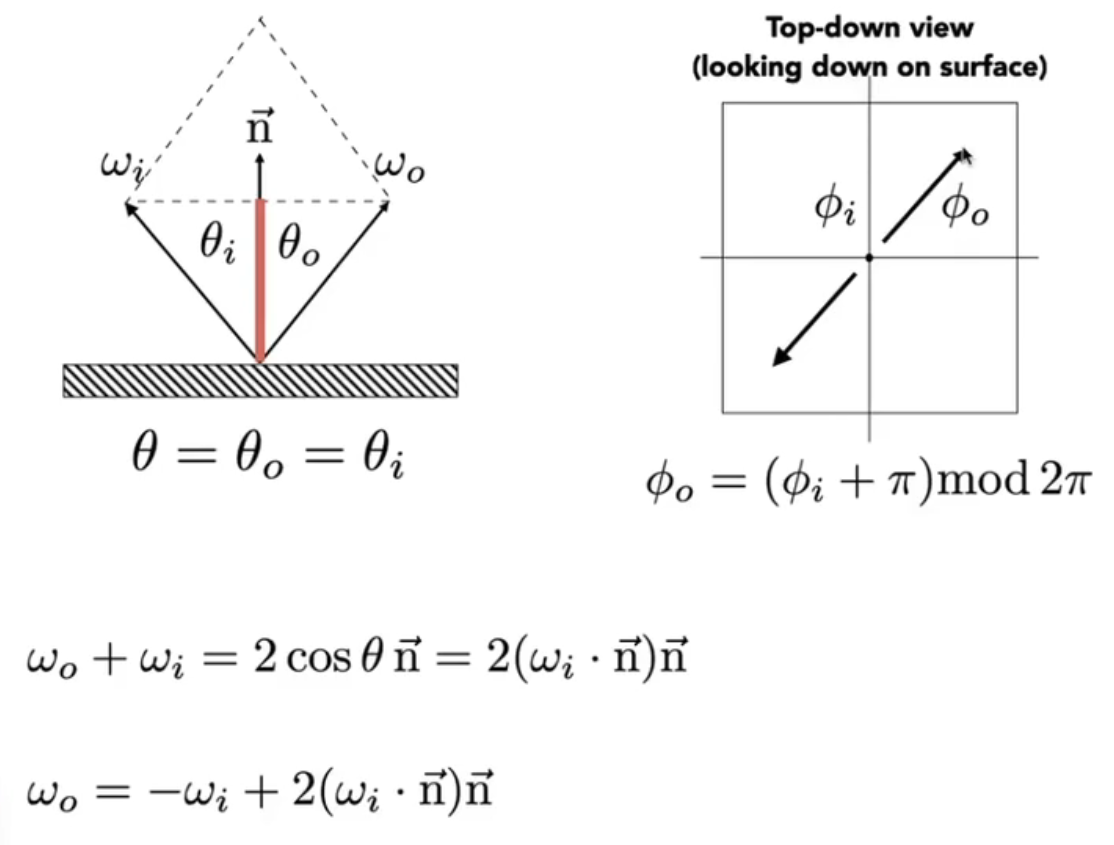
image-20240129225926690

另外，反射的 BDRF 是 Dirac 函数： $$ f_r(\omega_i, \omega_o) = \rho * \delta(\theta_o - \theta_i) \delta ((\phi_o + \pi - \phi_i) \operatorname{mod} 2\pi) $$

  • 其中 \(\rho\) 还是反射率

  • 对于镜面，我们肯定就不用 (Monte-Carlo) path tracing 的方法了（不考虑浮点数的精度，理论上方差无限大）。我们直接检测对应入射光方向的光线强度即可。BDRF 就是形式而已。

折射光也同理：

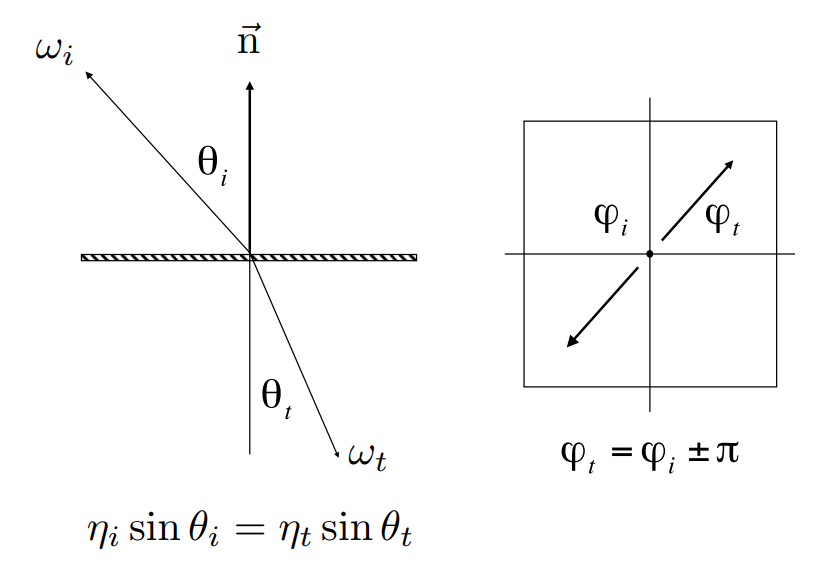
image-20240129231114833

同时，一定要注意全反射的情况。也就是当 \(\eta_t< \eta_i\) 的时候，如果 \(\sin {\omega_i} \geq \frac {\eta_t} {\eta_i}\)，那么就会发生全反射。此时我们只考虑反射，而不考虑折射。

最后，反射是 BR(eflexive)DF，折射是 BT(ransmittance)DF，反射和折射合起来并称 BS(cattering)DF。

Fresnel Reflection/Term

对于不同的角度，表面上折射和反射的光线的占比不同。

image-20240129233549971

image-20240129234147830

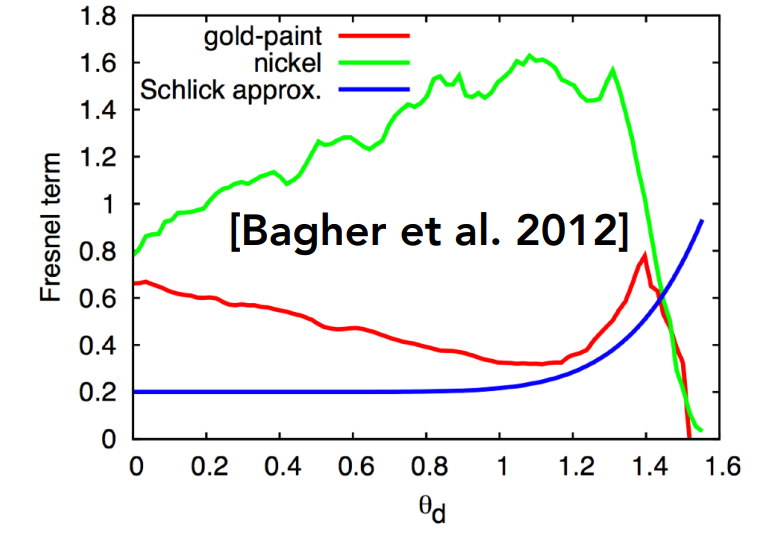
如图，金属（导体）的反射光占比一直比较高，而绝缘体的变化较大。

Schlick 近似结果见下图。可以发现不论对于绝缘体还是导体，近似效果都不错。

对于只包含反射和折射的表面： $$ \begin{aligned} f_s(\omega_i, \omega_o) = &\rho_{reflection} * F(\theta) * \delta(\theta_o - \theta_i) \delta ((\phi_o + \pi - \phi_i) \operatorname{mod} 2\pi) \ + &\rho_{refraction} * (1 - F(\theta)) \delta ( \theta_o + \arcsin(\frac{\eta_i}{\eta_t}\sin\theta_i ) - \pi) \delta ((\phi_o + \pi - \phi_i) \operatorname{mod} 2\pi) \end{aligned} $$

微表面模型

Motivation

从远处看一个表面，你看不见细节。你可以把它当成一个具有一定粗糙程度的平面。

Theory

对于一个 rough surface

  • Macroscale: flat & rough - 没有几何属性的粗糙材质
  • Microscale: bumpy & specular - 有几何属性的光滑材质

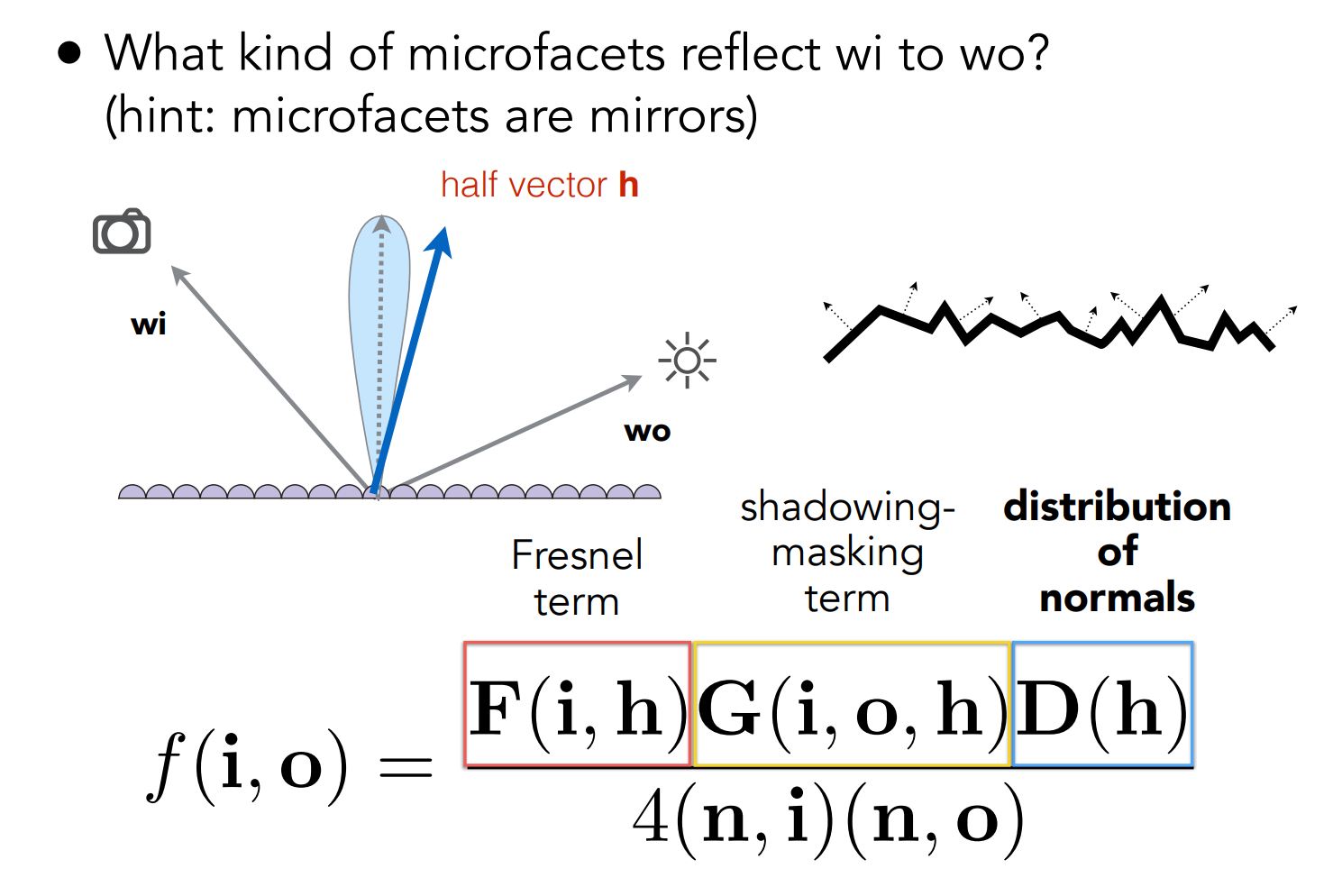
image-20240130013432418

其中

  • \(F(i, h)\) 是菲涅尔项，代表不同程度的反射
  • \(G(i,o,h)\) 代表 shadowing 和 masking 造成的损失
  • \(D(h)\) 是法线分布。需要满足归一条件：\(\int_{\Omega^+} D(h) (h \cdot n) \mathrm d \omega(h) = \int_0^{2\pi}\int_0^{\frac \pi 2} D(\theta, \varphi) \cos \theta (\sin \theta \mathrm d\theta \mathrm d\varphi) = 1\)
  • 和 BRDF 的积分式类似

Isotropic / Anisotropic Materials

image-20240201210639693

如图，各项同性（isotropic）的表面和各向异性（Anisotropic）的表面对于光线的反应是很不同的。

各项异性，使用 BRDF 的语言来说，就是 reflection depends on azimuthal angle（方位角）\(\phi\)。

即： $$ \exists \theta_i,\phi_i, \theta_r,\phi_r, \Delta \phi: f_r(\theta_i,\phi_i;\theta_r,\phi_r) \neq f_r(\theta_i,\phi_i + \Delta \phi;\theta_r,\phi_r + \Delta \phi) $$

  • 也就是说，BRDF 不是以法线为轴旋转对称的。
  • 从微表面的角度考虑，可以认为各向异性微表面一般就是法线分布不旋转对称

测量 BRDF

由于物理模型和真实情况有时候大相径庭，

image-20240201220307930

因此，在一些情况下，实际测量 brdf 还是有必要的。

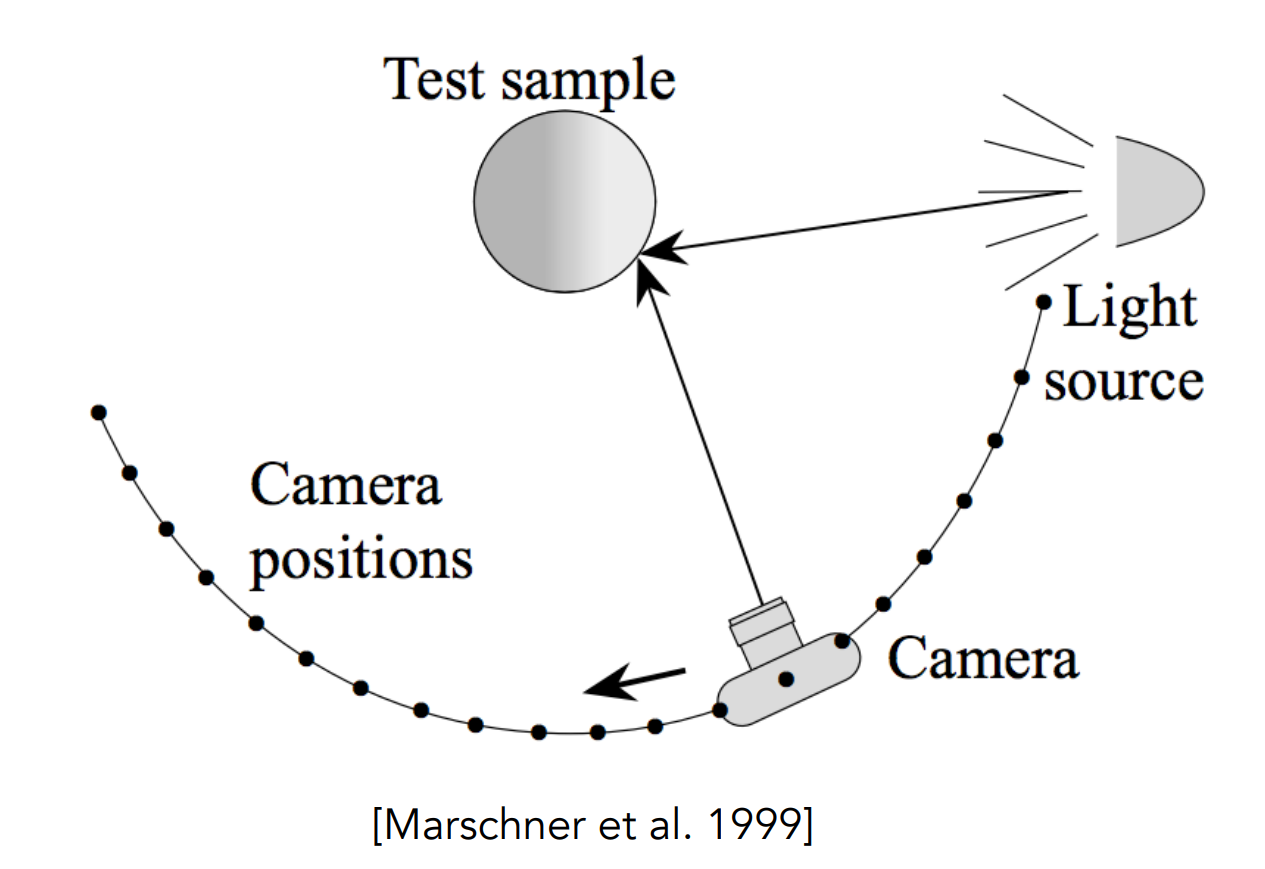
image-20240201220235342

一般地，普遍采用 gonioreflectometer 进行测量。

image-20240201220440088

采用表格进行储存。

image-20240201220426015

  • 对于各项同性的材质，储存量可以少很多。
  • 比如，对于 resolution 为 1 degree 的 table，如果是各向异性材质，那么就需要 90 * 90 * (360 * 361 / 2) = 90 * 90 * 180 * 361 个浮点；如果是各向同性，就只需要 90 * 90 * 180。
  • MERL BRDF Database 是很著名的开源 database
  • 具体地，每种材质的 brdf table 是 35 MB。算了一下，每个 unit 需要 24 bytes，也就是 3 个 double。也许是三原色分别？