Lec 13: Ray Tracing 1

光栅化的局限性

如图，假如使用光栅化实现上面的三个效果，实际上都不太好。

为什么使用光线追踪？

我们可以认为：

光栅化就是一种快速但是低质量（i.e. 很近似）的渲染技术。
光线追踪是一种很慢但是非常逼真的渲染方法

因此，

光栅化一般用于实时渲染，如游戏
光线追踪一般用于离线制作，如电影
后者往往要用到上万 CPU hours 去渲染 one frame

光线追踪基础

三个假设

光线沿直线传播
光线互不相干
光路可逆

Whitted-Style Ray Tracing

基本原理：

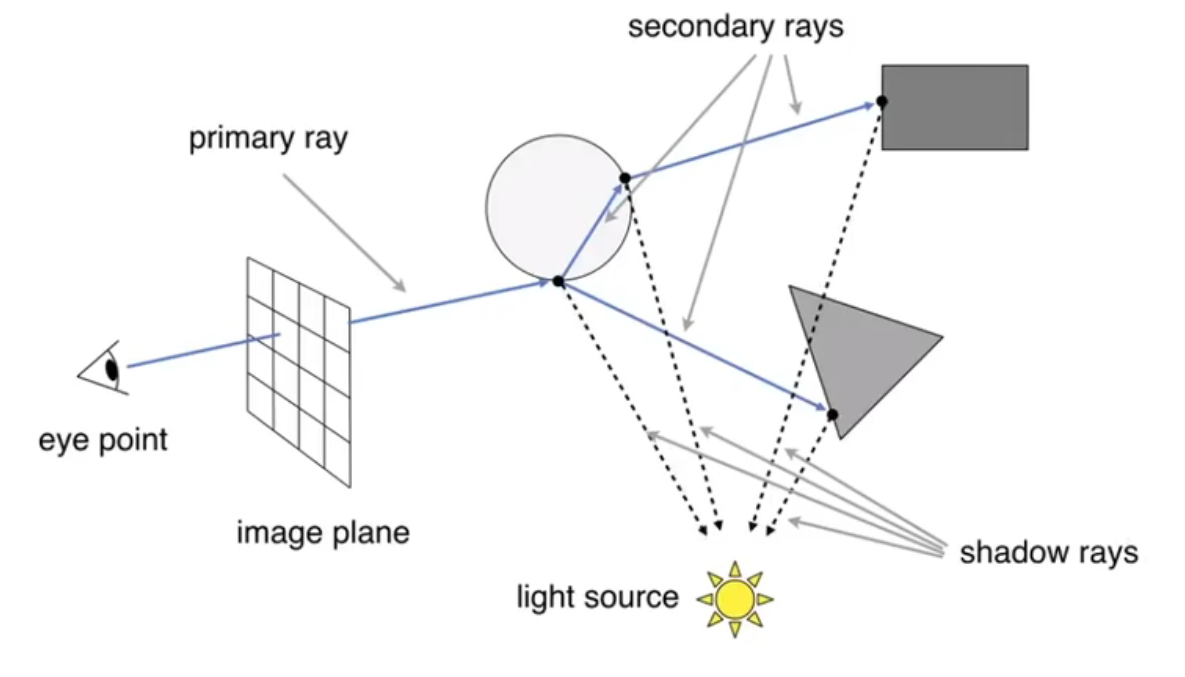
如图，利用光路可逆的原理，我们从眼睛出发，并不断在物体上进行反射和折射。

我们将反射和折射的点（也就是图中所有的 rays 的终点）利用 Blinn-Phong 模型算出光照强度，并加权（根据折射/反射的次数算出能量损失）求和，得到 primary ray 的终点处的总强度。然后进行渲染。

几何体求交

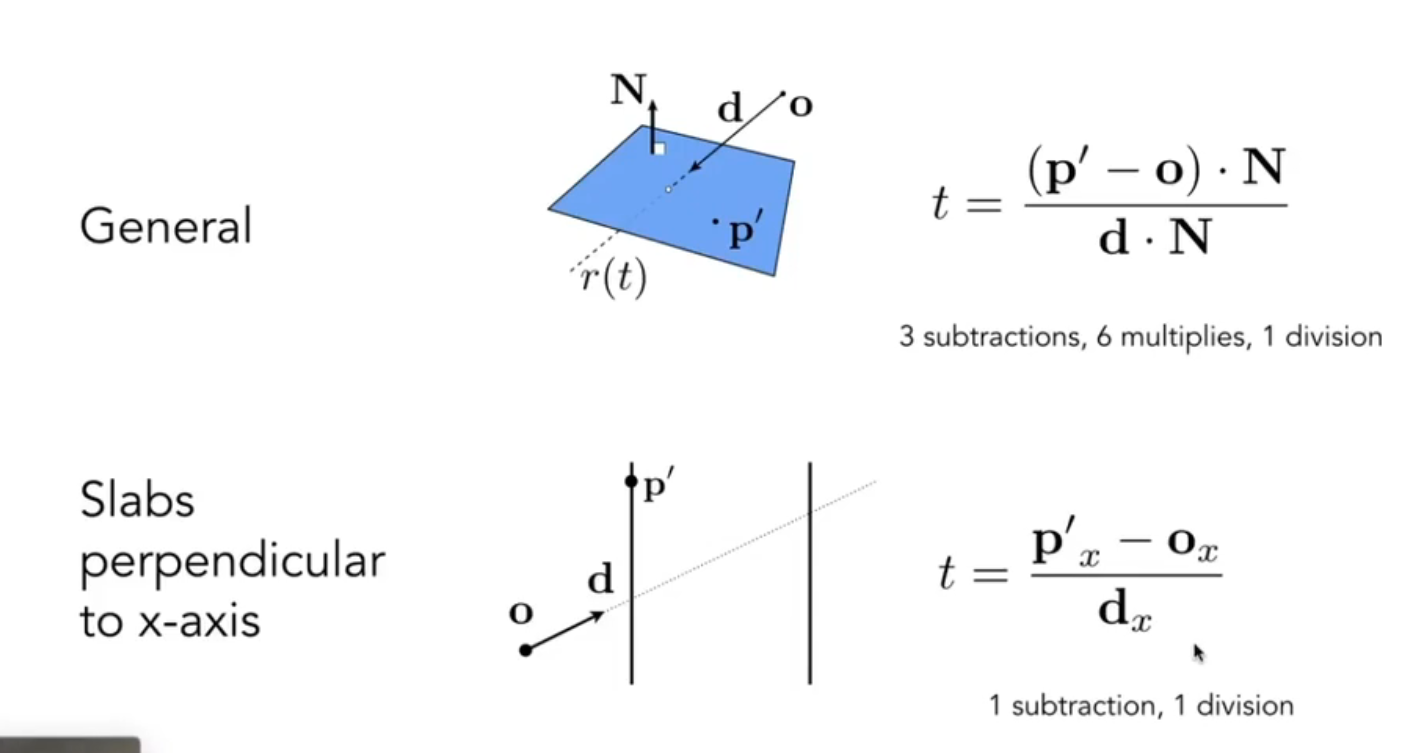
假设光线从 $\mathbf O$ 处，以方向 $\mathbf D$ 发射出去，则光线的方程为： $$ \mathbf{r}(t) = \mathbf{o} + t\mathbf{d}, \quad 0 \leq t < \infty $$ 与圆 $(\mathbf c, R)$求交： $$ (\mathbf o + t \mathbf d - \mathbf c)^2 = R^2 $$

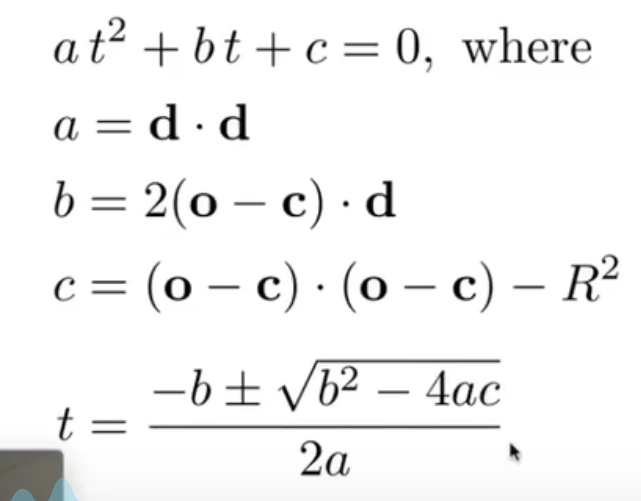
与三角形求交时，我们先求出三角形所在平面 $(\mathbf n, \mathbf p)$，其中，$\mathbf n$ 是法向量，$\mathbf p$ 是平面上一点。再求出光线与平面的交点。最后判断交点是否在三角形内部。

或者也可以用 Moller Trumbore 算法，使用三角形重心坐标，一步到位：

具体推导：方程可以简化为 $$ \begin{aligned} \mathbf D t + (\mathbf P_0 - \mathbf P_1) b_1 + (\mathbf P_0 - \mathbf P_2)b_2 = \mathbf P_0 - \mathbf O \ \begin{bmatrix} \mathbf D & -\mathbf E_1 & -\mathbf E_2 \end{bmatrix} \begin{bmatrix} t \ b_1 \ b_2 \end{bmatrix} = -\mathbf S \end{aligned} $$

通过 Cramer 法则，就可以得到最终的结果。

Note：$\det \begin{bmatrix} \mathbf A & \mathbf B & \mathbf C \end{bmatrix} = (\mathbf A \times \mathbf B) \cdot \mathbf C$

我们只需要判断是否有 $t \geq 0$ 且 $b_1, b_2 \in \left[0,1\right]$ 即可。

相交检测：Bounding Volume

对于观察者而言，如果对于每一个像素，我们追踪的光线都要和场景内所有的三角形进行相交检测，那么，总共的检测数量就是 # of pixels * # of meshes (* # of bounces，i.e. 光的反射次数 + 1)。

对于 # of meshes 数量庞大的情况，这是不可接受的

Bounding Volume（包围体积）

使用简单的形状包围物体。检测光线碰撞时，如果光线没有和包围体积发生碰撞，则不可能和内部的 meshes 发生碰撞。从而简化大量不必要的计算。

光线碰撞计算

对于包围体积的三对面，我们分别计算其进入时间和离开时间（不考虑进入和离开的位置）。以 2D 为例，如图：

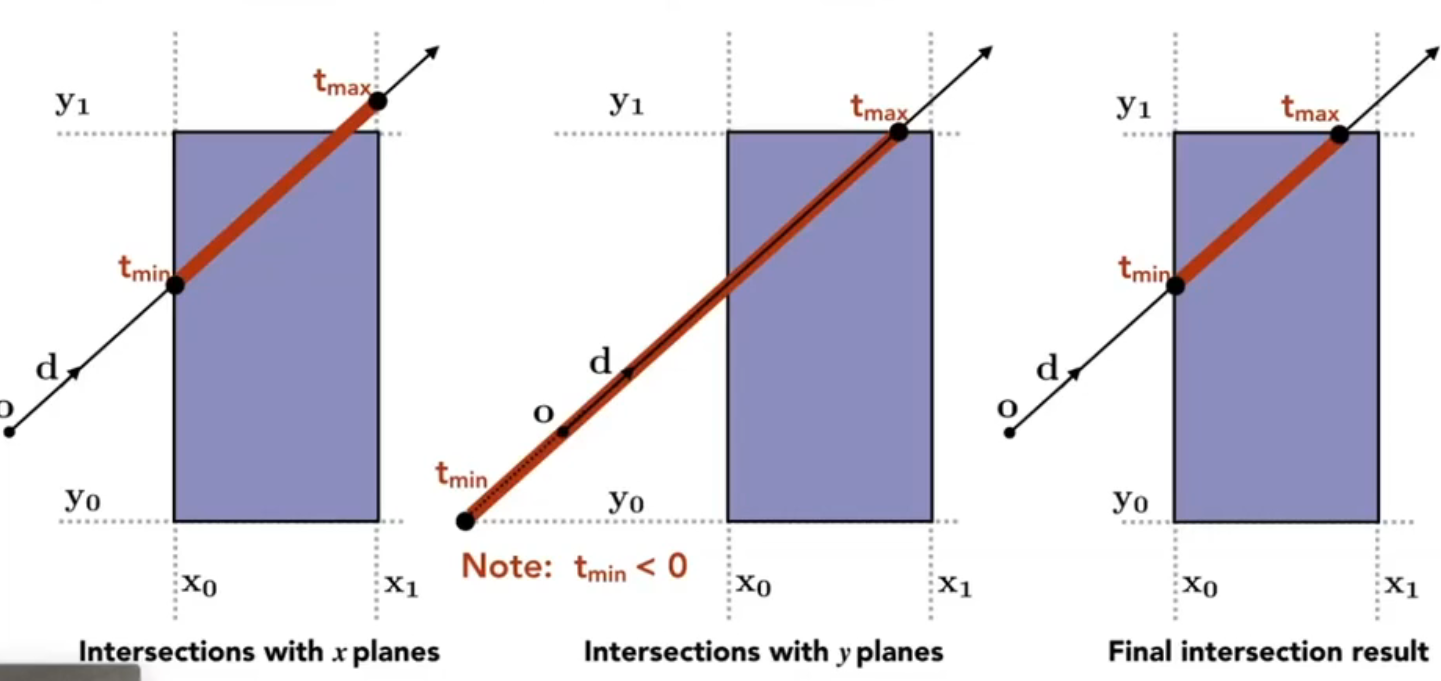
Generally speaking,

若：

$t_{exit} < t_{enter}$，则显然不对，实际上无交点
$(t_{enter}<)t_{exit} < 0$，则物体在光线背后相交，不成立
$t_{enter}<0\leq t_{exit}$，则光线本身从物体内部发出来，可行

因此，我们光线碰撞的充要条件：$t_{enter}<t_{exit}$ 且 $t_{exit} \geq 0$

Why AABB (Axis-Aligned Bounding Box)?

使用 Axis-Aligned 的方法，可以简化 $t$ 的计算，如下图所示：