Lec 12: 几何(进阶)¶
Mesh Subdivision: upsampling¶
网格的细分。

我们希望将粗糙的网格,细分成更加精细的网格。
Loop Subdivision¶
步骤:
- Split each triangle into four

-
Assign new vertex positions according to weights
-
new/old vertices are updated differently
更新算法:
-
新节点
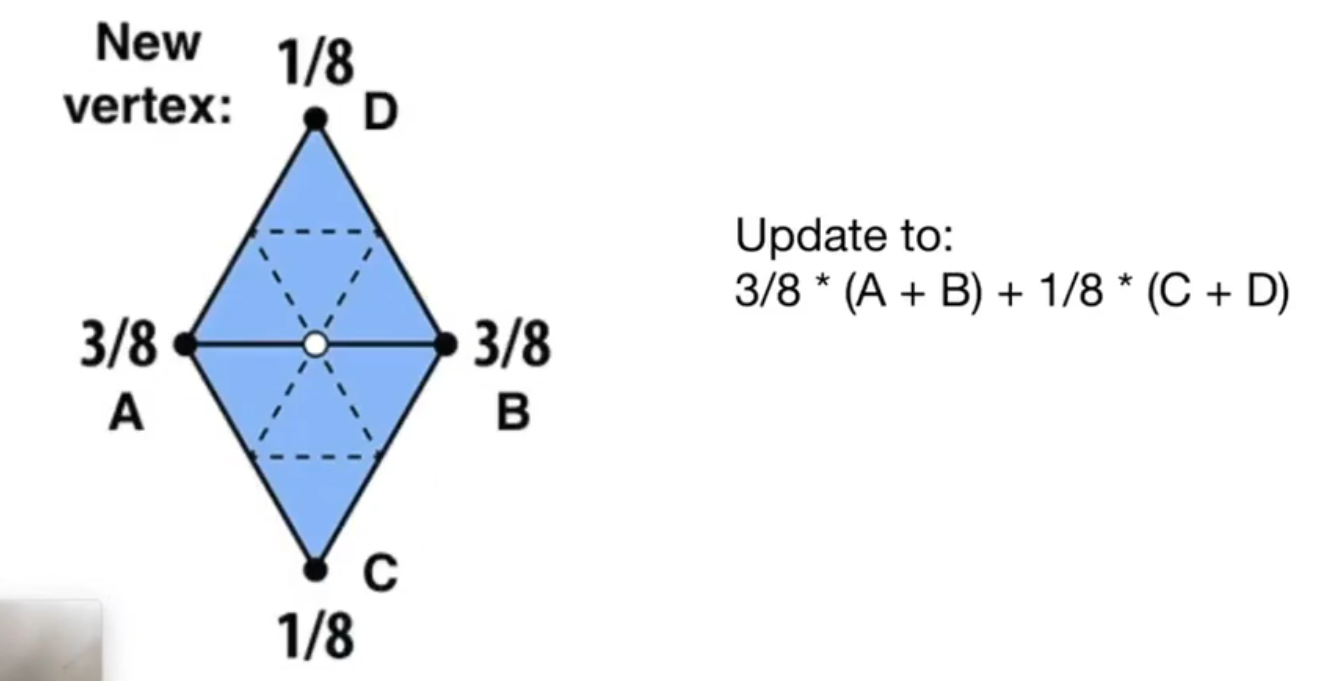
-
老节点
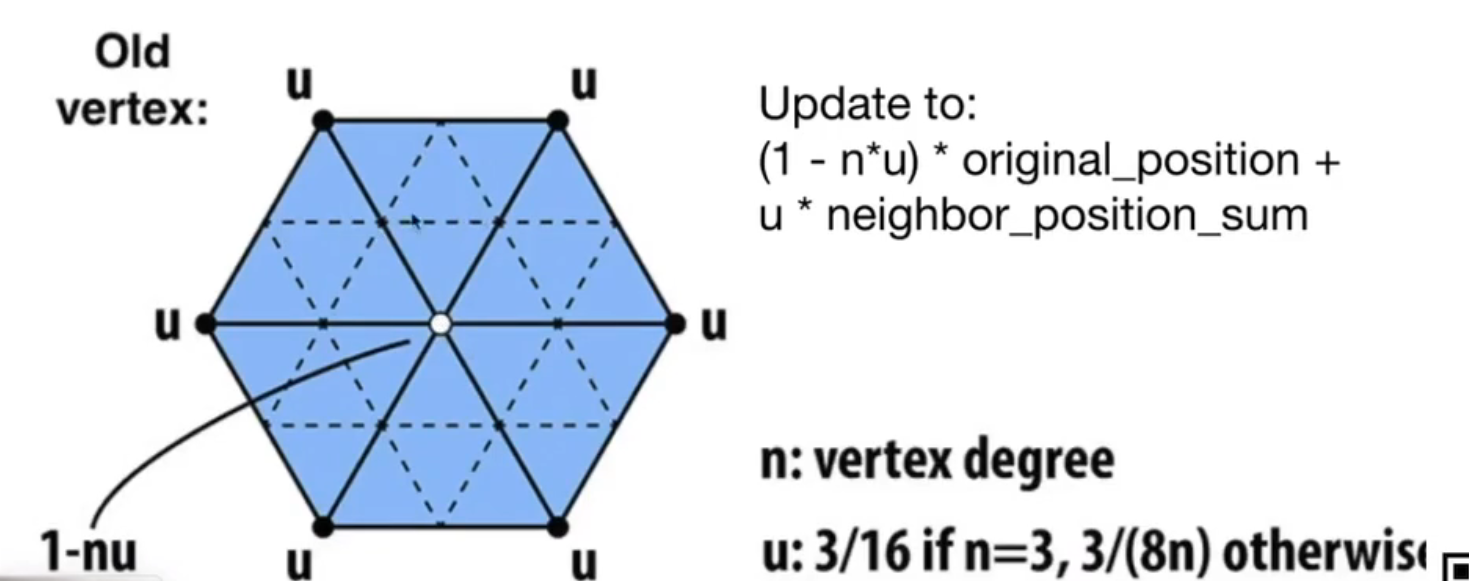
也就是说,老节点的更新,不仅取决于周围的点(权重 \(u * n\)),也取决于自己本身(权重 \(1-u*n\))。这就是卷积的思想。
另外,如果 \(n=3\),周围的权重会更高一些(i.e. \(\frac 9 {16}\));如果 \(n > 3\),就是 \(\frac 3 8\)。
Catmull-Clark Subdivision¶
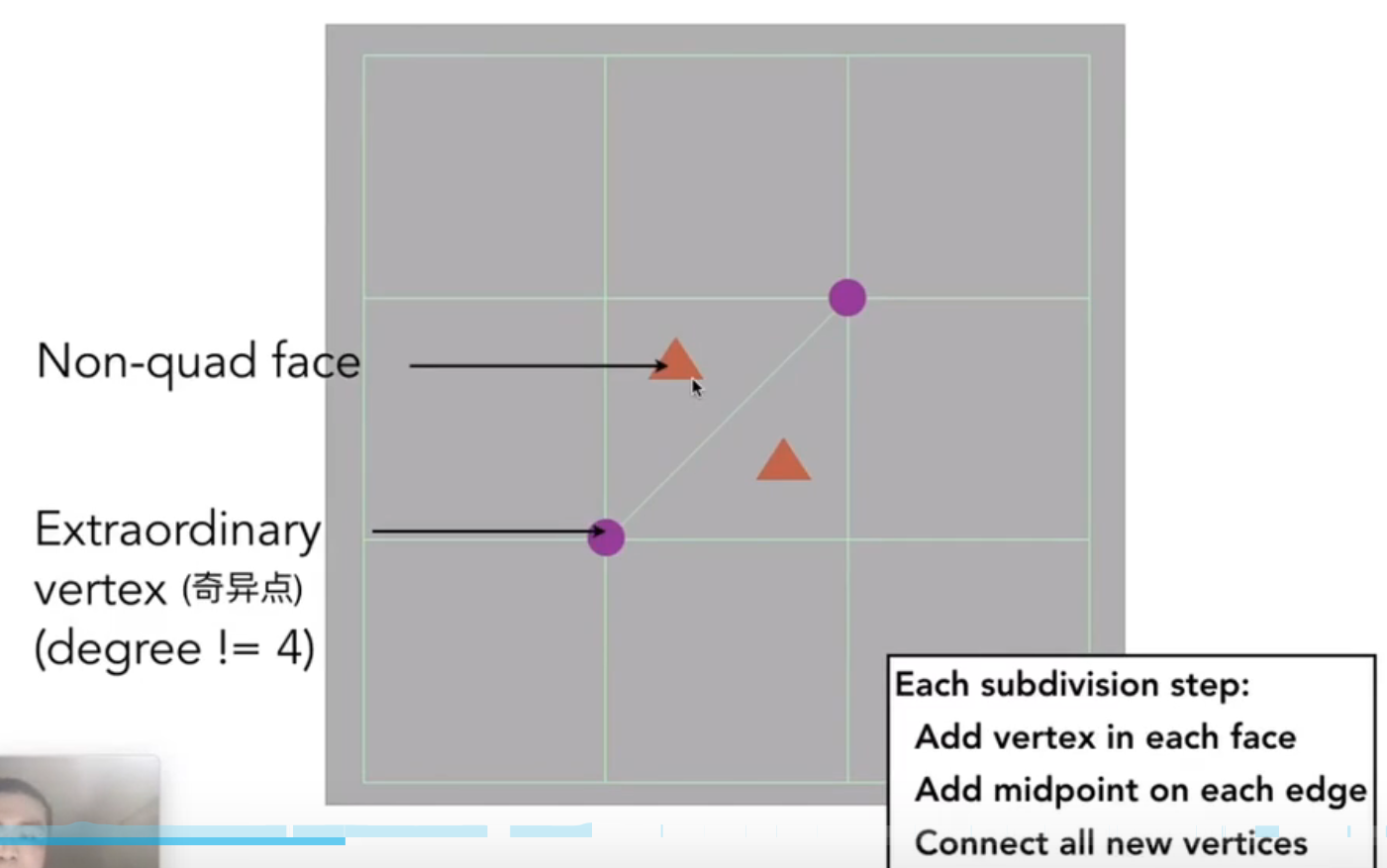
性质:
- 每次更新,旧的点的 degree 不会改变
- 也就是,旧的奇异点,仍然是奇异点
- 每次更新,在每个面上取一个点,每条边上取一个点。连接面上的点和该面对应的边上的点。
- 对于非四边形面(中间取的点),在一次细分之后,都会变成奇异点
- 对于边上新增的点,假设该边非边缘(i.e. shared by two shapes),则必然会度为 4,从而不是奇异点
- 但是,再继续做下去,由于之后的非四边形都变成了四边形,所以奇异点的数量不再增加。如下图所示:
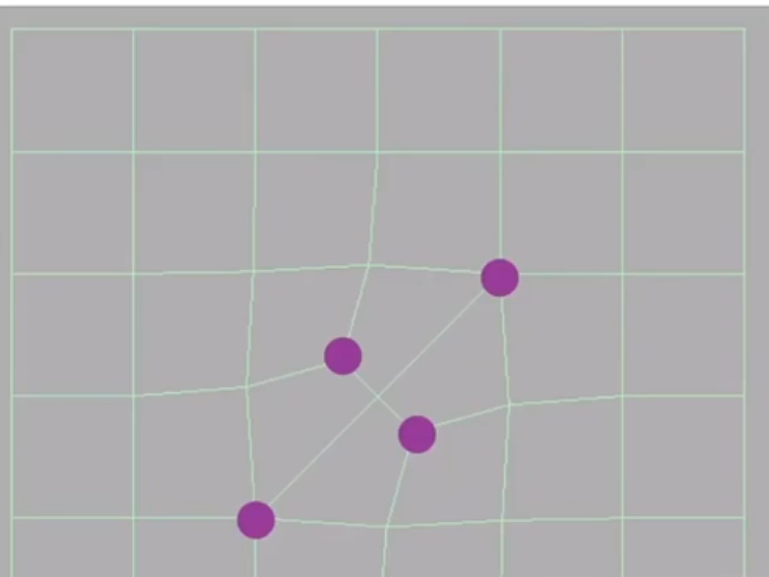
- 更新规则:
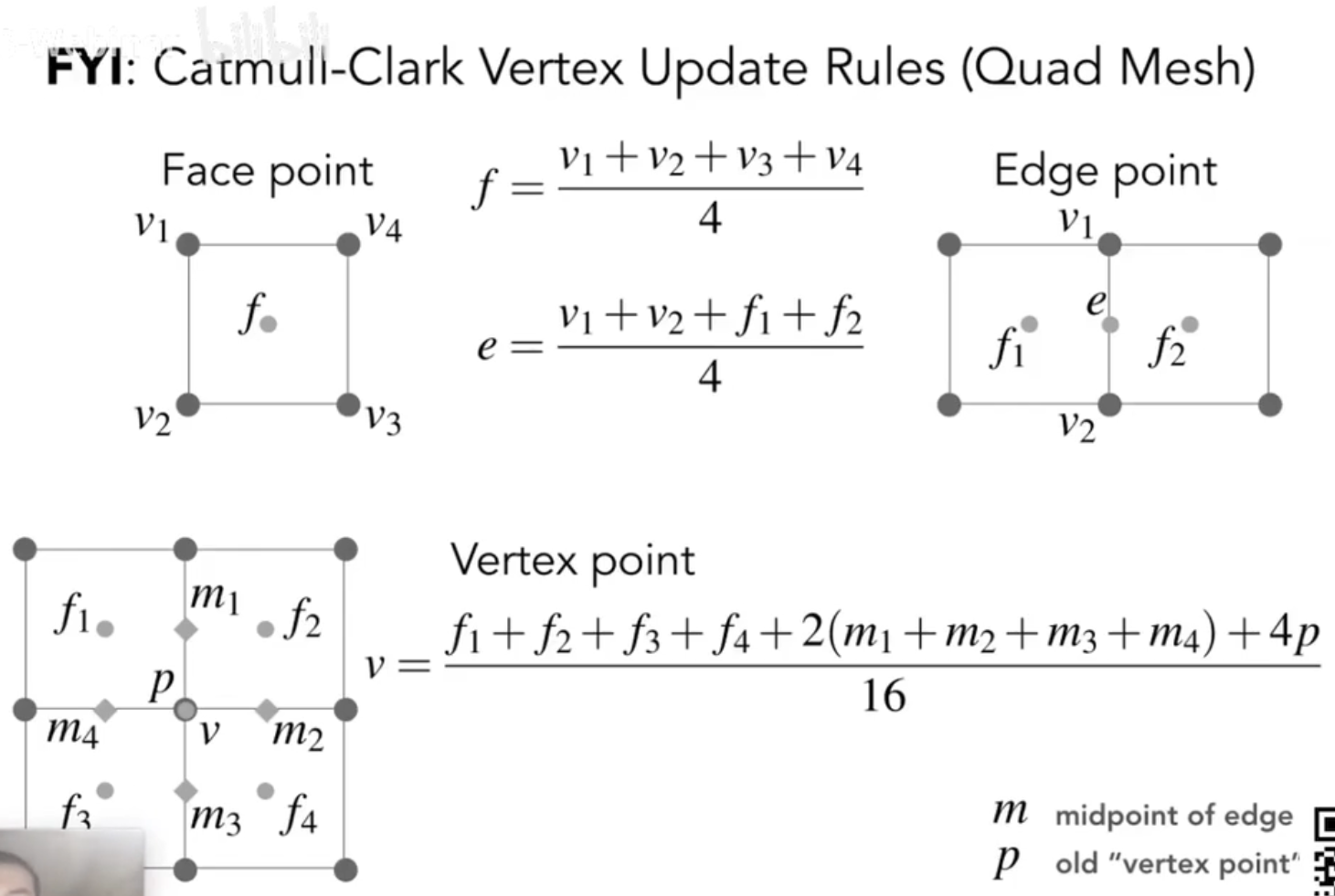
Mesh Simplification: downsampling¶
如果现在有一个网格,在远处无法看清细节,那么就可以用三角形数量较少的模型进行渲染(也就是降低分辨率),但是仍然维持原 meshes 之间的连接关系。此谓 downsampling。
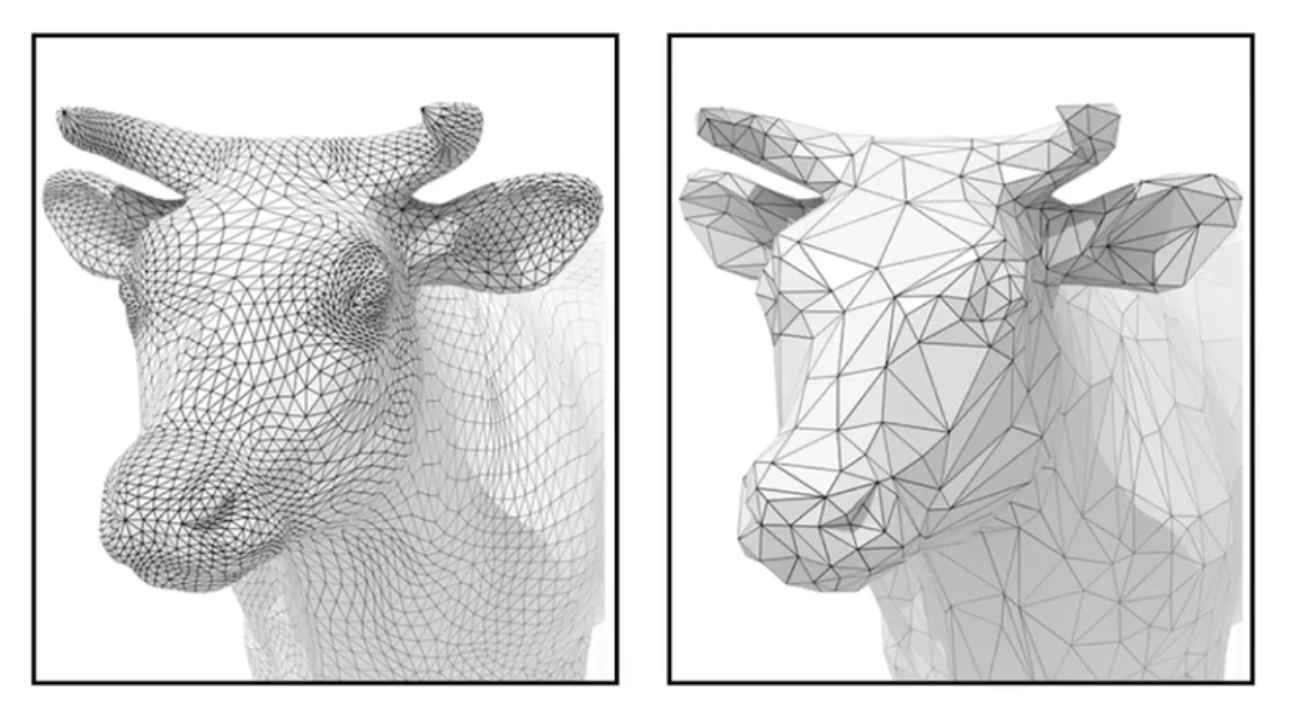
如何简化?我们肯定不能用删除三角形这种简单粗暴的方法进行简化。我们可以使用 Edge Collapsing 的方式对边进行简化。
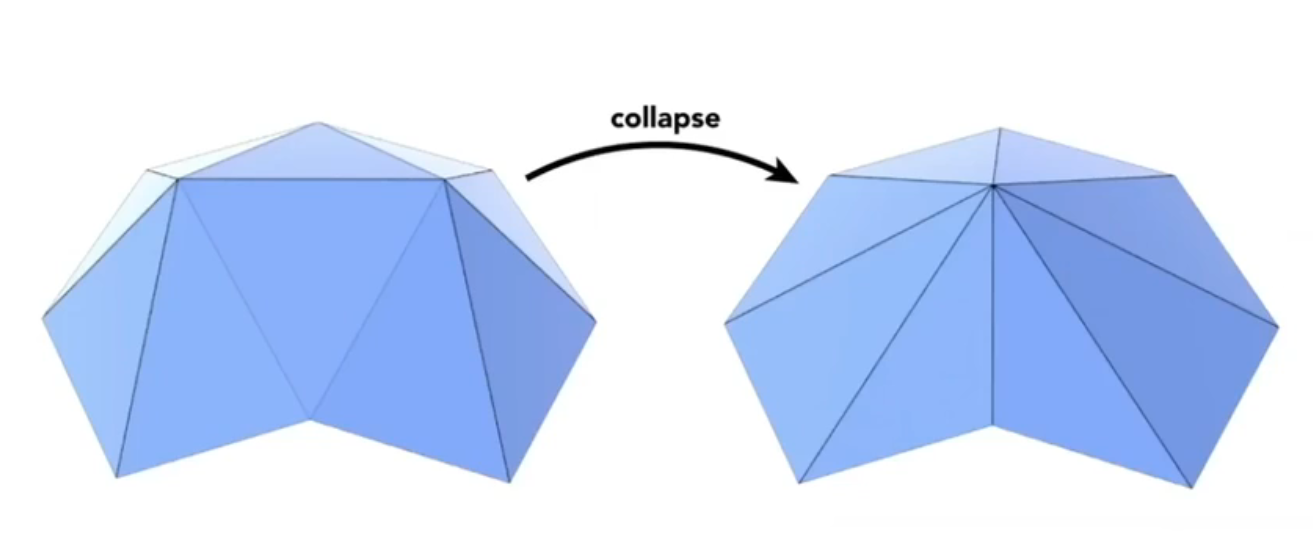
具体对哪一条边进行简化?应该建立一种 loss 的衡量方式,并选出 loss 最小的边。我们这里就采用 Quadratic Error Metrics
Quadratic Error Metrics¶
首先,假设仿射平面为 \(ax+by+cz+d = 0, \text{s.t. }a^2 + b^2 + c^2 = 1\),那么,对于任何一个点 \({\mathbf v} = \begin{pmatrix} x & y & z & 1 \\\end{pmatrix}^\intercal\),令
- \(\mathbf p= \begin{pmatrix} a & b & c & d \\ \end{pmatrix}^\intercal\)
- \(Q_{\mathbf p} = {\mathbf p}{\mathbf p}^\intercal = \begin{pmatrix} a^2 & ab & ac & ad \\ ab & b^2 & bc & bd \\ ac & bc & c^2 & cd \\ ad & bd & cd & d^2 \\ \end{pmatrix}\)
\(v\) 到平面的距离平方就为
也就是一个二次型。
其次,我们希望将每个点 \({\mathbf v}\) 都赋予一个 \(Q_{\mathbf v}\),该 \(Q_{\mathbf v}\) 就是该点相邻所有平面的 \(Q_{\mathbf p}\) 之和,即:\(Q_{\mathbf v} = \sum_{\mathbf p \in \operatorname{plane}({\mathbf v})} Q_{\mathbf p}\)。
从而,合并一个点对 \(({\mathbf v}_1,{\mathbf v}_2)\) 的时候,loss 就是:
利用最优化,我们找到这样的 $\bar {\mathbf v}^* = \arg \min \text{loss}_{\bar {\mathbf v}} $,并令 \(({\mathbf v}_1,{\mathbf v}_2)\) 的 loss 为 \(\text{loss}_{\bar{\mathbf v}}\)。
当然,这个最优化也很简单,利用简单的求偏导:
$$ \overline{\mathbf v} = \begin{bmatrix} q_{11} & q_{12} & q_{13} & q_{14} \ q_{21} & q_{22} & q_{23} & q_{24} \ q_{31} & q_{32} & q_{33} & q_{34} \ 0 & 0 & 0 & 1 \ \end{bmatrix}^{-1}
\begin{bmatrix} 0 \ 0 \ 0 \ 1 \end{bmatrix} $$
一般而言,矩阵是可逆的。如果矩阵不可逆,那么就再加一个约束:\(\bar{\mathbf v} = \operatorname{span}(\mathbf v_1 , \mathbf v_2)\)。
如果仍然多解,那就分别计算两点以及中点,三者取其小。
最后,就是算法步骤:
- 建立一个小根堆
- 将所有 valid vertices pairs 的对应 loss 求出来
- 通常,所有边都是 valid vertices pair
- 给定 \(t\),所有 \(\mathrm d({\mathbf v}_1,{\mathbf v}_2) < t\) 的点对都是 valid vertices pair
- \(t=0\) 时,只有边是 valid
- \(t\) 一般不能太大,否则所有点对都计入了,时间复杂度变成 \(\mathcal O(n^2)\) 了,太大了
- 删除堆顶
- 在逻辑上,我们令 \(\mathbf v_1 = \bar{\mathbf v}\),并删除 \(\mathbf v_2\)
- 重新计算所有受影响的点(i.e. 与 \({\mathbf v}_1,{\mathbf v}_2\) 共面的点,不含 \({\mathbf v}_2\),含 \({\mathbf v}_1\))的矩阵
- 将所有含有受影响的点的点对(i.e. 存在与 \({\mathbf v}_1,{\mathbf v}_2\) 共面的点的点对,不含 \({\mathbf v}_2\),含 \({\mathbf v}_1\))取出来,并重新计算这些点对的 loss
- 注意:对于含有 \(\mathbf v_2\) 的点对,我们合并至 \(\mathbf v_1\) 中去
- 优化:可以将受影响的点打上标记,从而在含有这些点的点对上浮到堆顶的时候,我们再对其进行 recalculate
- 重复步骤 3,直至合并了足够多的点对
算法性能分析:
本质上,\((\mathbf v_1, \mathbf v_2)\) 的 loss,只跟局部的性质有关,因此实际上是某种意义上的贪心算法。这并不能保证全局最优性。当然,实际情况下,实际的结果和最优解还是接近的。
图例:
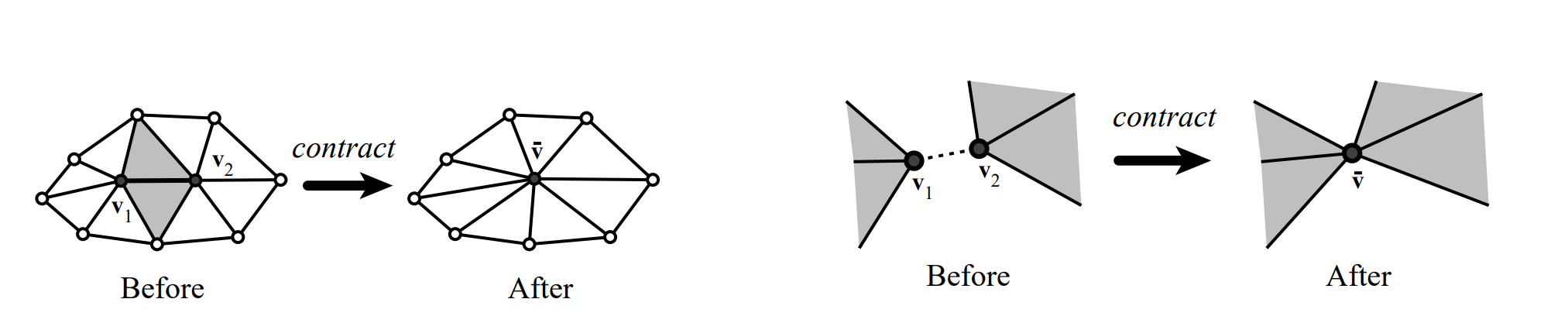
Edge contraction and non-edge contraction.

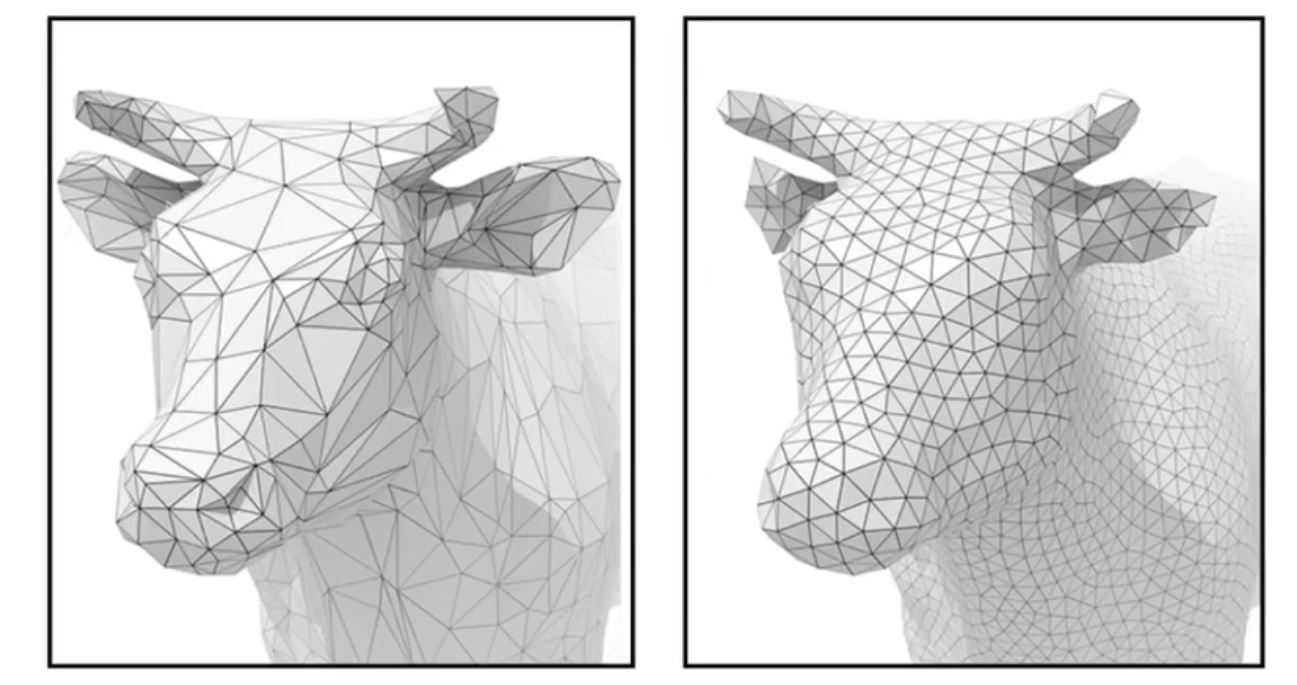
The original model on the left has 5,804 faces. The approximations to the right have 994, 532, 248, and 64 faces respectively.
Mesh Regularization¶
我们希望把奇形怪状(如细长等)的三角形,转换成近似正三角形。
Shadow Mapping¶
我们希望生成逼真的阴影,因此可以使用 Shadow Mapping(阴影映射)。
基本步骤:
- Render From Light
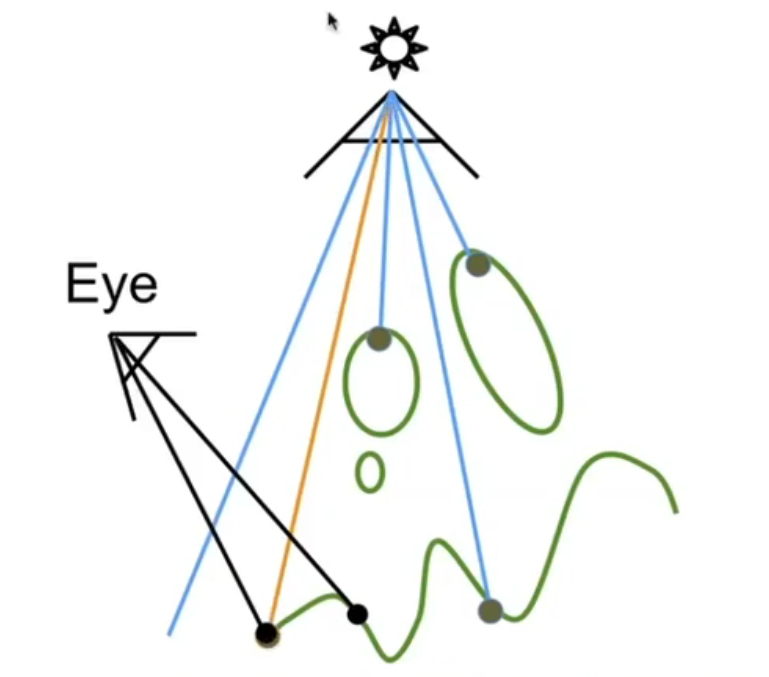
从光源看向场景,记录看到的所有点的最大深度(如图中白圈所示)。
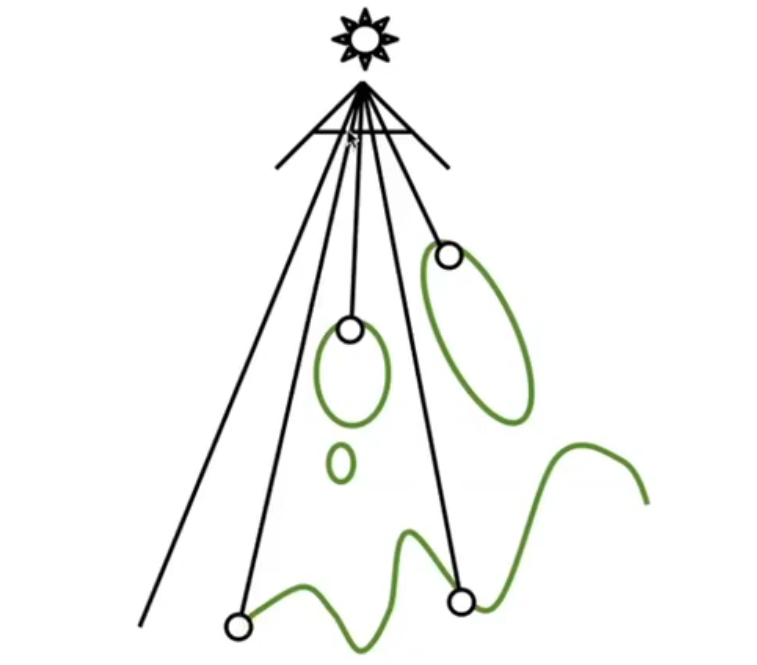
-
Render From Eye 从眼睛处看向场景
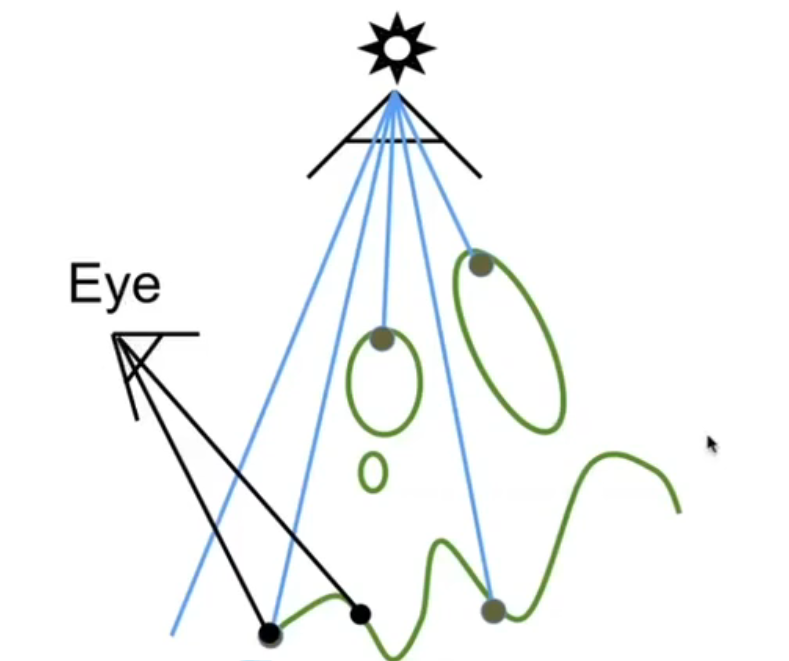
-
Project To Light 把眼睛看到的点投影回光源,从而知道该点记录在光源的深度图的哪一个像素处
如果深度等于深度图,则光线可以照到;如果深度大于深度图,则无法照到。
- 如下图所示,左点可以照到,右点不可以
主要问题:
-
硬阴影(Hard Shadows):严格按照基本方法的话,只能渲染点光源,而不能渲染有一定大小的光源。
-
名词解释:前者产生的阴影的边缘很“硬”,所以称为硬阴影;后者产生的阴影的边缘是渐变的,所以称为软阴影
-
浮点误差:光源的深度图和 "Project To Light" 一步得出的深度的浮点误差是难以抹去的。 所以,我们可以想到使用以下的策略
-
如果 "Project To Light" 算出的深度小于光源的深度图,那么也算有光
- 只要深度之差在 bias 以内,都算有光
但是,这些方法,其实实际效果并不理想
- 走样问题:如果屏幕分辨率高,但是投影的 shadow map 的分辨率低(i.e. 光源看向场景的 map 的分辨率低),那么阴影就会带有锯齿,从而很难看 如果用更高分辨率的 shadow map,则计算开销就会很大