Lec 4: Floating Points¶
Before 1985, there wasn't a universal representation of floating point numbers. So one program working on one machine might not be working on another.
IEEE Standard 754¶
The IEEE 754 Floating Point Representation is shown below:
1 bit 8 bits 23 bits
+--------------+------------------+-----------------------+
| Sign | Exponent | Mantissa |
+--------------+------------------+-----------------------+
Here, the number represented is $$ (-1)^{S}M2^{E} $$ where normally, \(M \in [1.0, 2.0)\).
And, in the representation
- \(S\) = sign field
- exp field encodes E (but is not equal to E)
- frac field encodes M (but is not equal to M)
Precise Implementation for IEEE 754¶
| Form | \(Exponent\) | \(Mantissa\) | Value |
|---|---|---|---|
| Zero | \(0\) | \(0\) | \(0\) |
| Denormalized Form | \(0\) | non-\(0\) | \((-1)^{Sgn}2^{-126}(0.Man)\) |
| Normalized Form | \(1\sim254\) | arbitrary | \((-1)^{Sgn}2^{Exp - 127}(1.Man)\) |
| Infinity | \(255\) | \(0\) | \(\infty\) |
| NaN | \(255\) | non-\(0\) | NaN |
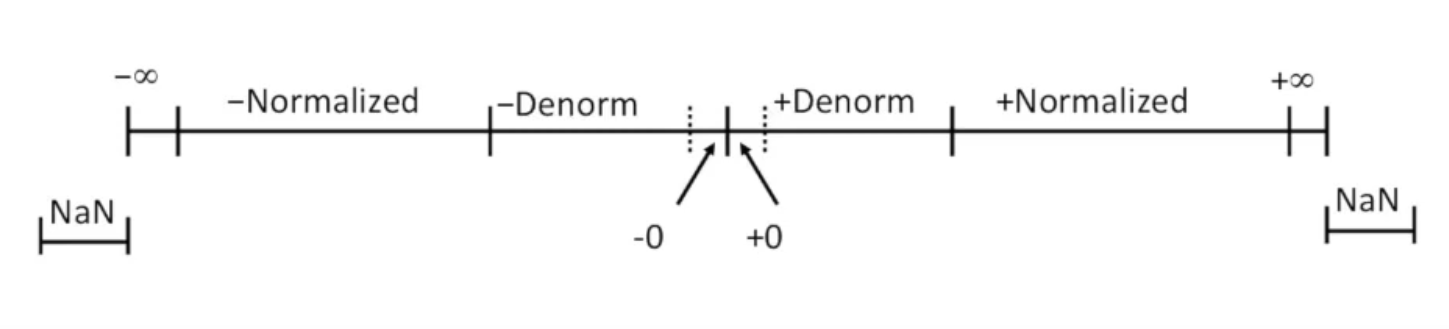
Visualization:
Some Variations of IEEE 754¶
- Single Precision: (1, 8, 23) ------------------------------> 32 bits
- Double Precision: (1, 11, 52) --------------------------> 64 bits
- Extended Precision (Intel only) : (1, 15, 63/64) --> 79/80 bits
... and also a generic definition of the forms¶
| Form | \(Exponent\) | \(Mantissa\) | Value |
|---|---|---|---|
| Zero | \(0\) | \(0\) | \(0\) |
| Denormalized Form | \(0\) | non-\(0\) | \((-1)^{Sgn}2^{1-Bias}(0.Man)\) |
| Normalized Form | \(1\sim 2^{\#E}-2\) | arbitrary | \((-1)^{Sgn}2^{Exp - Bias}(1.Man)\) |
| Infinity | \(2^{\#E}-1\) | \(0\) | \(\infty\) |
| NaN | \(2^{\#E}-1\) | non-\(0\) | NaN |
where usually \(Bias = 2^{\#E-1} - 1\).
- In the case of IEEE 754, \(Bias = 2^{8 - 1} - 1 = 128 - 1 = 127\).
Distribution of Floating Point Numbers¶
Take (1,3,2) as example.

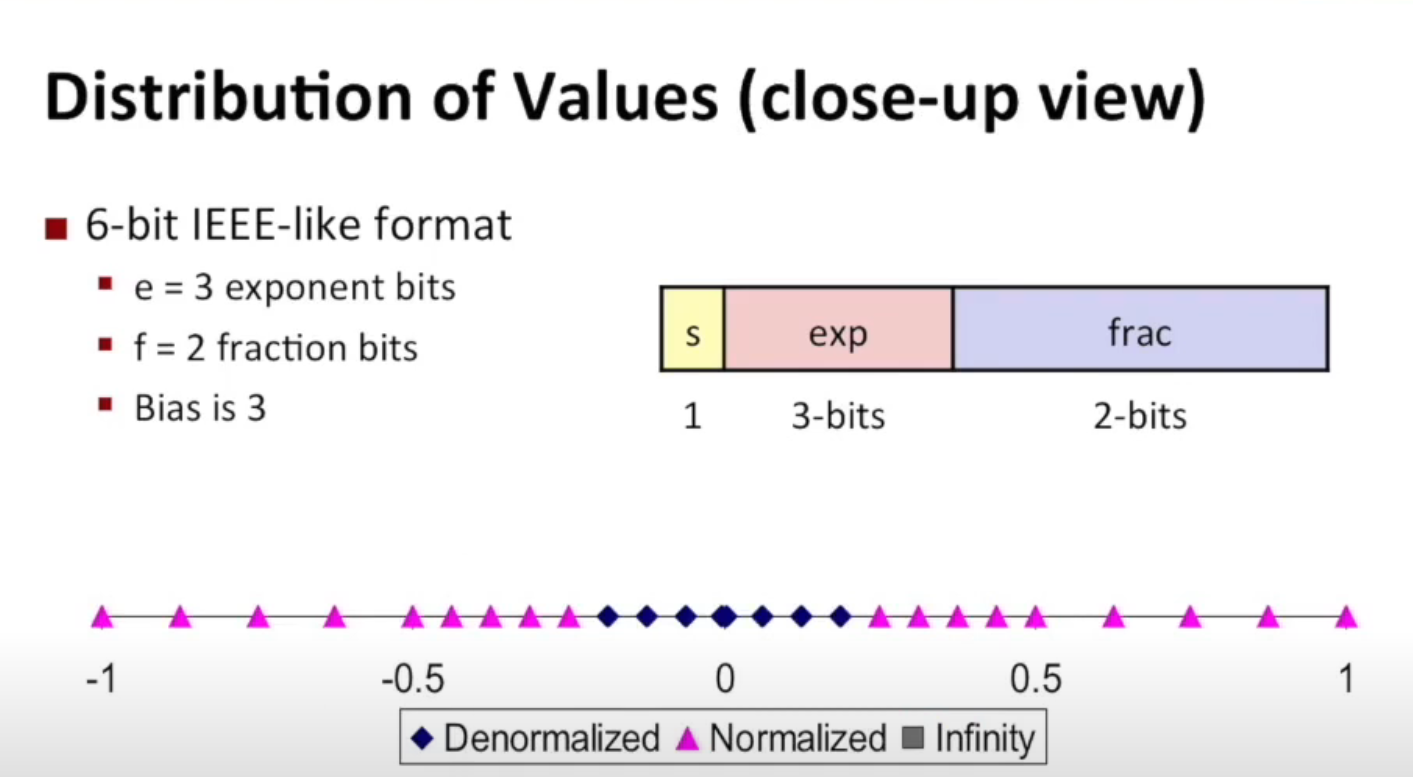
One can observe the presence of uniformly distributed values close to zero. Additionally, a step-like pattern of uniformly distributed values is apparent when examining normalized values.
Properties of the IEEE encoding¶
- FP Zero is the same as Integer Zero
- i.e. All bits = 0
- Can (Almost) Use Unsigned Integer Comparison
- Must first compare sign bits
- Must consider -0 =0
- NaNs problematic
- Will be greater than any other values
- What should comparison yield?
- Otherwise OK
- e.g. Denorm vs.normalized Normalized vs.infinity
Operations on FP¶
Basic Idea¶
First, compute the exact result.
- Assuming you have infinite amount of bits available
Next,
- make it infinity if it's too large.
- round it if it's too long
Rounding¶
There are four major ways of rounding.
| Value | Towards zero | Round down (\(-\infty\)) | Round up (\(+\infty\)) | Nearest Even (default) |
|---|---|---|---|---|
| $1.40 | $1 | $1 | $2 | $1 |
| $1.60 | $1 | $1 | $2 | $2 |
| $1.50 | $1 | $1 | $2 | $2 |
| $2.50 | $2 | $2 | $3 | $2 |
| $-1.50 | -$1 | -$2 | -$1 | -$2 |
"Nearest Even" is used in IEEE standard. But you can choose the way you round in assembly code.
How To Round?¶
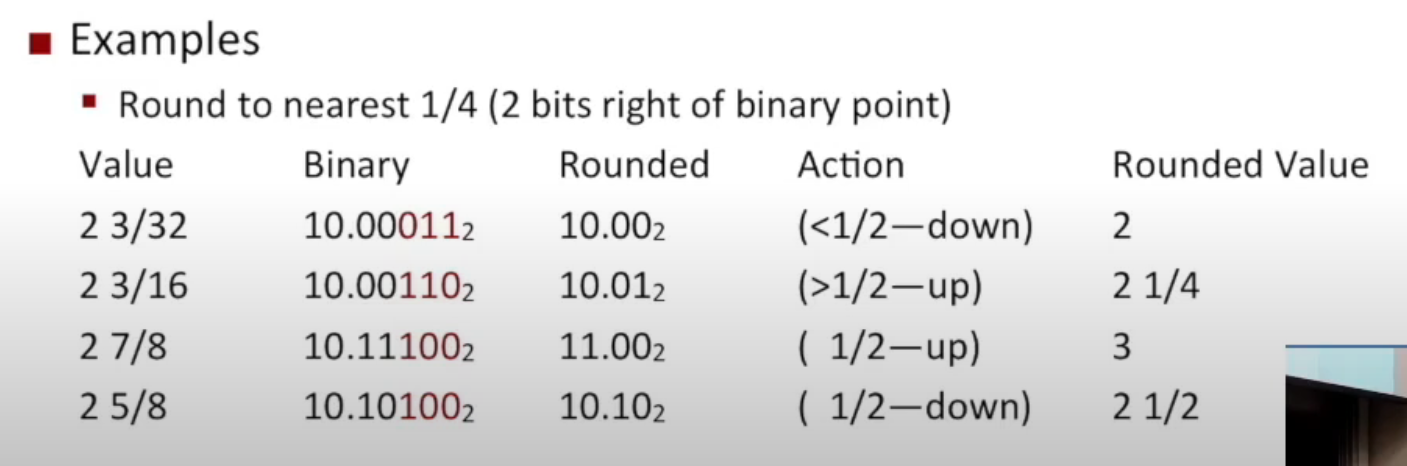
If the digits to be truncated is
- greater than 1/2: Round UP!
- smaller than 1/2: Round DOWN!
- equal to 1/2: Round EVEN!
ROUND_TO_EVEN (x_x0.x1_x2_..._xn)
IF (x1 & (!x2_..._xn)) BEGIN
x_x0 := x_x0 + x1
END ELSE BEGIN
// x1_x2_..._xn == 10...0
x_x0 := x_x0 + x0;
END
ENDFUNCTION
Multiplication¶
-
$ (-1)^{s_1} M_1 2^{E_1} \times (-1)^{s_2} M_2 2^{E_2} $
-
Exact Result: $ (-1)^s M 2^E $
-
Sign
s: \(s_1 \oplus s_2\) -
Significand
M: \(M_1 \times M_2\) -
Exponent
E: \(E_1 + E_2\) -
Fixing
-
If \(M \geq 2\), shift
Mright, incrementE- note that both \(M_1, M_2 \in [1.0, 2.0)\), so their product must be smaller than \(4.0\).
-
If
Eis out of range, overflow -
Round
Mto fit fractional precision -
Implementation
- The biggest chore is multiplying significands.
Addition¶

Mathematical Properties of FP Add and Mul¶


Tip:
- In nature, things change smoothly. So you seldom run into the problem of non-associativity.
- But in some fields, e.g financial market, the indices vary dramatically. So you might run into problem, if you use default FP representation.
FP in C¶
C guarantees two levels
float: "single precision"double: "double precision"
Casting (between int, float, and double)
int\(\to\)double: No rounding neededint\(\to\)float: Asfloatonly has mantissa of 23 bits, it might round according to a certain rule.float/double- truncate fractional part
- i.e. round to zero
- not defined when out of range or NaN, but usually to
TMin(i.e. \(-2147483648\))