Skip to content

Lec 12: Cache Memories

Introduction

  • Cache memories are small, fast SRAM-based memories managed automatically in hardware
  • Hold frequently accessed blocks of main memory
    • Note that data is copied in block-sized transfer units
  • CPU looks first for data in cache memory

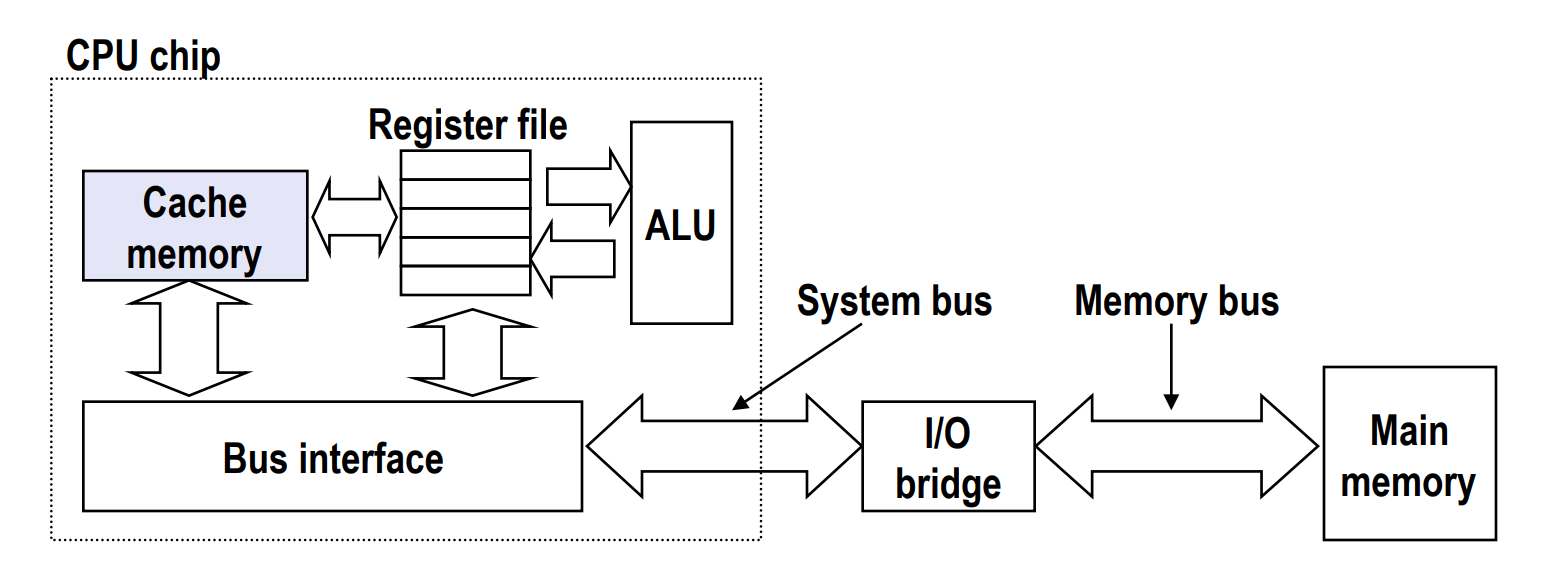
image-20240124164904138

General Cache Organization

First of all, cache memories are completely managed by hardware. So the hardware must be able to look up for a block in cache, meaning the cache memories have to be strictly yet simply organized.

image-20240124165304317

As shown in the picture, the cache memory contains \(S=2^s\) sets. Each set contains \(E = 2^e\) lines.

There are

  • a valid bit
  • indicating whether the block is valid or not, since they are random bits when initialized
  • a tag
  • a block that contains \(B=2^b\) bytes

Finally, we consider the total size of blocks to be the size of the cache, i.e. cache size \(C = S * E * B\).

Cache Operations

Cache Read

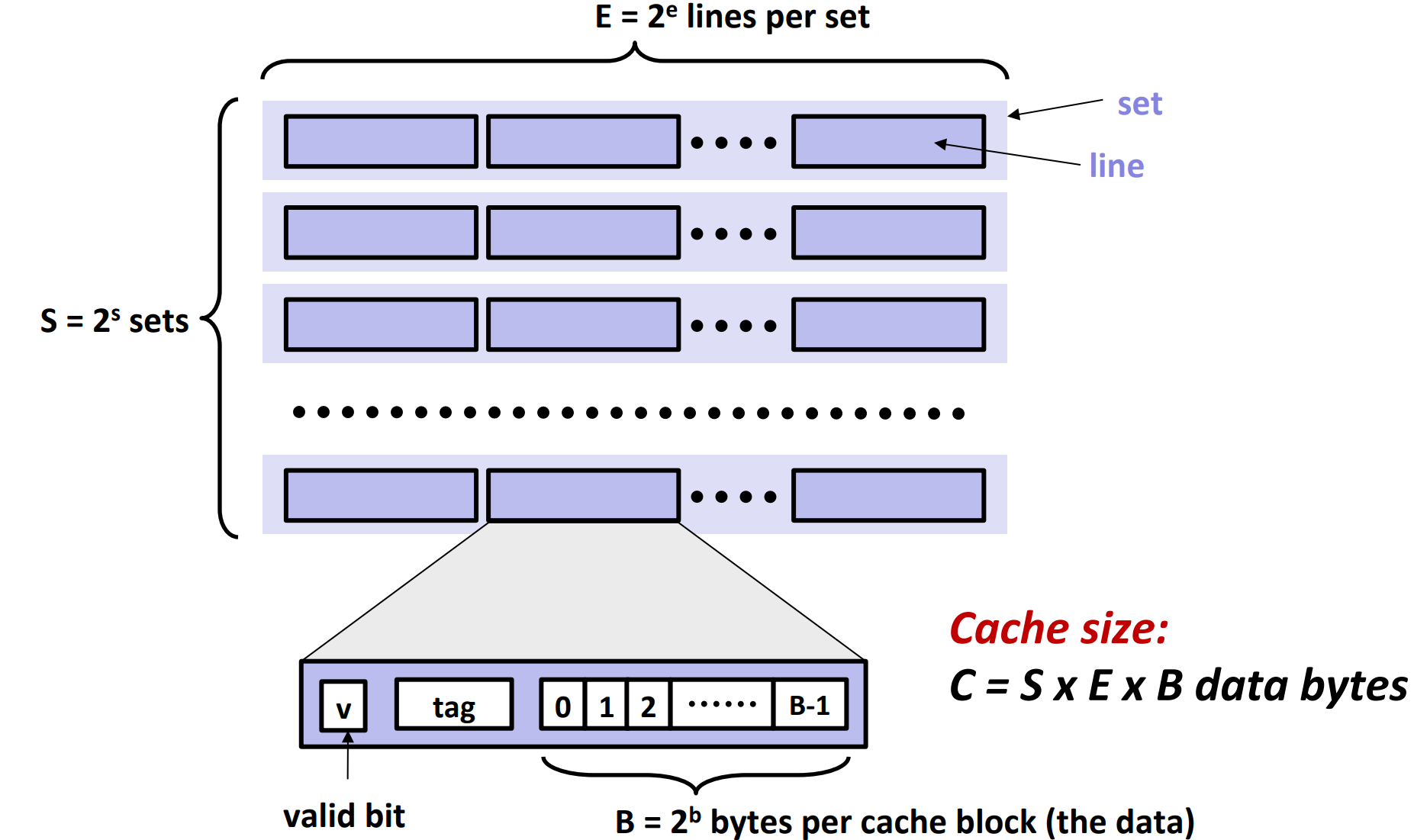
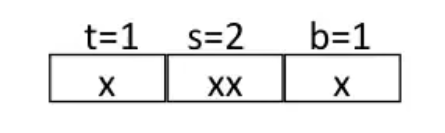
We divide the address of a word in three parts: tag, set index and block offset.

Steps:

  1. Go to the corresponding set
  2. Check line by line whether there is a line whose
  3. valid bit is 1
  4. and tag equals to the tag of the word
  5. If there is, we use the b bits to determine where the data is in that block

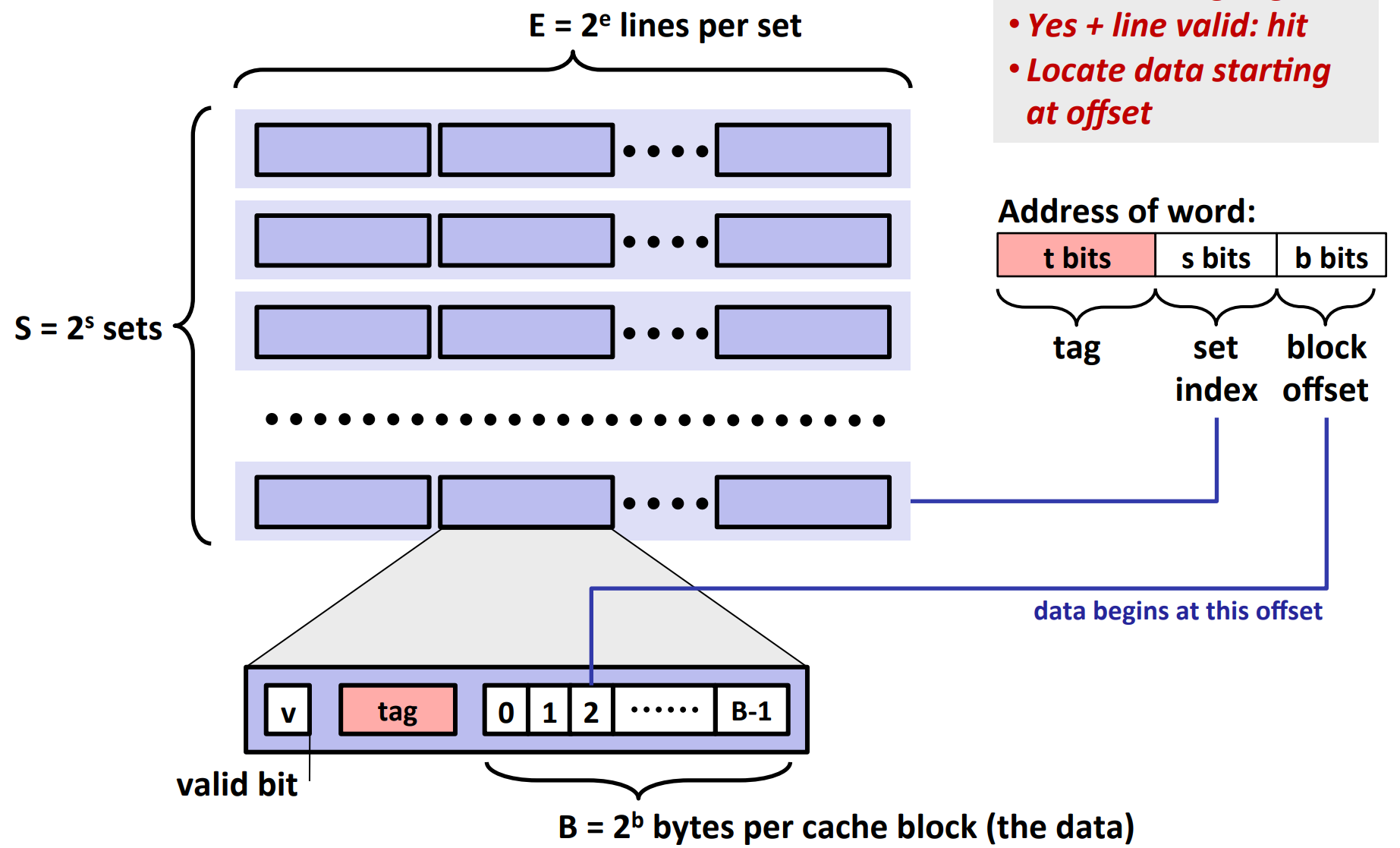
image-20240124170523219

Disadvantages of Direct-Mapped Cache Simulation

Definition of direct-mapped cache: cache where \(e = 0\) and thus \(E = 1\)

Suppose we have a cache memory where

  • memory size \(M=16\) bytes(4-bit addresses)
  • \(B=2\) bytes/block
  • \(S=4\) sets
  • \(E=1\) Blocks/set
  • i.e. image-20240124172648972

If we read addresses in the following order, there will be a conflict miss when reading address 0 again. And it's caused by small number of lines per set.

image-20240124172728111

E-way Set Associative Cache

Take \(E=2\) as an example:

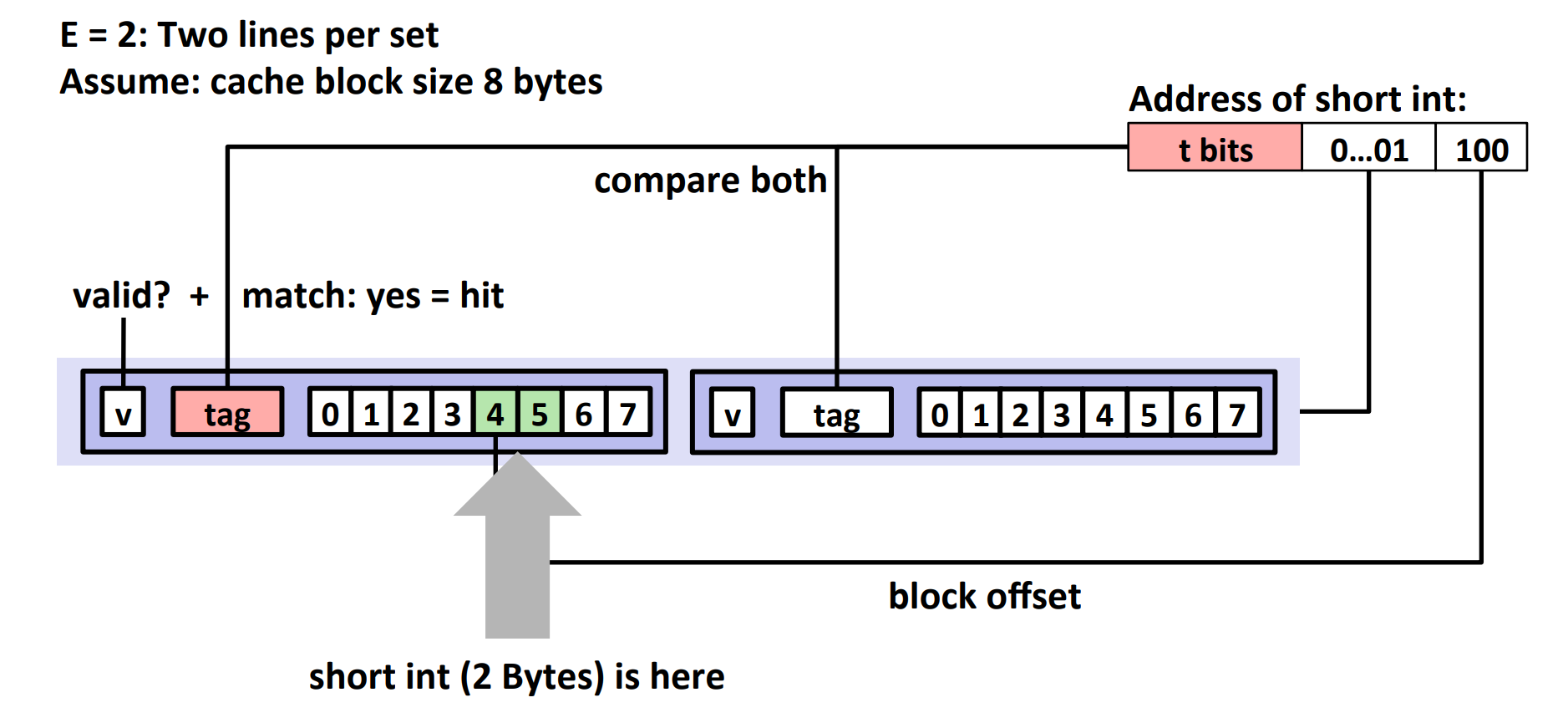
image-20240124174201697

If there is no match:

  • one line in set is selected for evection and replacement
  • replacement policies: random, least recently used (LRU), ...

Advantages of E-way Set Associative Cache

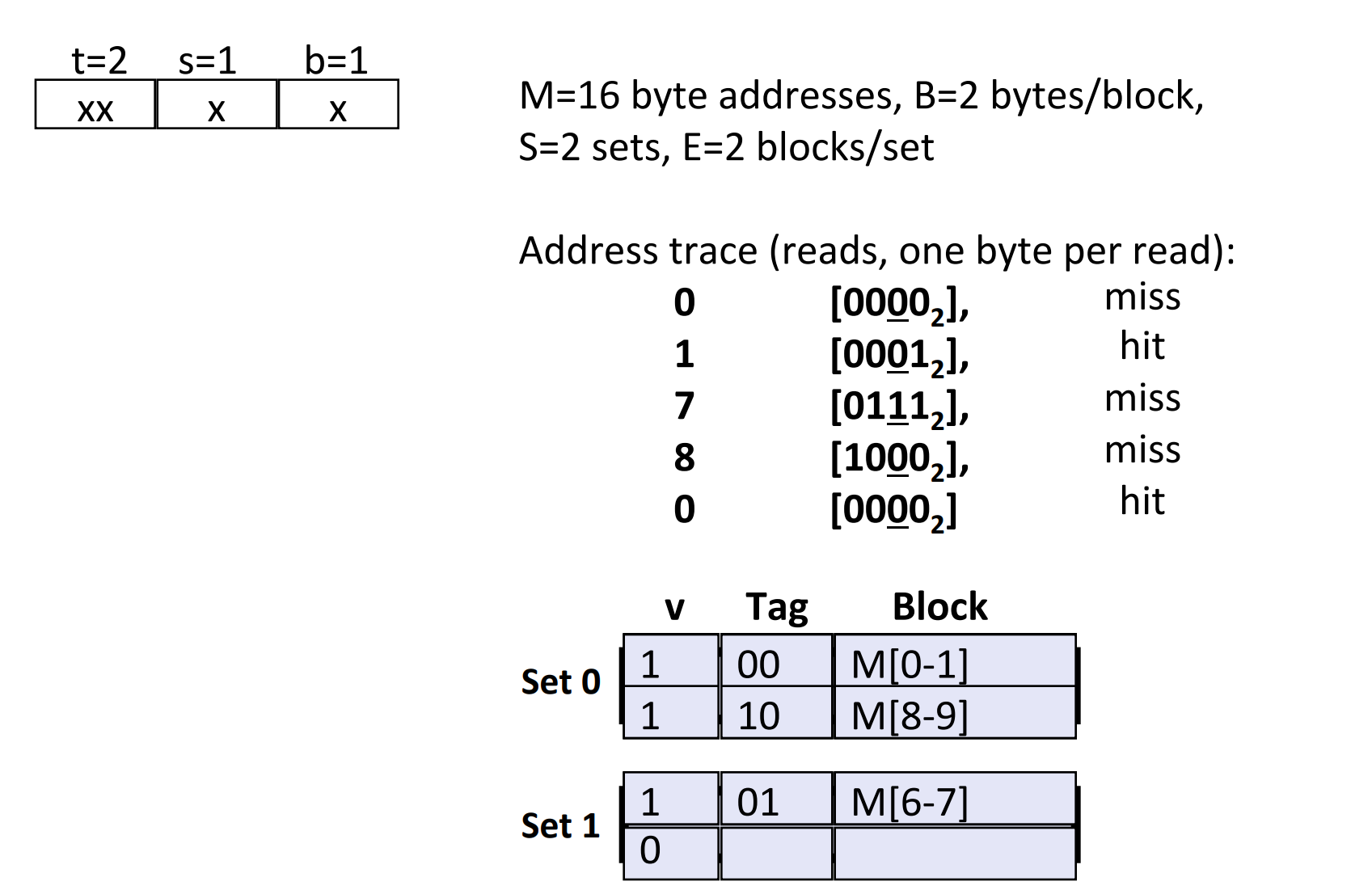
image-20240124174408866

As shown in the picture, if we read addresses in the following order, there will NOT be a conflict miss when reading address 0 again. Since the capacity of one set is not that small.

Cache Write

Write is somewhat more complicated than read, since we have multiple copies of data exist in the system:

  • L1, L2, L3, Main Memory, Disk, ...

So, there are two problems we have to consider:

  1. What to do on a write-hit?
  2. Write-through (i.e. write immediately to memory as well as cache)
  3. Write-back (i.e. defer write to memory until replacement of line)
    • and this needs a dirty bit
  4. What to do on a write-miss?
  5. Write-allocate (i.e. first load into cache, then update line in cache)
    • Good if more writes to the location follow
  6. No-write-allocate (i.e. writes straight to memory, doesn't load into cache)

Typically,

  • Write-through + No-write-allocate
  • Write-back + Write-allocate

Cache Hierarchy for Intel Core i7

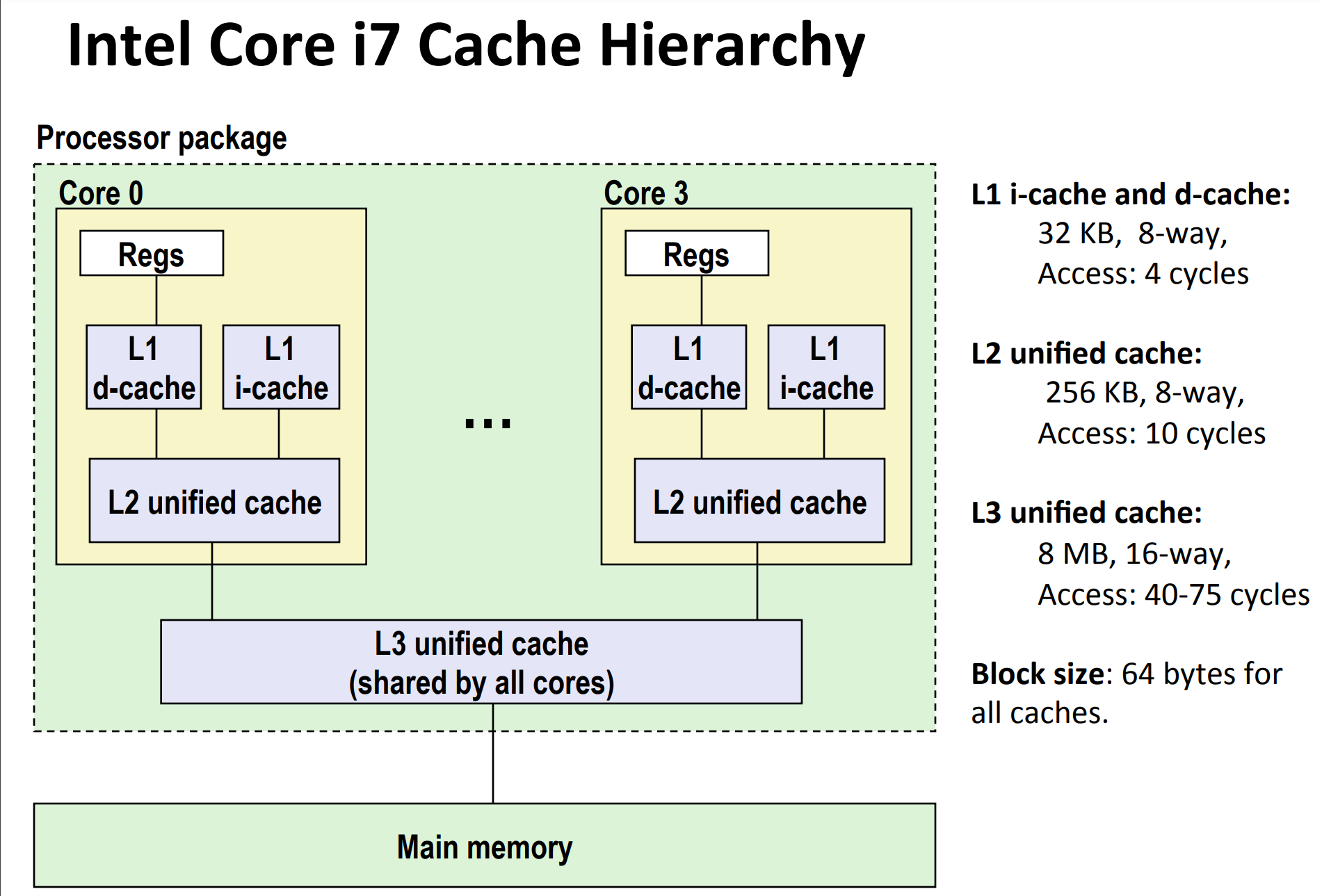
image-20240124223947853

Take Intel Core i7 as example. It's not hard to see that set size for L1, L2 and L3 are

  • L1: \(64 = 2^6\)
  • L2: \(512 = 2^9\)
  • L3: \(8192 = 2^{13}\)

respectively.

Cache Performance Metrics

Miss Rate

  • Fraction of memory references not found in cache (misses / accesses) = 1 - hit rate
  • Typical numbers (in percentages):
  • 3-10% for L1
  • Can be quite small (e.g., < 1%) for L2, depending on size, etc.

Hit Time

  • Time to deliver a line in the cache to the processor

  • Includes time to determine whether the line is in the cache

  • Typical numbers:

  • 4 clock cycles for L1
  • 10 clock cycles for L2

Miss Penalty

  • Additional time required because of a miss
  • Typically 50-200 cycles for main memory (Trend: increasing!)

Formula: \(\mathrm{Average \ Access \ Time} = \mathrm{Hit \ Time} + \mathrm{Miss \ Rate} \times \mathrm{Miss \ Penalty}\)

For instance,

  • 97% hits: 1 cycle + 0.03 * 100 cycles = 4 cycles
  • 99% hits: 1 cycle + 0.01 * 100 cycles = 2 cycles

So, a small difference in hit rate have a huge impact on AAT.

The Memory Mountain

Test function:

long data[MAXELEMS]; /* Global array to traverse */

/* test - Iterate over first "elems" elements of
 * array “data” with stride of "stride", using
 * using 4x4 loop unrolling.
 */
int test(int elems, int stride) {
    long i, sx2 = stride * 2, sx3 = stride * 3, sx4 = stride * 4;
    long acc0 = 0, acc1 = 0, acc2 = 0, acc3 = 0;
    long length = elems;
    long limit = length - sx4;

    /* Combine 4 elements at a time 
     * for the sake of parallelization
     */
    for (i = 0; i < limit; i += sx4) {
        acc0 = acc0 + data[i];
        acc1 = acc1 + data[i + stride];
        acc2 = acc2 + data[i + sx2];
        acc3 = acc3 + data[i + sx3];
    }

    /* Finish any remaining elements */
    for (; i < length; i++) {
        acc0 = acc0 + data[i];
    }

    return ((acc0 + acc1) + (acc2 + acc3));
}

image-20240124231845086

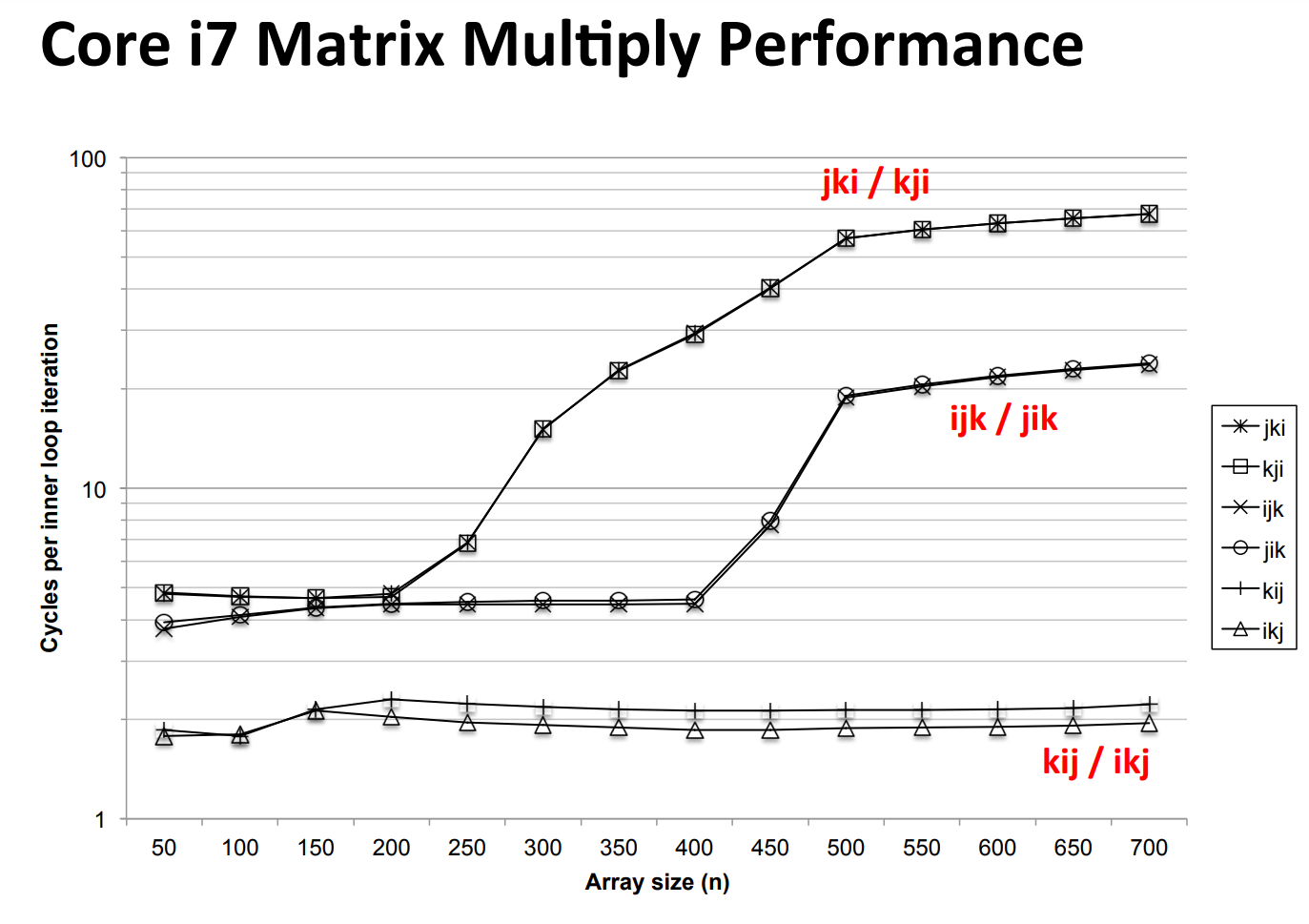
As you can see:

  • when stride = 1, the CPU seems to understand this pattern, and applies aggressive prefetching to accelerate.
  • when stride > s8, the slope tend to disappear.
  • This is because the block size is 64 bytes, and when stride > s8, there will be cache miss every time.

Optimization

Spatial Locality

image-20240125002822321

image-20240125002837725

Temporal Locality

See 矩阵分块操作 for details.

总体而言，

  • 不进行分块：\(\frac 9 8 n^3\) 次未命中
  • 进行分块（前提是 \(3B^2<C\)）：\((\frac n B)^2 2 \frac n B \frac {B^2} 8 = \frac 1 {4B} n^3\) 次未命中
  • \(\frac {B^2} 8\) 就是一个块的 cache miss。不难发现，由于块比较小，缓存可以存下所有的数据，所以不论是行优先还是列优先访问，都是一样的。 这和未优化的情况不同。 比如，未优化的情况下，列优先访问时，访问 arr[0][1] 时，arr[0][0-7] 早已从 cache 中被抹去，因此访问是 miss。 而在优化的情况下，访问 arr[0][1] 时，由于 cache 还没有满，因此 arr[0][0-7] 还在其中，访问不是 miss。
  • 因此，差异就在于，对于 \(3B^2 < C\) 的分块，一个块的数据在两个块的矩阵乘法中，不会被 cache 抹去，可以反复使用，因此可以反复使用，提高了 temporal locality 本质上，矩阵乘法只需要用到 \(\mathcal O(n^2)\) 的数据，但是却要进行 \(\mathcal O(n^3)\) 的计算，因此肯定有大量的数据复用，所以我们有 exploit 的余地。