4. Algebraic Topology
代数拓扑简介¶
简介¶
- 使用抽象代数的工具来研究拓扑空间:用代数结构具体地,定量地描述或提取拓扑空间的拓扑特征
- 与点集拓扑相比,代数拓扑具有可计算性,更易用于研究具体的拓扑空间,并能设计算法进行计算
- 代数拓扑是计算拓扑与拓扑数据分析的主要理论基础
主要分支¶
基本群¶
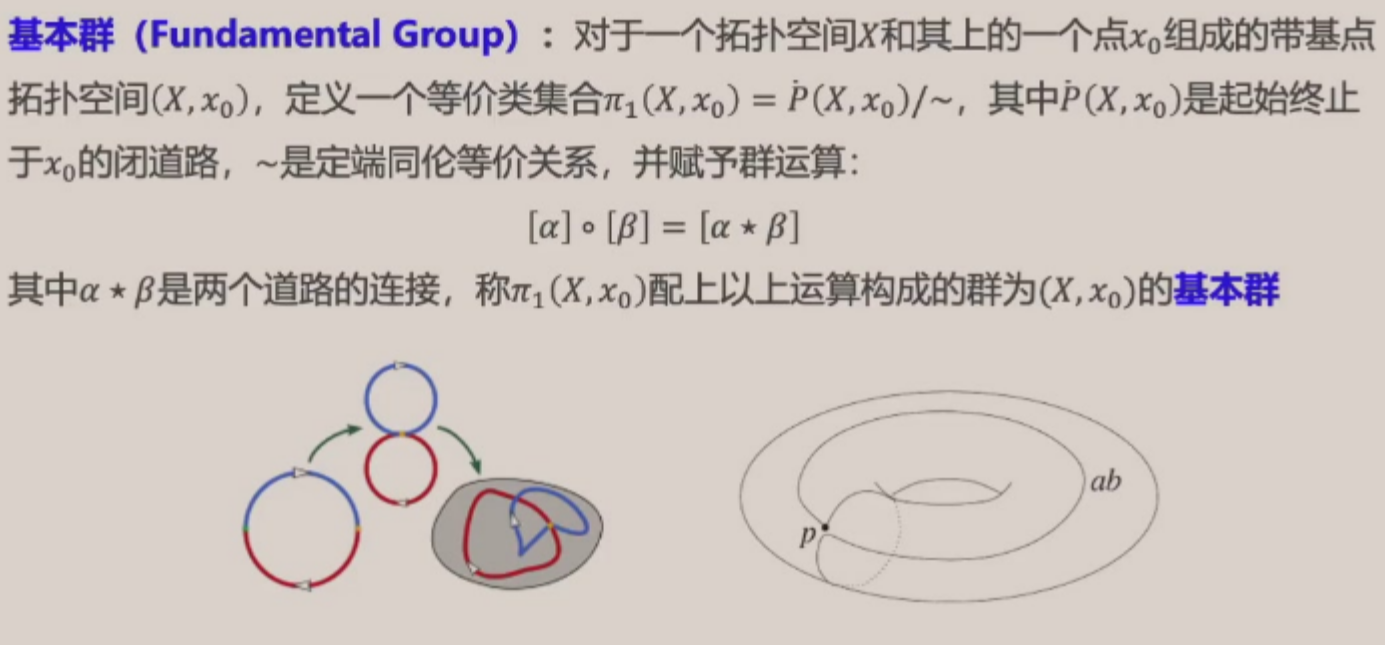
关键词:
- 闭道路:给定拓扑空间 \(X\),连续映射 \(f: \mathbb S^1 \to X\) 就是闭道路
- 高维闭道路:\(f: \mathbb S^n \to X\)
- 定端同伦:不仅同伦,而且 \(f, g\) 的两个端点相同
- 定端保证了基本群中的 \(f \star g, g \star f\) 均良定义
- 带基点的拓扑空间
- 道路连接
我们首先构造出了两个简单的(定端)同伦等价类:右图中的小圈和大圈。
然后通过群运算,得到了(也许)无穷无尽的同伦等价类。
同伦群的问题¶
如图,同伦群
- 计算复杂,即使是最简单的 \(n\) 维球面,也难以计算其高维同伦群
- 难以离散化,不利于计算机的实现
- 可能非交换,难以应用到实际的问题中
链复形与同调群¶
闭链¶
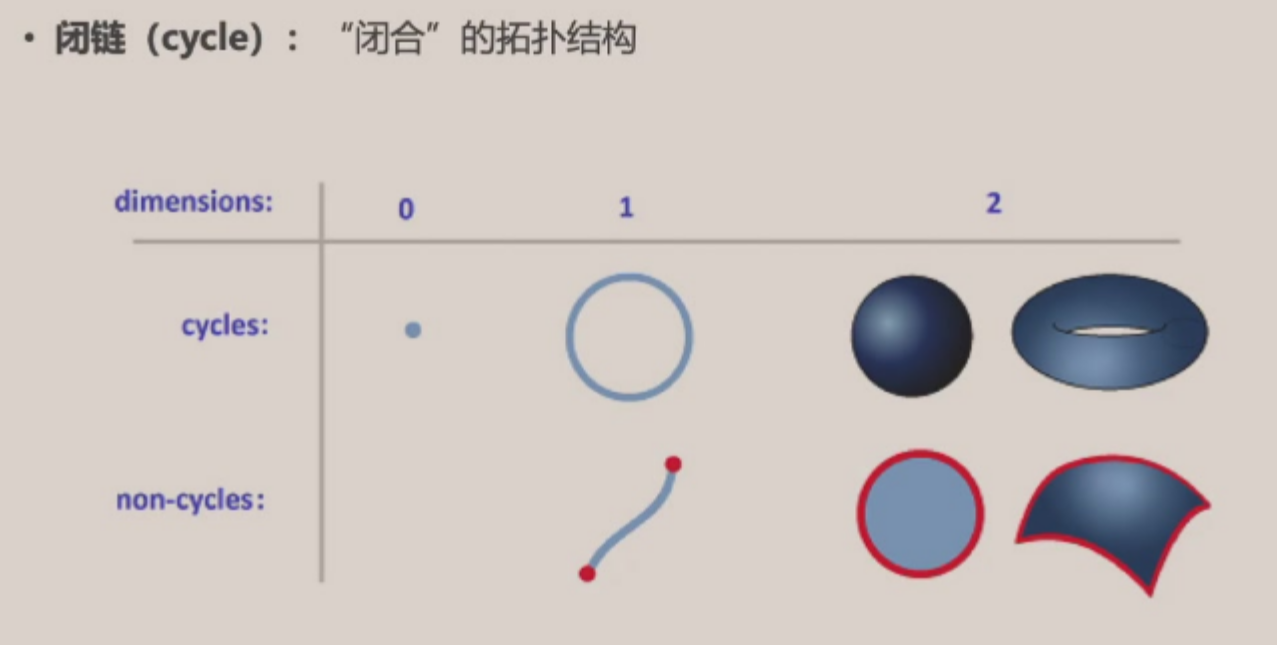
同调¶
如果两个闭链是某个拓扑子空间的所有边界,那么称这两个闭链是同调的 (homologous)。
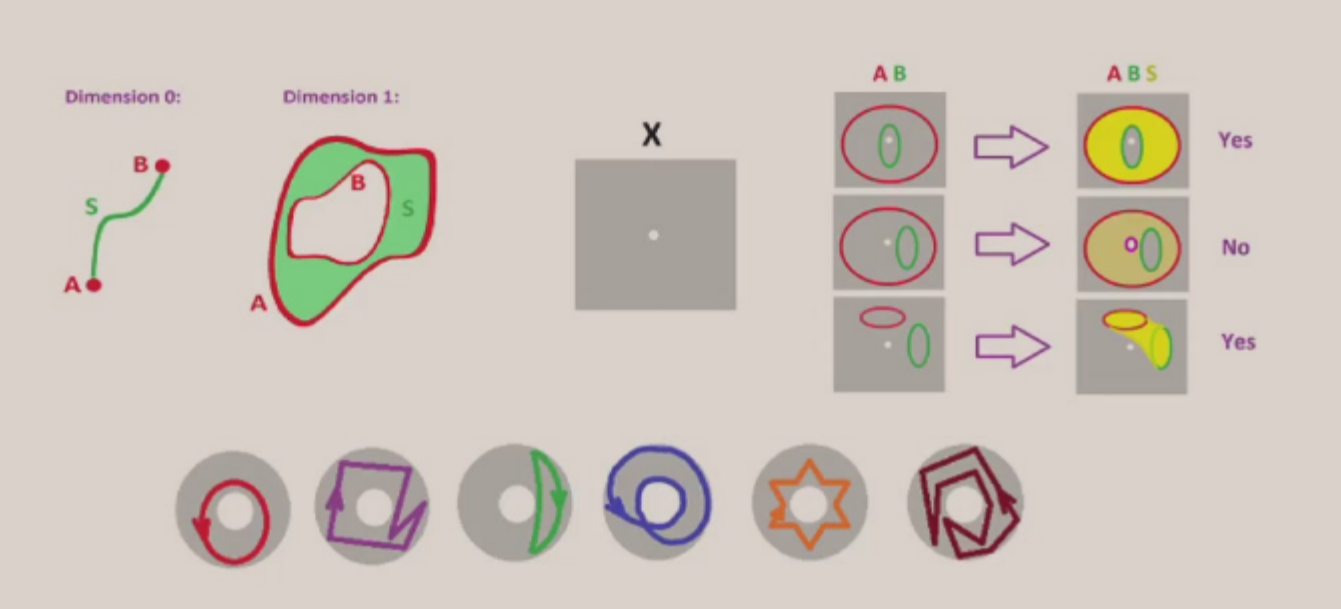
- 如上图,对于拓扑空间 \(X\),黄色部分就是一个拓扑子空间
链群¶
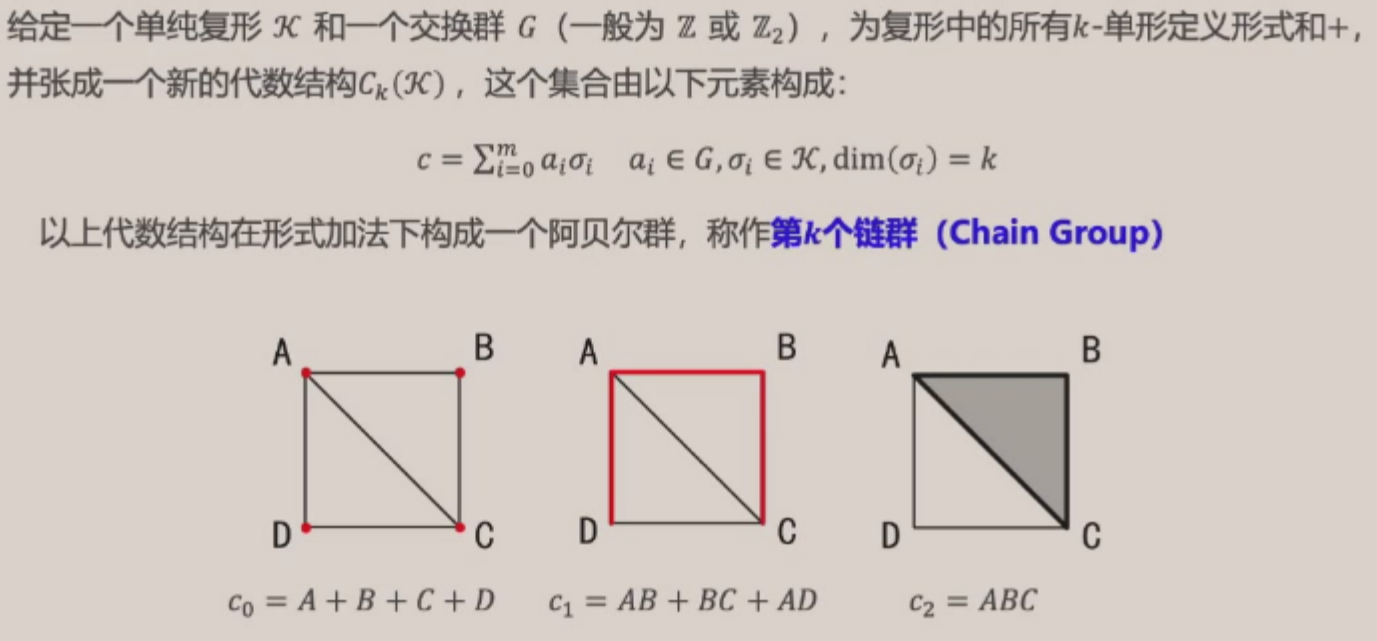
- 注意:不同维数的单形组成不同的链群
边界算子: \(\partial_k: C_k \to C_{k-1}\)¶
边界算子把不同维数的链群关联在了一起。
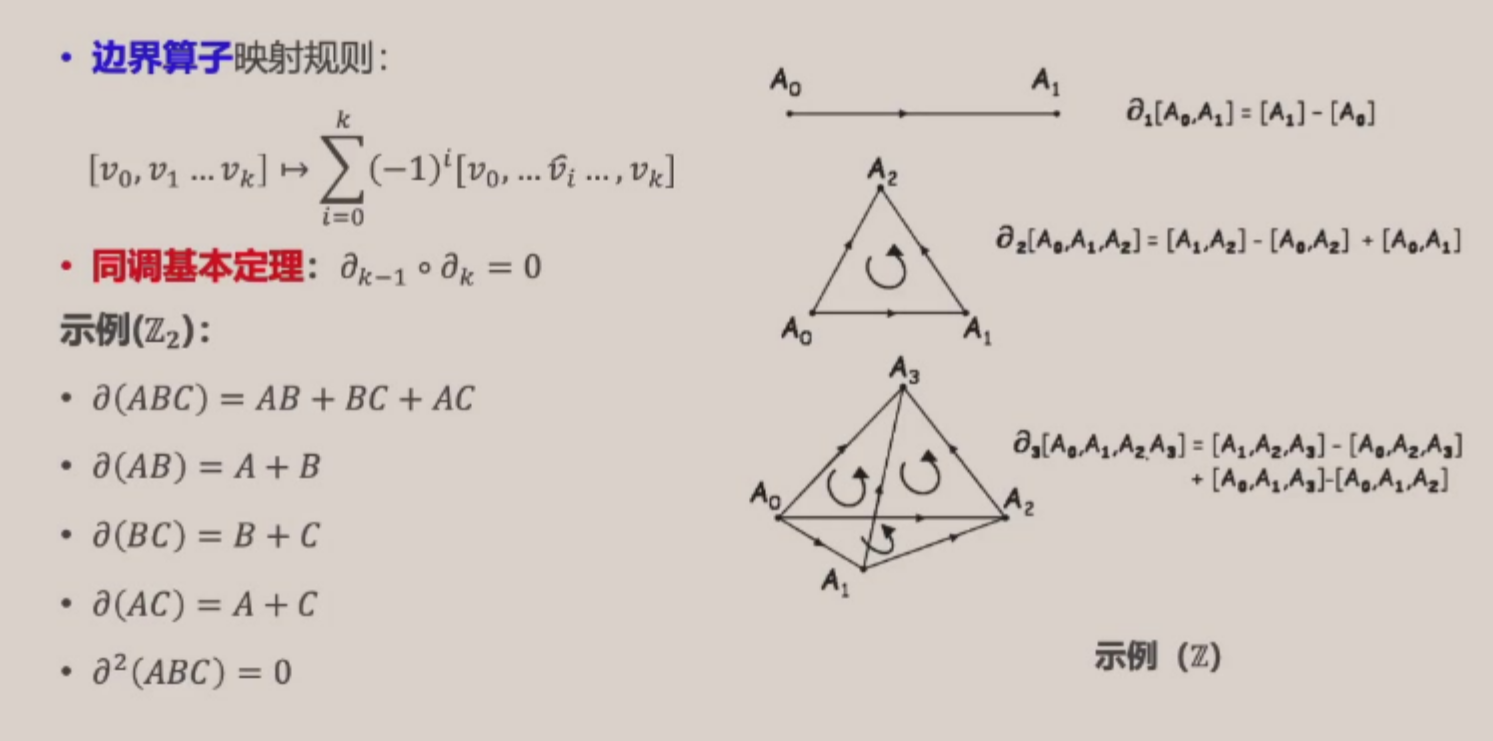
链复形¶

注意:
- 普遍意义上的同调群,不要求 \(\partial_\ast\) 是边界算子,只要求满足相邻两个的复合是零映射即可
- 当然,边界算子满足“相邻两个的复合式零映射”,因此边界算子可以用来构建一种特殊的同调群——链复形
- 其中,\(C_p\) 就是第 \(p\) 个链群;\(Z_p\) 就是 \(\ker\partial_p\);\(B_p\) 就是 \(\operatorname*{im}\partial_{p+1}\)
几何意义¶
我们称:
- \(Z_p\) 为闭链群,因为只有闭链,才能在映射只有变成 0(从而成为 \(\ker\))
- \(B_p\) 为边缘群,因为只有边缘,才能在对应一个更高维的拓扑结构(从而成为 \(\operatorname*{im}\))
不难发现,边缘必然是闭链,但是闭链未必是边缘(如下图,左侧是一个一般的闭链,但是它不是边缘。右侧是边缘,同时也是闭链)。因此,几何意义和上面的链复形的 \(B_p \trianglelefteq Z_p\)就对应起来了。
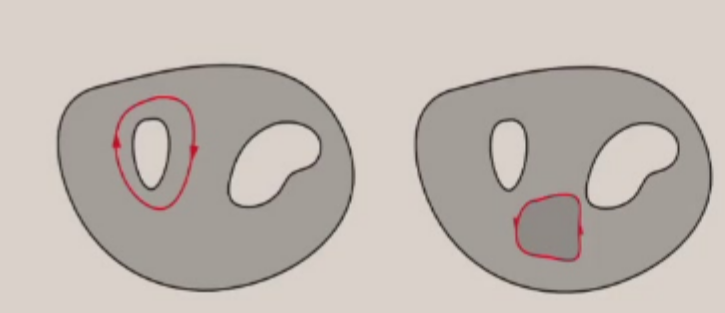
同调群¶

欧拉示性数¶
其中,\(i\) 指的是复形 \(K\) 中 \(i\) 维复形的数目
欧拉-庞加莱公式 $$ \chi(K) = \sum_{i=0}^\infty (-1)^i \beta_i $$ 其中,\(\beta_i := \dim H_k(X; \mathbb{Q})\) 就是贝蒂数。
其他同调群¶
以上定义同调群的方法,为单纯同调,单纯同调构造了一个从单纯形到交换群的桥梁。
此外,还有其他针对不同对象所构造的同调:
- 奇异同调 (Singular Homology):在拓扑空间上构造所谓的奇异单形,即连续映射 \(\sigma: \Delta^n \to X\),再利用奇异单形构造链复形得到拓扑空间 \(X\) 的奇异同调群
- 胞腔同调 (Cellular Homology):在比单纯复形更广义的CW复形上构造的同调
- 方形同调 (Cubical Homology):在方形阵列上构造的同调,在图像处理中经常使用
同调群计算¶
Smith 标准型¶
史密斯标准形(SNF)是适用于所有元素都位于主理想域(PID)的矩阵的标准形(不必是方阵) $$ \begin{pmatrix} \alpha_1 & 0 & 0 & & \cdots & & 0 & & \cdots & & 0 \ 0 & \alpha_2 & 0 & & \cdots & & 0 & & \cdots & & 0 \ 0 & 0 & \ddots & & & & 0 & & & & 0\ \vdots & & & \alpha_r & & & \vdots & & & & \vdots \ & & & & 0 & & \ & & & & & \ddots & \ 0 & & & \cdots & & & 0 & & \cdots & & 0 \end{pmatrix} $$ 其中,\(\forall 1 \leq i < r, \alpha_i | \alpha_{i+1}\)。
\(\mathbb Z_2\) 上的 Smith 标准型¶
由于 \(\mathbb Z_2 = \set{0,1}\),因此,对角线上只能是 0, 1。从而,就是 \(\alpha_1 = \alpha_2 = \dots = \alpha_r = 1\)。也就是: $$ \begin{pmatrix} 1 & 0 & 0 & & \cdots & & 0 & & \cdots & & 0 \ 0 & 1 & 0 & & \cdots & & 0 & & \cdots & & 0 \ 0 & 0 & \ddots & & & & 0 & & & & 0\ \vdots & & & 1 & & & \vdots & & & & \vdots \ & & & & 0 & & \ & & & & & \ddots & \ 0 & & & \cdots & & & 0 & & \cdots & & 0 \end{pmatrix} $$
\(\partial_k\) 的矩阵表达(关键概念)¶
不难发现,不管是 \(\mathbb Z\) 还是 \(\mathbb Z_2\),都是环(而且还是主理想整环),因此和所有 \(k\)-单形生成的链群本质上是一个主理想整环(有限生成)模。我们不妨直接使用矩阵来表示。
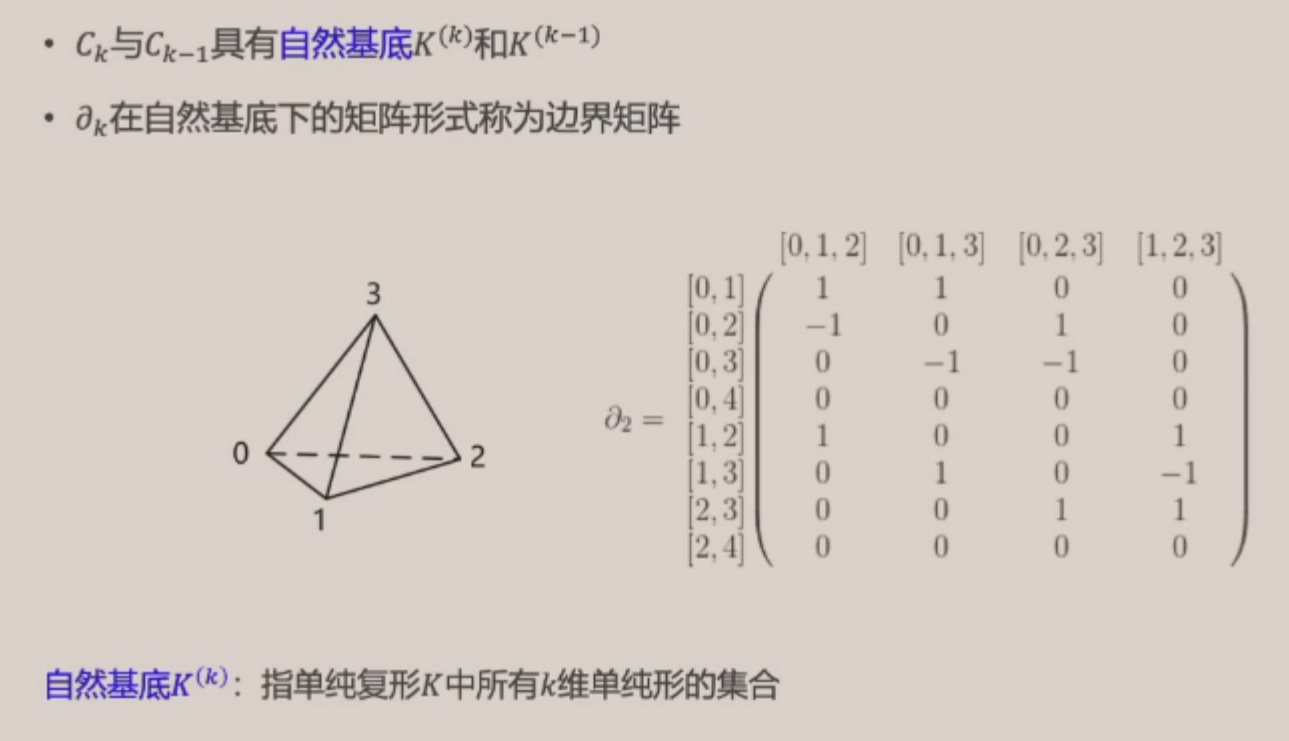
如上图所示:对于每一个链模 \(C_k\),我们不妨直接使用所有 \(k\)-单形作为其自然基底。然后就可以将 \(\partial_k\) 使用矩阵进行表达。
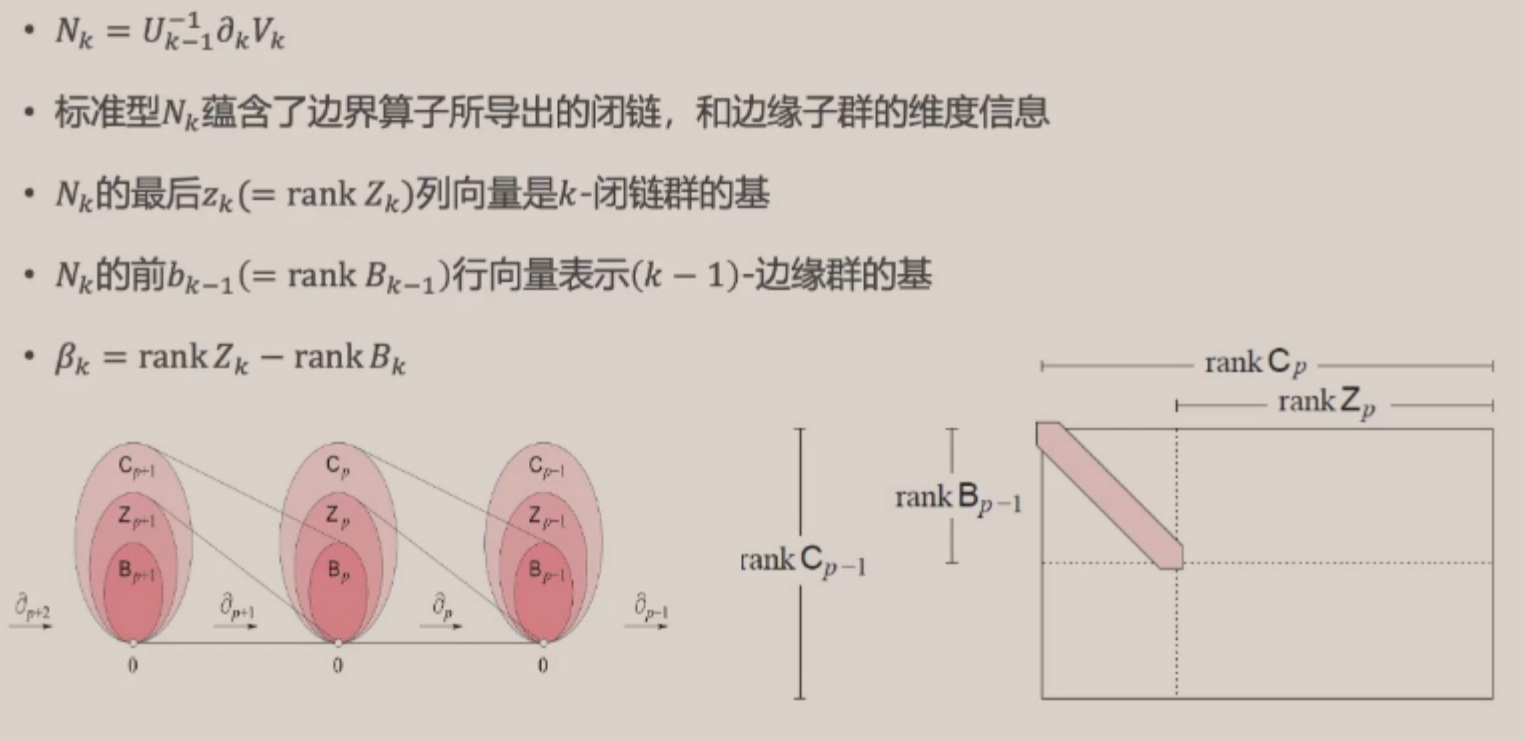
之后,我们可以将 \(\partial_k\) 转换成 Smith 标准形(如下图)
从而:
- 纵向的 ones 就是像空间——(k-1)-边缘群,i.e. \(B_{k-1}\)
- 横向的 zeros 就是核空间——k-闭链群,i.e. \(Z_k\)
基底转换¶
但是,不难发现,我们通过:
- \(N_k\) 求出 \(Z_k\)
- \(N_{k+1}\) 求出 \(B_k\)
但是,\(N_k\)(的横向基底)和 \(N_{k+1}\) (的纵向基底)不一定相同。因此,我们还需要进行基底的转换。
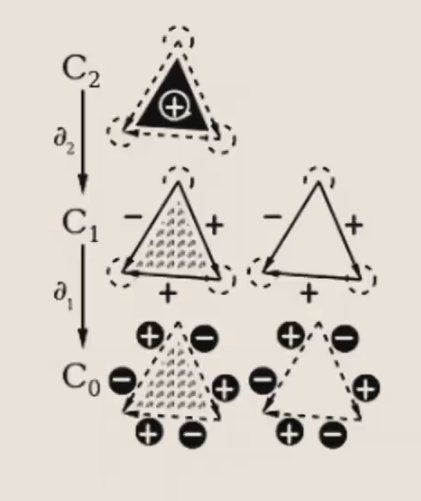
例子:正四面体¶

1. 求边界算子的矩阵¶
如图,我们以 \(\partial_1\) 为例(在 \(\mathbb Z_2\) 下):
由于 \(C_1\) 的基底就是:\(\set{ab, ac, ad, bc, bd, cd}\),而 \(C_0\) 是 \(\set{a, b, c, d}\),因此矩阵就是一个 4 × 6 的 $$ M(\partial_1) =\begin{bmatrix} 1 & 1 & 1 & 0 & 0 & 0 \ 1 & 0 & 0 & 1 & 1 & 0 \ 0 & 1 & 0 & 1 & 0 & 1 \ 0 & 0 & 1 & 0 & 1 & 1 \end{bmatrix} $$
- 比如,\(ab \to a + b\)
2. Smith 分解算法¶
然后,我们可以通过 \(\mathbb Z_2\) 上的 Smith 分解算法(此处略)来进行分解,得到: $$ \begin{aligned} &\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 & 0 & 0 \ 0 & 0 & 1 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \ = &U^{-1}M(\partial_1)V \ = &\begin{bmatrix} 1 & 0 & 0 & 0 \ 1 & 1 & 0 & 0 \ 1 & 1 & 1 & 0 \ 1 & 1 & 1 & 1 \end{bmatrix} M(\partial_1) \begin{bmatrix} 1 & 1 & 0 & 1 & 1 & 0 \ 0 & 1 & 1 & 1 & 0 & 1 \ 0 & 0 & 1 & 0 & 1 & 1 \ 0 & 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned} $$
- 其中:\(V\) 便是 Smith Normal Form (SNF) 的横向基,\(U\) 便是 Smith 标准型的纵向基。
3. 求出 1-单形的闭链群 \(Z_1\) 和 0-单形的边缘群 \(B_0\)¶
由于 SNF 的后三列为空,因此就是 \(Z_1\)。对应到 \(V\) 上,我们取后三列,就是: $$ \begin{bmatrix} 1 & 1 & 0 \ 1 & 0 & 1 \ 0 & 1 & 1 \ 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix} $$ 也就是: $$ \set{ab+ac+bc, ab+ad+bd, ac+ad+cd} $$ 不难发现,这就分别是正四面体的三个三角面片的三条边,而且第四个三角面片的三条边,可以由三个三角面片的三条边线性组合而成。符合直觉。
由于 SNF 的前三行不为空,因此就是 \(B_0\)。我们先求出 \(U\): $$ U = &\begin{bmatrix} 1 & 0 & 0 & 0 \ 1 & 1 & 0 & 0 \ 1 & 1 & 1 & 0 \ 1 & 1 & 1 & 1 \end{bmatrix}^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0 \ 1 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 \ 0 & 0 & 1 & 1 \ \end{bmatrix} $$
对应到 \(U\) 上,我们取前三列(注意:取列而不是取行),就是: $$ \begin{bmatrix} 1 & 0 & 0 \ 1 & 1 & 0 \ 0 & 1 & 1 \ 0 & 0 & 1 \ \end{bmatrix} $$ 也就是: $$ \set{a+b, b+c, c+d} $$ 正好与结果相对应。
不难发现,这就分别是正四面体的三条棱的顶点,而且另外三条棱的顶点也可以由其组合而成。符合直觉。
上同调与对偶¶
上同调¶
上同调就是同调的对偶,上同调的映射就是同调映射的对偶映射。
- 上链群:\(C^k(K) := C_k(K)^\ast\),也就是说,上链群就是链群的对偶空间
- 因此,上链就是作用在链群上的线性函数,也就是说作用在链群的自然基——单纯复形——上的任意函数
- 上边缘算子:\((\delta^k: C^k \to C^{k+1}) := (\partial_{k+1}: C_{k+1} \to C_k)^\ast\)
- 也就是说:上边缘算子,就是 \(\delta^k(\varphi)(x) := \varphi \circ \partial_{k+1}(x)\)
- 上边缘算子的直观解释:将作用在 k-复形的函数映射到了 k+1-复形的函数。至于 k+1-复形的函数如何计算?那还靠的是
- 首先将 k+1-复形通过边缘算子,映射为若干个 k-复形的线性组合
- 然后再用作用在 k-复形上的函数来计算
- 上边缘算子的图例如下图所示

- 上链复形:\(\dots \to C^{k-1} \to C^{k} \to C^{k+1} \to \dots\)
- 上闭链和上边缘:\(Z^k = \ker \delta^k, B^k = \im \delta^{k-1}\)
- 上闭链、上边缘和闭链、边缘的区别(可以发现两者就是类似于补空间的关系)
- 注意:下图的 \(B^k\) 其实是包含在 \(Z^k\) 里面的

- 上同调群:\(H^k = Z^k / B^k\)

例子¶

如上图,
- 它之所以是 1-上闭链,是因为:任何的 2-单形,经过边缘算子之后,所生成的 1-单形的线性组合,输入到这个 1-上闭链函数中,必然为 0。也就是说,这个 1-上闭链在 \(\delta^1\) 的零空间里
- 直观而言:就是图中任意的三角面片(i.e. 2-单形的基本单元),必然与这个单形有偶数个交“边”(i.e. 在 \(\mathbb Z_2\) 意义下,就等价于 0 个交“边”、不相交)
- 它之所以是 1-上边缘,是因为:一个将蓝色区域点映射为 0,红色区域点映射为 1 的 0-上闭链,可以通过 \(\delta^0\) 映射成这个 1-上闭链。也就是说,这个 1-上闭链在 \(\delta^0\) 的像空间里
- 直观而言:就是图中的黑色边,都是蓝色区域和红色区域的跨边
- 另外,直观而言:由于所有三角面片经过两次 \(\partial\) 之后,都会变成 2 × (3 个顶点) ≡ 0 × (3 个顶点) ≡ 0,因此,\(\delta^{k}\circ\delta^{k-1} \equiv 0\),也就是说,必然有 \(B_k \subseteq Z_k\)。
上边缘矩阵¶
由于上边缘算子是边缘算子的对偶映射,自然,上边缘矩阵就是边缘矩阵的 Hermitian 转置:\(M(\delta^k) := M(\partial_{k+1})\)。

另外,不难发现,同调群和上同调群是同构的。
- 毕竟 \(\rank H^i = \rank Z^k - \rank B^k = (\rank C_p - \rank B_k) - (\rank C_p - \rank Z_k) = \rank Z_k - \rank B_k = rank H_i\)
对偶块¶
重心细分¶

具体解释:

对偶块的建立¶

简单来说,就是:
- 对于目标单形 \(\sigma \in K\),我们先找出其重心
- 然后找出在 \(\operatorname*{Sd} K\) 中所有与它的重心相连的单形
- 对于每一个与它的重心相连的单形,我们取出这个单形的所有顶点
- 对于这个单形的每个顶点,它必须是由一个维数不小于 \(\dim \sigma\) 的 K 中的单形所生成