5. Iterative Techniques in Matrix Algebra
本章思路
为了研究矩阵的不动点迭代能否收敛,我们需要研究矩阵的“收敛性”问题:如果一个矩阵的无穷次幂等于零矩阵,则称这个矩阵收敛。
通过谱半径(以及若尔当标准型),很容易证明谱半径小于 1 是矩阵收敛的充要条件。
但是,由于谱半径有以下两个缺点:
- 不是随便求就能求出来的
- 对于非可对角化的矩阵而言,不好判断收敛速率
因此,我们就转而研究一个谱半径近似替代品——矩阵范数,因为容易求出,且具有良好的性质。
Norm¶
Vector Norm¶
范数很简单,对于向量范数,只需要满足:
- \(\| x \| \geq 0\) 且 \(\| x \| = 0 \iff x = 0\) (positive definite)
- \(\|\alpha x \| = \abs{\alpha} \| x \|\) (homogeneous)
- \(\| x + y \| \leq \| x \| + \| y \|\) (triangle inequality)
即可。
Converge w.r.t Norm¶

如图,
- 我们可以容易证明,无穷范数收敛等价于逐 element 收敛。
- 我们又通过证明所有 \(\R^n\) 的范数等价,因此任意范数收敛等价于逐 element 收敛。
证明 (2):
我们不妨证明所有范数与 \(l^1\) 范数等价。
对于 \(C_2\) 而言,证明是显然的。我们只需要找到自然基下的所有 \(C_{2}^{(i)}\) 即可,然后取最大值。
- \(\| x \|_A \leq \sum_{i=1}^N \| x_i \|_A = \sum_{i=1}^N \| x_i \|_A \leq \sum_{i=1}^N \abs{x_i}_A \max(C_2^{(i)}) = \max(C_2^{(i)}) \| x \|_1\)。
对于 \(C_1\) 而言,我们可以使用 Bolzano-Weierstrass 方法证明:
假设不存在这样的 \(C_1\),那么, $$ \forall n \in \mathbb{N}, \exists x(n) \in \R^n, s.t. |x(n)|_1 = 1: \frac 1 n = \frac 1 n |x(n)|_1 > |x(n)|_A $$ 从而:\(\lim_{n \to \infty} \|x(n)\|_A = 0\)。由于 \(\|x(n)\|_1 = 1 \implies x(n) \text{ is bounded}\),由 Bolzano-Weierstrass 定理可知:存在收敛子列,这个收敛子列必然收敛至 \(x^*\)。
再由范数的连续性(易证)可知:\(\|x^*\|_A = \| \lim_{i \to \infty}x(n_i)\|_A = \lim_{i \to \infty} \|x(n_i)\|_A = 0\)。
因此,我们的反证法分三大步:
- 向量的值收敛于 0
- 向量(的一个子列)收敛
- 由范数函数的连续性:向量(的一个子列)的收敛点的值等于 0,与 positive definite 矛盾
Matrix Norm¶
对于矩阵范数,需要满足:
- \(\| A \| \geq 0\) 且 \(\| A \| = 0 \iff x = 0\) (positive definite)
- \(\|\alpha A \| = \abs{\alpha} \| A \|\) (homogeneous)
- \(\| A + B \| \leq \| A \| + \| B \|\) (triangle inequality)
- \(\| AB \| \leq \| A \| \| B \|\) (consistency)
注意第四点是矩阵范数独有的。
Some Popular Norms¶
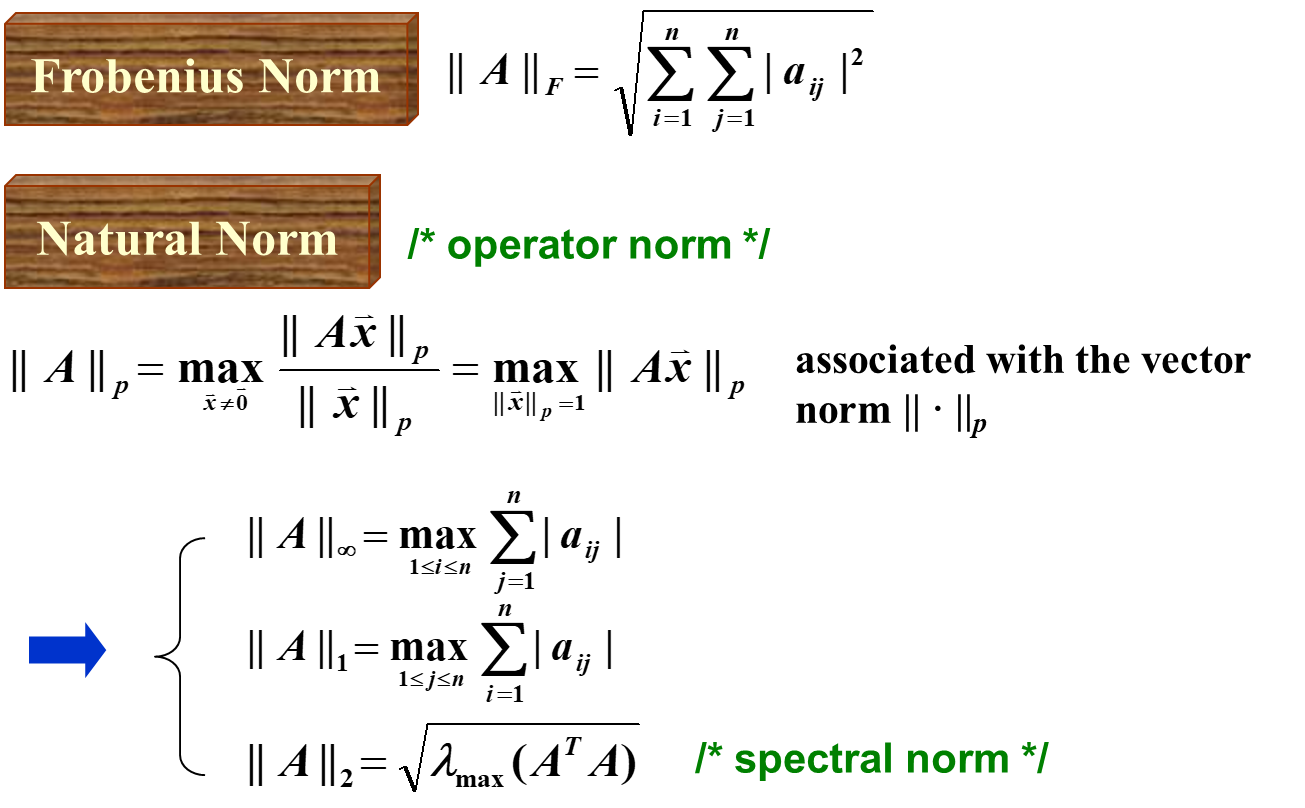
第一个 Frobenius Norm 形式上简单,但是数学上解释复杂。
第二个 Natural Norm 是通过向量范数诱导的,形式上略复杂,但是数学上很简单。
对于常见的向量范数,对应的矩阵范数如下:
- 无穷范数:逐列相加,取最大的那一行
- 1-范数:逐行相加,取最大的那一列
- 2-范数:对于一个高维球面,我们对其进行线性变换,然后取其最长轴。或者就是取矩阵最大的奇异值。
Eigenvalues and Eigenvectors¶
Spectral Radius¶
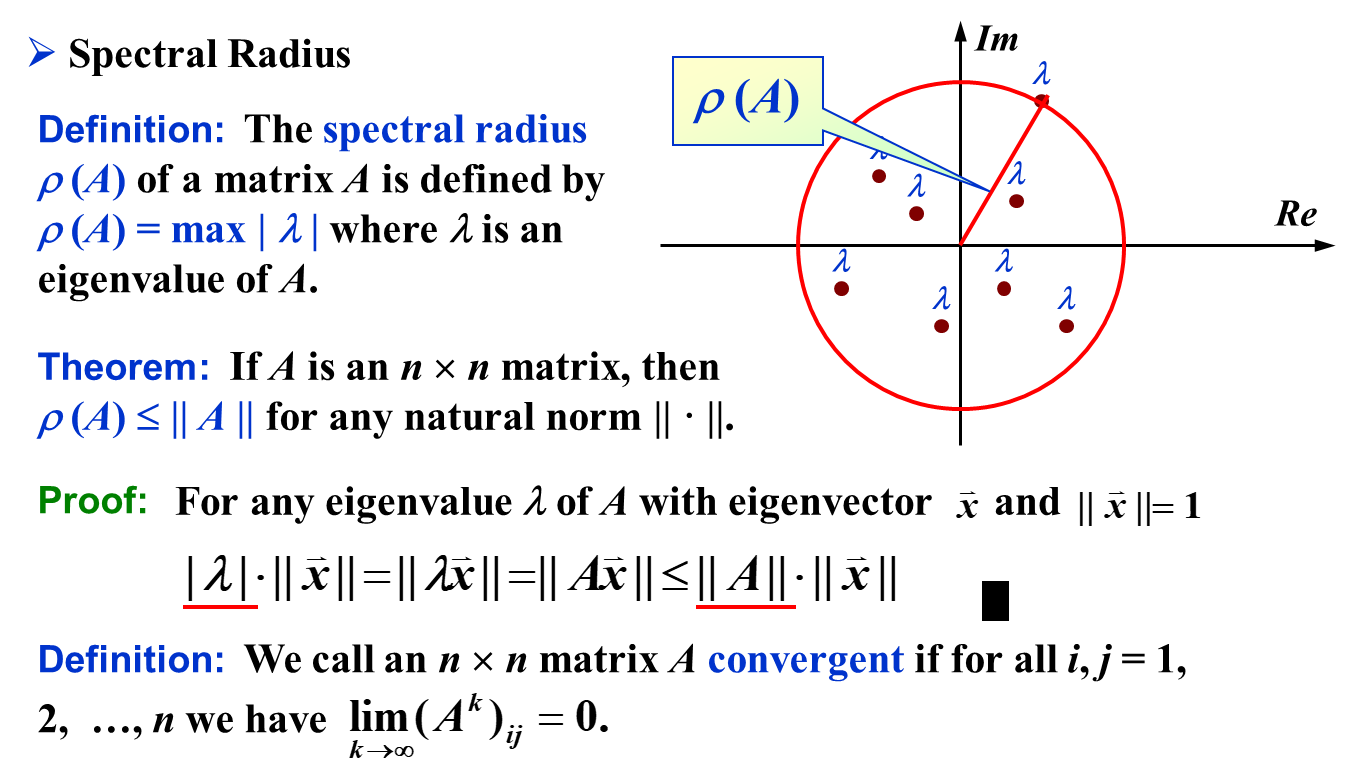
Well-definedness
由于代数闭域上的方阵一定有至少一个 eigenvalue,因为:
$$ f(\lambda) = \det(A - \lambda I) $$ 是一个多项式。而多项式在代数闭域上必然有根,因此必然有只要一个 eigenvlaue。因此,\(\rho(A)\) 是良定义的。
重要的定理是:对于任意的 natural norm,矩阵的谱半径一定不大于 natural norm。
Convergence of Matrix w.r.t its norm¶
对于实对称矩阵,我们可以直接 Orthonormal Decomposition,结论更加简单。如果矩阵的特征值的绝对值均小于 1,那么就收敛。
更一般地,如下图,任意矩阵都可以分解成若尔当标准型。其中一个若尔当块如图所示。
同时,不难证明,若尔当型收敛 iff \(\abs{\lambda} < 1\)。因此只要所有特征值的绝对值小于 1,矩阵就收敛
Iterative Techniques¶
Jacobi Method¶
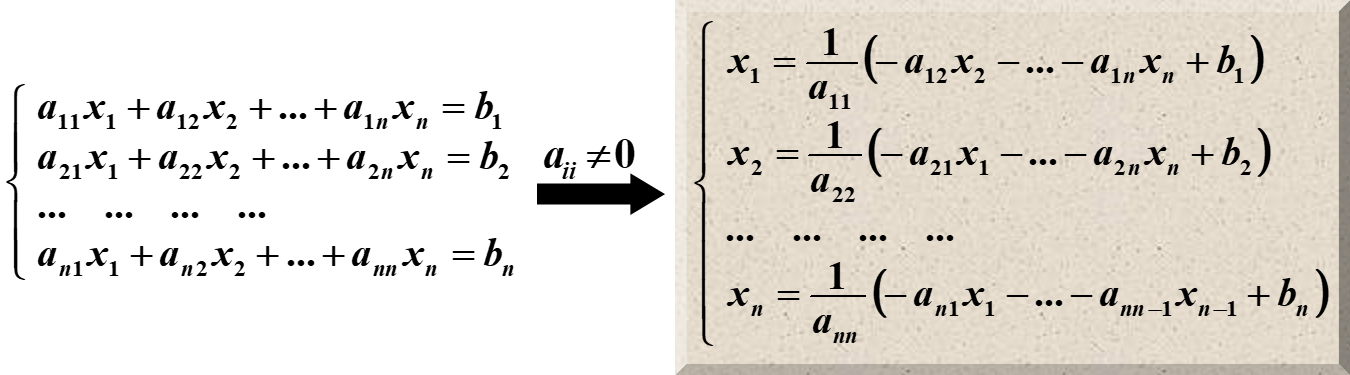
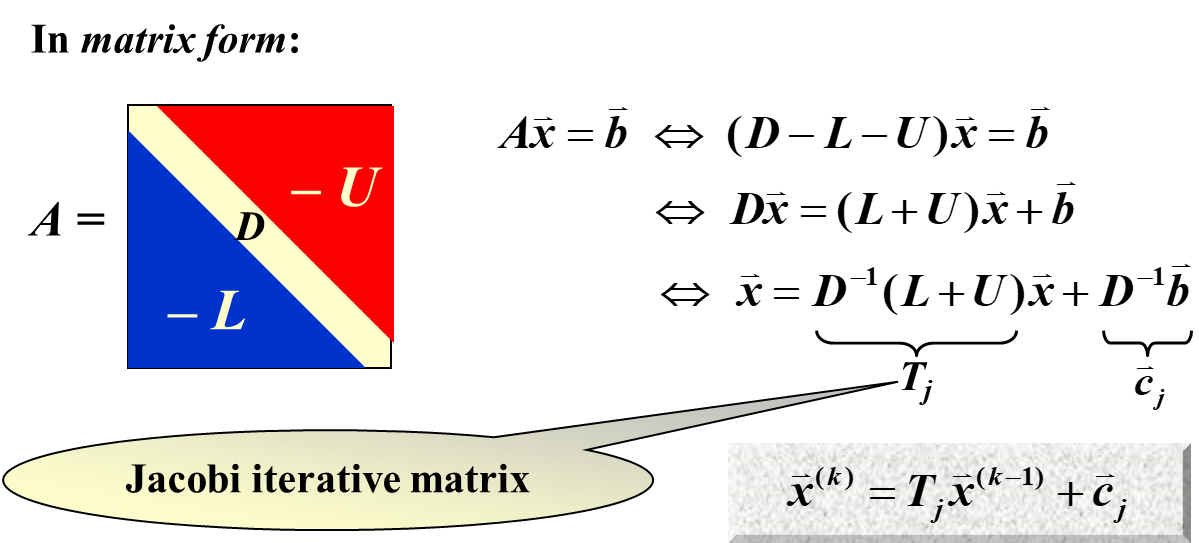
我们在这里,用的也是类似于不动点迭代的方法。
举例¶
一个形如 的线性方程,估计初始:
我们用上文描述的方程来估计。首先,将等式写为以方便计算,其中和。注意 中的 和是的严格 递增和递减部分。变成如下数值:
令 as
解出C为:
用计算出来的T和C,我们估计为
继续迭代得:
这个过程一直重复直到收敛(直到足够小)。这个例子在25次迭代之后的解是
Gauss-Seidal Method¶
Gauss-Seidal 方法,在形式上,上和 Jacobi 方法的区别不大。
- 但是 Gauss-Seidal 比较难并行化,因为每计算一个 \(x_j^{(k)}\) 都要用到之前的 \(x_{j-1}^{(k)}, x_{j-2}^{(k)}, \dots\)。
Comparison¶
如图,左侧是 Gauss - Seidel 方法,右侧是 Jacobi 方法。两者最大的不同,就是 Gauss - Seidel 方法,总是使用最新的数据。

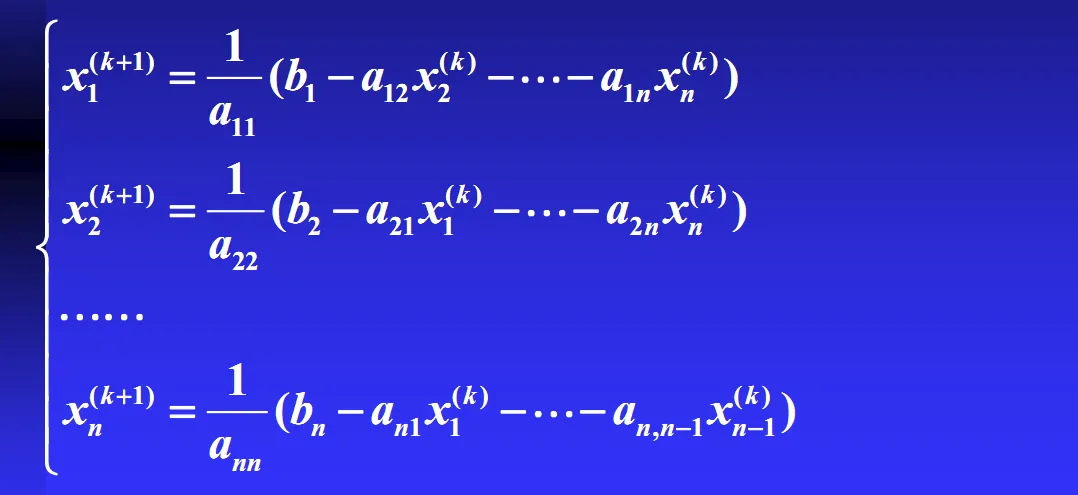
Convergence: Proof¶
标准的收敛情况,是 \(T_j = D^{-1}(L+U)\) 的谱半径小于 1。
证明:
我们令第 \(k\) 轮的误差为 \(\vec e^{(k)}\)

这个误差,本质上,就是向量值多元函数的不动点迭代法。
因此,如果我们希望误差收敛,就必须要求 \(T\) 本身就是收敛的。而 \(T\) 是收敛的条件,就是谱半径小于 1(上文已经证明)。
Other convergence conditions¶
保证收敛的条件还可以是矩阵 \(A\) 为严格或不可约地对角占优矩阵。不过,有时即使不满足此条件,雅可比法仍可收敛。
其中,如果是严格对角线占优,证明如下:
我们可以得到 \(\lambda I - T = \lambda D^{-1} D - D^{-1} (L + U) = D^{-1} (\lambda D - (L + U))\)。
不难发现,如果\(\lambda \geq 1\),那么 \(\lambda D - (L + U)\) 仍然是严格对角线占优,也就是可逆,从而 \(\lambda I - T\) 可逆,从而 \(\lambda\) 不可能是 \(T\) 的 eigenvalue。
因此,\(\rho(T) < 1\)。
Error Bound Estimation¶
矩阵的 normal norm 相比谱半径更适合用来估计误差。
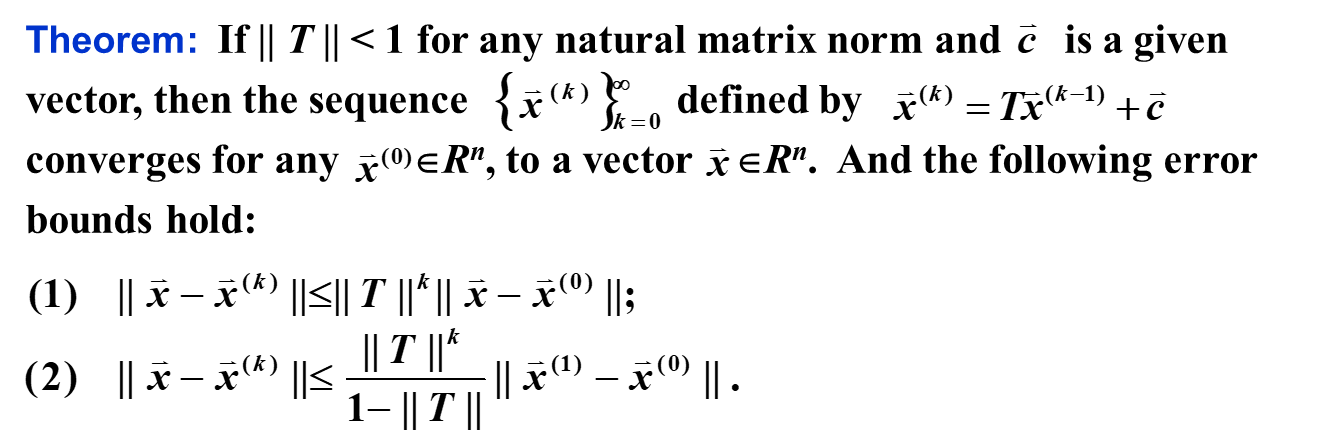
由于谱半径小于等于任意的自然范数,因此: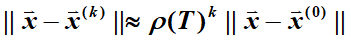
Conditional Number¶
推导¶

求 \(K(A)\)¶
由于 \(K(A) = \|A\| \|A^{-1}\|\),因此,一般而言,我们需要求出 \(A^{-1}\) 才行。但是我们并不希望使用 \(\mathcal O(n^{\log_2 7})\) 的复杂度来求逆矩阵。
Note:
- If \(A\) is symmetric, then \(K(A)_2 = \frac {\max \abs{\lambda}} {\min \abs{\lambda}}\)
- 这是因为,\(A\) 可以标正对角化 ⇒ \(A\) 的特征值的模和奇异值相等
- 另外,实际上,只需要 \(A\) 是 normal operator, i.e. \(A A^t = A^t A\),就可以标正对角化,从而就可以套用在这里
- \(K(A)_p \geq 1\) for all natural norm \(\|\cdot\|_p\)
- 因为,\(\|A\| \geq \|Ax\| / \|x\|\), \(\|A^{-1}\| \geq \|A^{-1}Ax\| / \|Ax\| := \|x\| / \|Ax\|\)
- \(K(\alpha A) = K(A)\)
- 易证
- 也就是说,\(A\) 的矩阵范数和其放大倍率无关
- \(K(A)_2 = 1\) if \(A\) is orthogonal, i.e. \(A^{-1} = A^t\)
- orthogonality ⇒ \(\forall x: \|Ax\| = \|x\|\) ⇒ \(\|A\|=1\), and so is \(\|A^{-1}\|\)
- \(K(RA)_2 = K(AR)_2 = K(A)_2\), if \(R\) is orthogonal
总结:
- 对称矩阵(乃至正规矩阵)直接算
- 任意矩阵的条件数都不小于 1
- 条件数就是相对误差的放大倍率。但是相对误差是无法减小的,因此条件数至少是 1。
- 条件数与常数放缩无关
- 正交矩阵的条件数就是 1