Skip to content

Error Analysis for Iterative Methods

Definition: Suppose \(\set{p_n} (n=0,1,2,\dots)\) is a sequence that converges to \(p\), with \(p_n \neq p\) for all \(n\). If positive constants \(\alpha\) and \(\lambda\) exist with $$ \lim_{n\to\infty} \frac{\lvert p_{n+1} - p \rvert}{\lvert p_n - p \rvert^\alpha} = \lambda $$ then \(\set {p_n} (n=0,1,2,\dots)\) converges to \(p\) of order \(\alpha\), with asymptotic error constant \(\lambda\).

  1. If \(\alpha = 1\), the sequence is linearly convergent
  2. If \(\alpha = 2\), the sequence is quadratically convergent

Newton's Method: Revisited

Analysis of Convergence

牛顿法就是： $$ p_{n+1} = p_n - \frac {f(p_n)} {f'(p_n)} $$ 通过 Taylor's Method: $$ 0 = f(p) = f(p_n) + f'(p_n) (p - p_n) + \frac 1 2 f''(\xi_n)(p - p_n)^2 $$ 因此： $$ p = p_n - \frac {f(p_n)} {f'(p_n)} - \frac {f''(\xi_n)} {2! f'(p_n)} (p-p_n)^2 = p_{n+1} - \frac {f''(\xi_n)} {2! f'(p_n)} (p-p_n)^2 $$ 从而： $$ \frac{\lvert p_{n+1} - p \rvert}{\lvert p_n - p \rvert^2} = \frac {\frac {f''(\xi_n)} {2! f'(p_n)} (p-p_n)^2} {(p - p_n)^2} = \frac {f''(\xi_n)} {2 f'(p_n)} $$

  • As long as \(f'(p) \neq 0\), Newton's method is AT LEAST quadratically convergent

NOTE:

  1. For general fixed point method, this doesn't hold - it can be as bad as linearly convergent.
  2. If the root is a simple root, it guarantees fast convergence locally, not globally. Thus you have to try multiple initial values (i.e. \(p_0\)) to get the correct answer, and also make sure the multiplicity of the root is 1.

Sidenote: How much time do I need with different α?

假设一次迭代的耗时为 \(t\)，我们的期望精度为 \(eps\)，初始误差为 \(e_0\)。

又假设 \(\frac{e_{n+1}}{e_n^\alpha} = \frac{\lvert p_{n+1} - p \rvert}{\lvert p_n - p \rvert^\alpha} \approx \lambda, \alpha > 1\)，那么 $$ \ln e_{n+1} \approx \ln \lambda + \alpha \ln e_n \iff \ln e_{n+1} + \frac 1 {\alpha - 1} \ln \lambda \approx \alpha (\ln e_n + \frac 1 {\alpha - 1} \ln \lambda) $$ 从而： $$ \alpha^{\frac T t} (\ln e_n + \frac 1 {\alpha - 1} \ln \lambda) \approx \ln eps + \frac 1 {\alpha - 1} \ln \lambda $$ 也就是说： $$ T \approx \frac{\ln(-(\ln eps + \frac 1 {\alpha - 1} \ln \lambda)) - \ln(-(\ln e_n + \frac 1 {\alpha - 1} \ln \lambda))}{\ln \alpha} t = \mathcal O(\frac{\ln\ln eps} {\ln \alpha}t) $$

  • 当然，如果 \(\alpha = 1\)，那么 \(e_0 \lambda^{\frac T t} = eps \implies T = \frac{\ln eps - \ln e_0}{\ln \lambda}t\)

假如 \(\lambda_1 = 0.5, \lambda_2 = 0.8\)，\(\alpha_1 = 1, \alpha_2 = 2\)，\(e_n = 10^{-1}, eps = 10^{-10}, t = 1 \text{ hr}\)，那么，

使用如下函数：

from math import *

def T_not_one(eps, a, l, e0, t):
    eps_ln = log(-(log(eps) + 1 / (a - 1) * log(l)))
    e0_ln = log(-(log(e0) + 1 / (a - 1) * log(l)))
    return (eps_ln - e0_ln) / log(a) * t


def T(eps, a, l, e0, t):
    if (a != 1):
            return T_not_one(eps, a, l, e0, t)
    else:
            return t * (log(eps) - log(e0)) / log(l)


l1, l2 = 0.9, 0.9
a1, a2 = 1, 2
e0 = 1e-1
eps = 1e-12
t = 1

T1, T2 = T(eps, a1, l1, e0, t), T(eps, a2, l2, e0, t)
day1, day2 = floor(T1 / 24), floor(T2 / 24)
hr1, hr2 = T1 - day1 * 24, T2 - day2 * 24

print(f"T1: {day1} days and {hr1:.1f} hours")
print(f"T2: {day2} days and {hr2:.1f} hours")

结果：

T1: 10 days and 0.4 hours
T2: 0 days and 3.5 hours

可见两者的差距很大。特别地，\(\alpha = 2\) 的时候，总用时对 \(\lambda, eps\) 其实并不太敏感（因为都是 \(\ln\ln\)）；而 \(\alpha = 1\) 的时候，对 \(eps\) 和 \(\lambda\) 其实很敏感。

Sidenote: General Practical Method for Determine α and λ

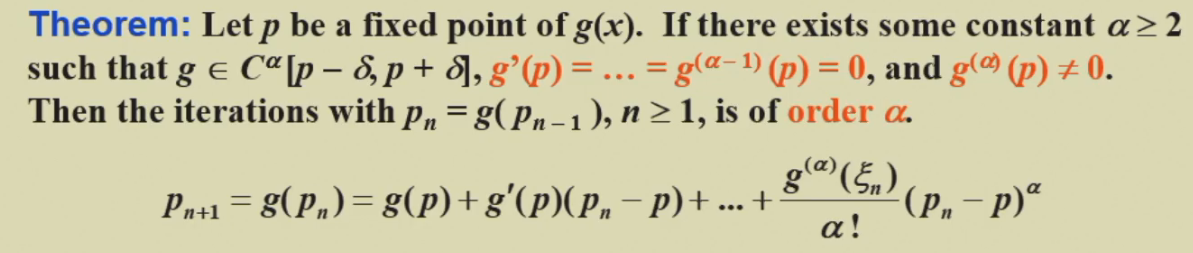
image-20240313112142789

  • 证明：由于 \(g(p) = p\)，上式也就是：\(p_{n+1} - p = \frac {g^{\alpha}(\xi_n)} {\alpha !} (p_n - p) ^\alpha\)，从而易证。

以牛顿法为例： $$ g(x) = x - \frac{f(x)}{f'(x)} $$ 因此： $$ \lim_{x\to x_0}g'(x) = \frac{f(x_0)f''(x_0)}{f'(x_0)^2} =0 \quad \text{ (as long as } f'(x_0) \neq 0) $$ 又因为： $$ g''(x) = \frac{f{\left(x \right)} \frac{d^{3}}{d x^{3}} f{\left(x \right)}}{\left(\frac{d}{d x} f{\left(x \right)}\right)^{2}} - \frac{2 f{\left(x \right)} \left(\frac{d^{2}}{d x^{2}} f{\left(x \right)}\right)^{2}}{\left(\frac{d}{d x} f{\left(x \right)}\right)^{3}} + \frac{\frac{d^{2}}{d x^{2}} f{\left(x \right)}}{\frac{d}{d x} f{\left(x \right)}} $$ 由于 \(f''(x_0)\) 一般并不为 0，所以 \(g''(x_0)\) 一般也不为 0，所以一般 \(\alpha = 2\)。和我们之前的结果一样。

Problem With Multiple Roots

对于 \(k\) 重根的情况：

$$ \begin{aligned} &f(x) = (x-x_0)^kq(x) \newline \implies &f'(x) = k(x-x_0)^{k-1} q(x) + (x-x_0)^{k}q'(x) \newline \implies& f'(x_0) = \begin{cases} 0 \quad \text{if }k \geq 2 \newline q(x_0) \neq 0 \quad \text{if } k = 1 \end{cases} \end{aligned} $$ 因此，对于多重根的情况，牛顿迭代法的性能会迅速下降。

  • 具体地，如果有多重根，那么牛顿法的 \(\alpha = 1\)，而且 \(\lambda = \frac{g'(p)}{1!} = 1 - \frac 1 k < 1\)，因此虽然收敛，但是只是 1 阶收敛，而且随着 \(k\) 的增加，收敛时间会近似线性增加（i.e. \(-\frac 1 {\ln \lambda} = -\frac 1 {\ln (1 - \frac 1 k)} \approx k\)）。

如何处理这样的问题呢？可以使用 modified version（如下）。

Modified Newton's Method

我们令 \(\mu(x) = \frac {f(x)} {f'(x)}\)，从而 \(g(x) = x - \frac{\mu(x)}{\mu'(x)} = x - \frac{f(x)f'(x)}{[f'(x)]^2 -f(x)f''(x)}\)

如果 \(f(x) = (x-x_n)^kq(x)\)，而且 \(q(x_n) \neq 0\)那么： $$ \begin{aligned} &\mu(x) = \frac{(x-x_n)^kq(x)}{k(x-x_n)^{k-1}q(x) + (x-x_n)^{k}q'(x)} = \frac{(x-x_n)q(x)}{kq(x) + (x-x_n)q'(x)} \newline \implies &\mu'(x) = \frac{[q(x) + (x-x_n)q'(x)][kq(x) + (x-x_n)q'(x)] - [(k+1)q'(x) + (x-x_n)q''(x)][(x-x_n)q(x)]}{\left[kq(x) + (x-x_n)q'(x)\right]^2} \newline \implies &\mu'(x_n) = \frac{kq^2(x_n)}{k^2q^2(x_n)} = \frac{1}{k} \end{aligned} $$ 从而，满足了 \(\mu'(x_0) \neq 0\) 的性质，使得迭代速率仍然可以为二阶。

Problems:

  1. 需要额外计算 \(f''(x)\)
  2. 由于 \([f'(x)]^2 -f(x)f''(x)\) 是两个很小的数相减，因此当两者接近的时候，relative rounding error 就会非常大。

Accelerating Methods

Aitken's Δ2 Method

Intuition

由于 $$ \frac { p _ { n + 1 } - p } { p _ { n } - p } \approx \lambda \newline \frac { p _ { n + 2 } - p } { p _ { n + 1 } - p } \approx \lambda $$

因此，直觉上，两个式子应该也“差不多”。

\[ \begin{aligned} \frac { p _ { n + 1 } - p } { p _ { n } - p } &\approx \frac { p _ { n + 2 } - p } { p _ { n + 1 } - p } \newline ( p _ { n + 1 } - p ) ( p _ { n + 1 } - p ) &\approx ( p _ { n + 2 } - p ) ( p _ { n } - p ) \newline p _ { n + 1 } ^ { 2 } - 2 p _ { n + 1 } p + p ^ { 2 } &\approx p _ { n + 2 } p _ { n } - ( p _ { n + 2 } + p _ { n } ) p + p ^ { 2 } \newline - 2 p _ { n + 1 } p + ( p _ { n + 2 } + p _ { n } ) p &\approx p _ { n + 2 } p _ { n } - p _ { n + 1 } ^ { 2 } \newline p &\approx \frac { p _ { n + 2 } p _ { n } - p _ { n + 1 } ^ { 2 } } { - 2 p _ { n + 1 } + ( p _ { n + 2 } + p _ { n } ) } \newline p &\approx p _ { n } - \frac { ( p _ { n + 1 } - p _ { n } ) ^ { 2 } } { p _ { n + 2 } - 2 p _ { n + 1 } + p _ { n } } \end{aligned} \]

从而，我们得到了一个关于 \(p\) 的 intuitive 的式子。我们不妨就直接用右边的式子代替 \(g(x)\)：

\[ \widehat p_n = p _ { n } - \frac { ( p _ { n + 1 } - p _ { n } ) ^ { 2 } } { p _ { n + 2 } - 2 p _ { n + 1 } + p _ { n } } \]

Definition

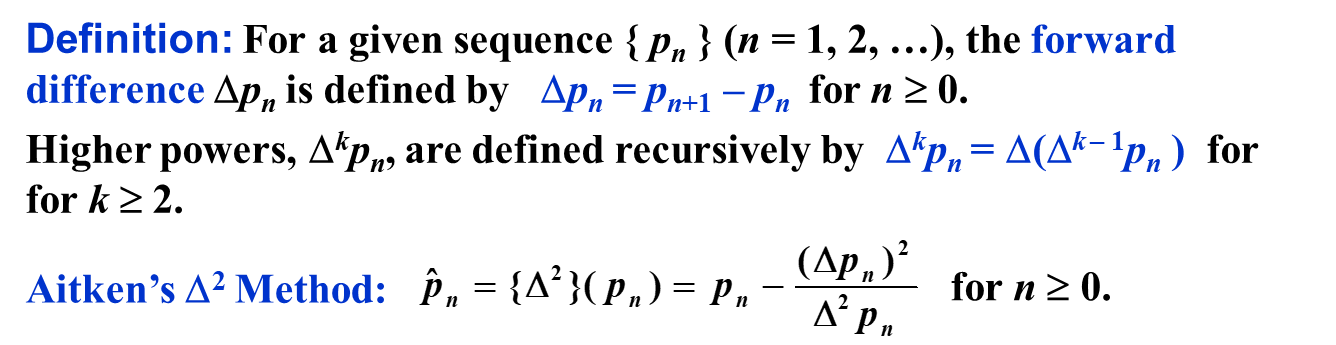
image-20240313152716120

Calculation Steps

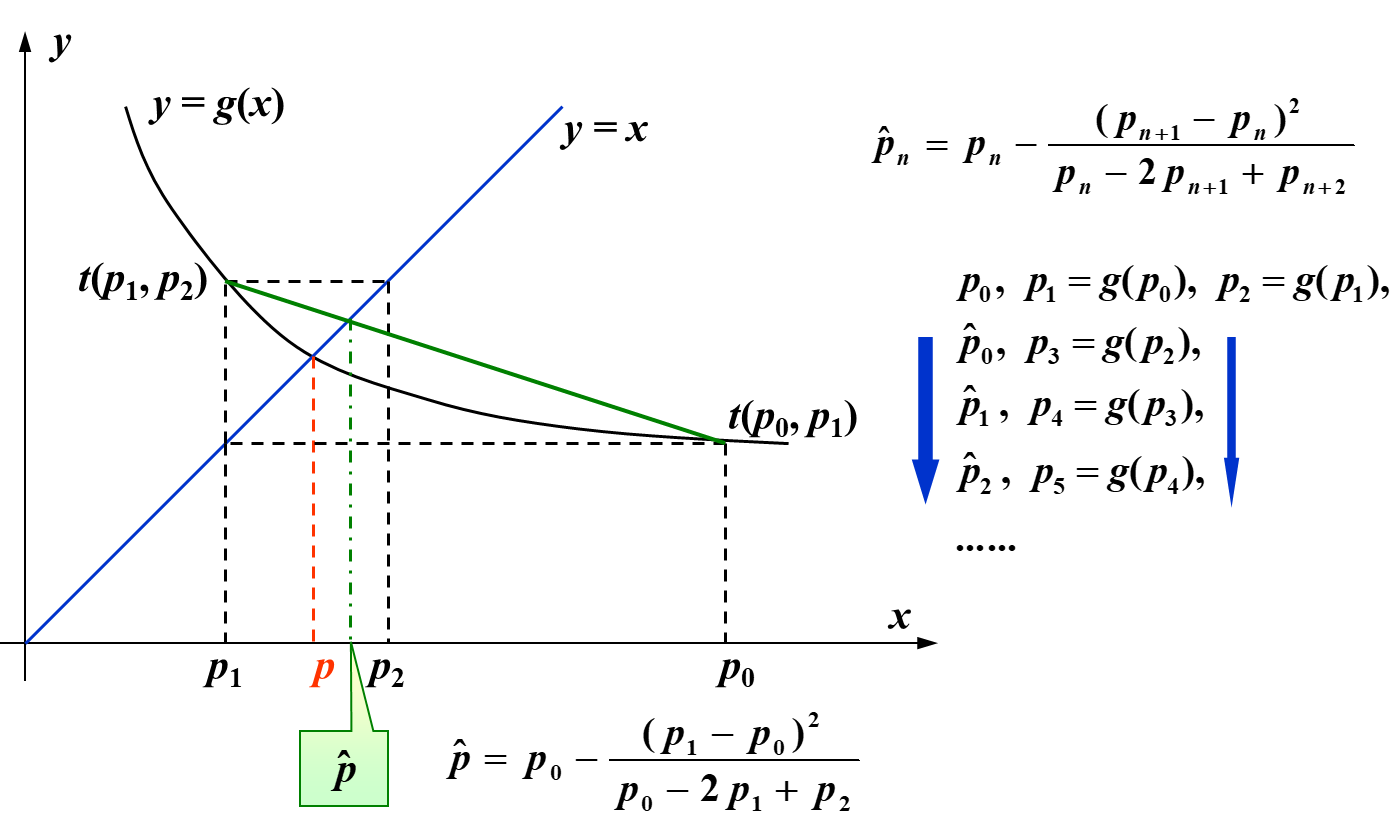
  1. 首先算出 \(\set{p_0, p_1, \dots}\)
  2. 然后通过 \(p_i, p_{i+1}, p_{i + 2}\) 算出 \(\widehat p_{i}\)
  3. 我们用 \(\widehat p_n\) 代替 \(p_n\) 作为最后的输出

下图就是形象的计算过程：

image-20240313151913805

WARNING:

  1. 不可以认为 \(\widehat p_n\) 比 \(p_n\) “精确”，就自作聪明，在 \(\widehat p_n\) 算出来之后，再反过来通过它来计算 \(p_{n+1}, p_{n+2}, p_{n+3}\)（e.g. \(p_4 = g(g(g(\widehat p_1)))\)，而非 \(p_4 = g(p_3)\)）。因为 \(\widehat p_n\) 更加精确某种意义上来说，是“概率性”的、“不可预知”的，因此不能混用。
  2. 递归计算不能够无限优化，i.e. \(\set{\widehat {\widehat p}_n}, \set{\widehat {\widehat {\widehat p}}_n}, \dots\) 的收敛性并不会趋于无穷大。这就像多次压缩文件无法使其变成 1 byte 一样。

Analysis

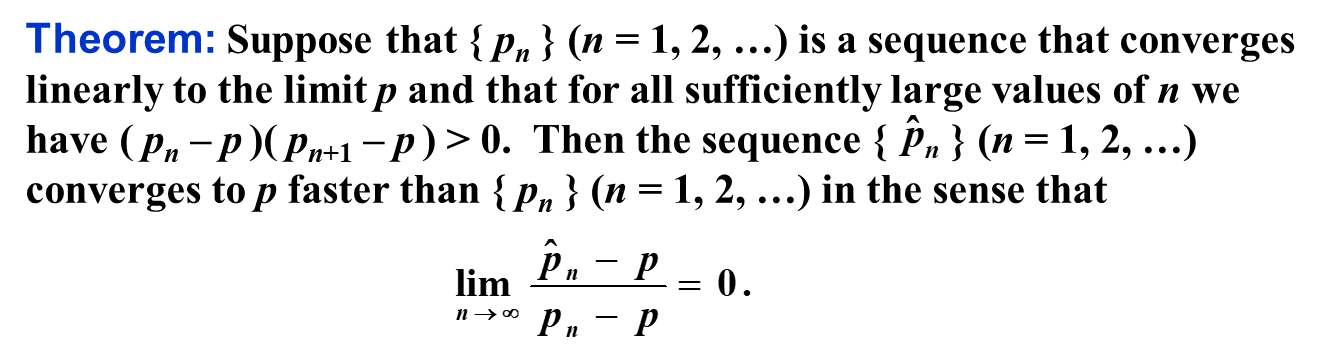
image-20240313155245679

Steffensen’s Method

Note

就是三个一组的反复加深式的 Aitken's Δ2 Method。

  • 颇有 Romberg Integration (见 Lec 9: approximation theory) 这种将梯形近似反复精细化的味道。

虽然 Aitken's Δ2 Method 不可以混用，但是，不能混用的原因是混用可能会导致 \(\set{p_n}\) 不再是线性数列。

Aitken's Δ2 Method 最少需要 3 个数来计算出来 \(\widehat p_0\)，因此，我们可以三个一组，每组均采用递推的方法计算（保证是线性数列），然后得到 \(\widehat p_0\)，当作”新的起点“，然后再用 \(\widehat p_0\) 继续这样做，so on and so forth。

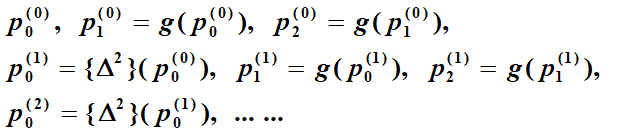
image-20240313155847725

形象地看，如下图，序列整体不是线性的，但是每个方框内的小序列是线性的。箭头指的是用前一个方框的三个值，推出新的方框的第一个值。

image-20240313160216435

由于方框内均为线性以及层层地推，由归纳法可知，所有方框均比上一个更优。

  • 实际上，如果 \(g'(p) \neq 1\)，则这样的迭代满足 local quadratic convergence。

Direct Method for Solving Linear Systems

定义：解形如 \(A\mathbf x=B\) 这样的线性方程组

Amount of Computation

由于

  1. 单个乘除计算的 cycle 较多
  2. 乘除对数值稳定性的破坏性较大

我们在分析线性系统的数值算法的时候，只考虑乘除运算的数量。

Example: Gaussian Elimination

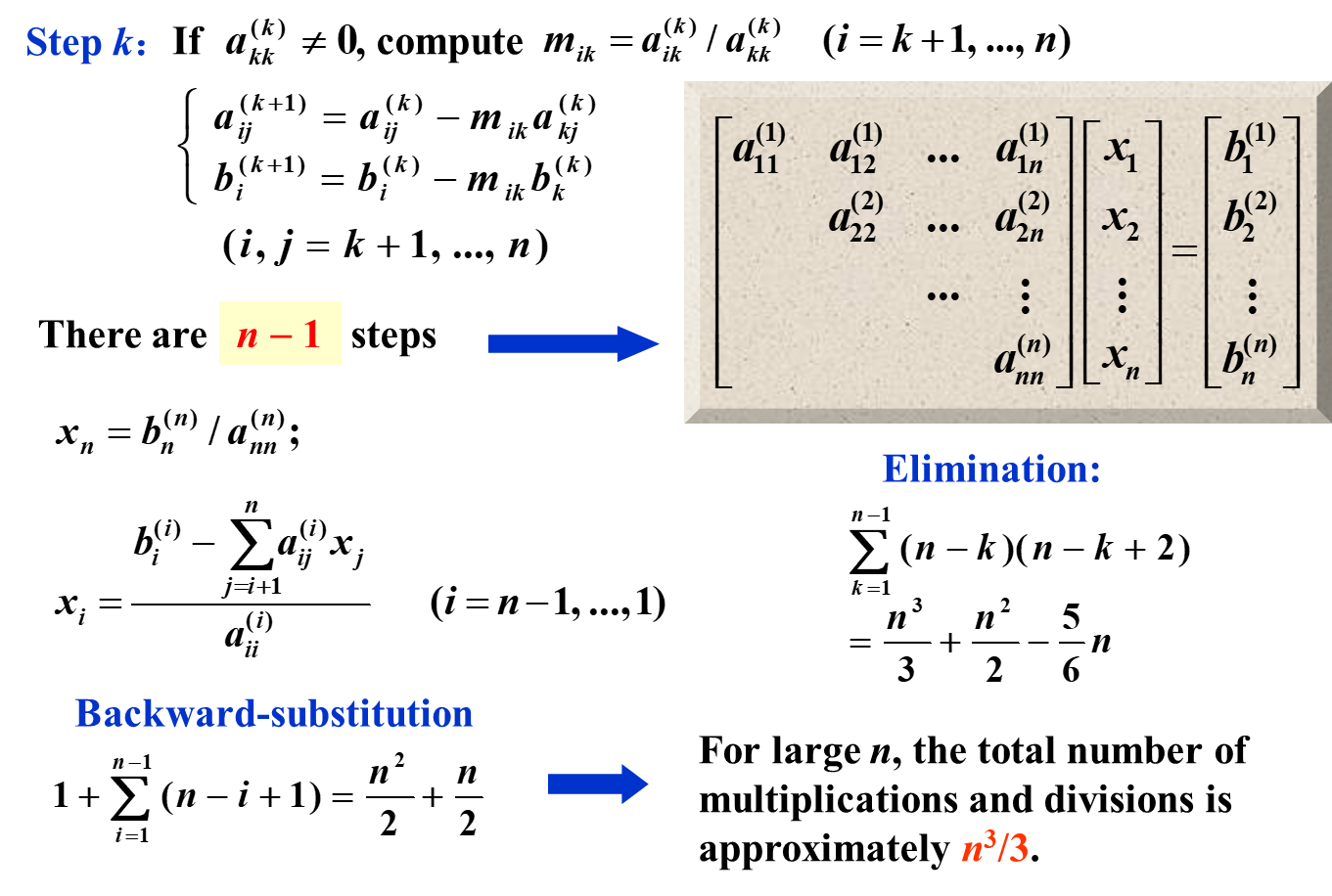
image-20240313162015741

Naive 高斯消元的计算复杂度为 \(n^3\)。