Skip to content

Lec 2: Equations

Bisection

注意两点：

c = a + (b - a) / 2; // Don't use (a + b) / 2, in case of precision loss.

if (sign(b) * sign(a) > 0) // Don't use b * a / 2, in case that a * b == 0

可用于任意连续函数

Fix-point Method

我们希望把方程 \(f(x) = 0\) 转换成 \(x = g(x)\)。

  • 比如：\(x^2 - 5x +1= 0\) 转换成 \(g(x) = f(x) + x = x^2 -4x + 1=x\)

我们从 \(p_0\) 开始，按照上述递推关系，求出一个序列 \(\{p_i\}_{i \in \N}\)，使得：\(p_{i+1} = g(p_i)\)

如果 \(\lim_{i \to \infty} p_i = p^*\)，且 \(g\) 连续，那么：

\[ g(p^*) = g(\lim_{i \to \infty} p_i) = \lim_{i \to \infty} g(p_i) = \lim_{i \to \infty} p_{i+1} = p^* \]

Fix-point Theorem

Theorem 1: 假如

  • \(g \in C[a,b]\) s.t. \(g(x) \in [a,b]\)
    • 保证值域包含于定义域内
  • \(\exists k \in (0,1), \forall x \in (a,b): \lvert g'(x) \rvert \leq k\)
  • \(p_0 \in [a,b]\)
    • 保证数学归纳法的 initial condition is satisfied

那么，上述数列一定收敛

Proof: $$ \frac {\lvert p_{i+2} - p_{i+1} \rvert} {\lvert p_{i+1} - p_{i} \rvert} = \frac {\lvert g(p_{i+1}) - g(p_{i}) \rvert} {\lvert p_{i+1} - p_{i} \rvert} = \lvert g'(\xi) \rvert \leq k $$ 通过数学归纳法，可以容易证明 \(g(p_0) \neq p_0 \implies \{p_i\}_{i \in \mathbb{Z}^+} \in (a,b)\) ，从而就在我们讨论的定义域内。

  • 如果 \(g(p_0) = p_0\)，就没有算的必要了

由于两项之差以至少指数级的速度收敛（以及每一项与真值之差），因此是 Cauchy 列，容易证明收敛。

Corollary 1: $$ | p _ { n } - p | \leq \frac { 1 } { 1 - k } | p _ { n + 1 } - p _ { n } | \text{ and } | p _ { n } - p | \leq \frac { k ^ { n } } { 1 - k } | p _ { 1 } - p _ { 0 } | $$ Proof: 易证

根据推论，我们可以

  • 通过 \(| p_1 - p_0 |\) 来确定最多迭代次数
  • 通过 \(| p _ { n+1 } - p _{n}|\) 来实时判断停止

Newton's Method

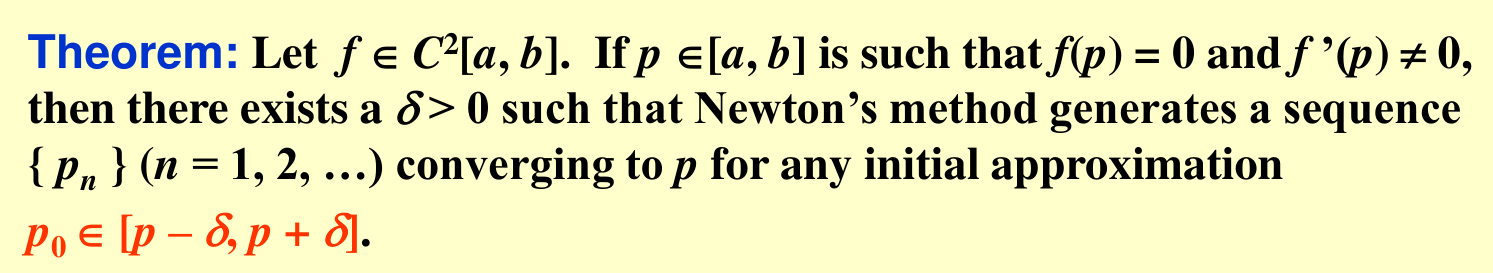
image-20240306115410566

Proof:

令 \(g(x) = x - \frac {f(x)}{f'(x)}\)，然后我们可以去套 fix-point method 的条件。

First condition: \(g \in C[p - \delta, p + \delta]\) s.t. \(g(x) \in [p - \delta, p + \delta]\)

\(|g(x) - p| = |g(x) - g(p)| = |x-p||g'(\xi)| \leq k|x-p| \leq |x-p| \leq \delta\)

  • 需要依靠 second condition 的保证
  • 另外，在 Newton's Method 下，second condition（以及 \(g\) 可导）可以直接推出 first condition
    • 因为，\(a=p-\delta, b=p+\delta\) 是关于 \(p\) 对称的
    • 而一般的不动点定理的条件，并没有这样的条件

Second condition: \(\exists k \in (0,1), \forall x \in (p - \delta, p + \delta): \lvert g'(x) \rvert \leq k\)

\(g'(x) = \frac{f(x)f''(x)}{f'(x)^2}\)，由于二阶导连续，一阶导不等于 0，因此 \(g'(x)\) 连续。

由于 \(f(p) = 0\)，因此 \(g'(p) = 0\)，因此，\(\forall k \in (0,1), \exists \delta > 0, \forall x \in [p - \delta, p + \delta]: |g'(x)| \leq k\)

Third condition: \(p_0 \in [p - \delta, p + \delta]\)

显然。

至于为什么 \(\delta\) 无法精确得到，这是因为我们并不知道 \(g'(x)\) 能够在那个范围内 bound 住。

如果能够推导出 \(g'(x)\) 能够在某个区域中，被某个 \(k \in (0,1)\) bound 住。那么，就能够更加保险地使用这个方法。

多项式求根

多项式求根的精确+高效算法，到现在还是一个 open problem。