Skip to content
\[ \newcommand{op}{\operatorname*} \]

Lec 2: SQL Basics

Basic Structure

Formally, given sets \(D_1, D_2, \dots, D_n\), a relation r is a subset of \(D_1 \times D_2 \times\dots\times D_n\) Thus, a relation is a set of n-tuples \((a_1,a_2,\dots,a_n)\) where each \(a_i \in D_i\)

  • NOTE: Relation is a set, like {(Wu, Finance, 80000), (Liu, Commerce, 60000), (Mozart, Music, 114514), (Musk, Leader, 1919810)}. A set doesn't has a order.

Relation Schema & Instance

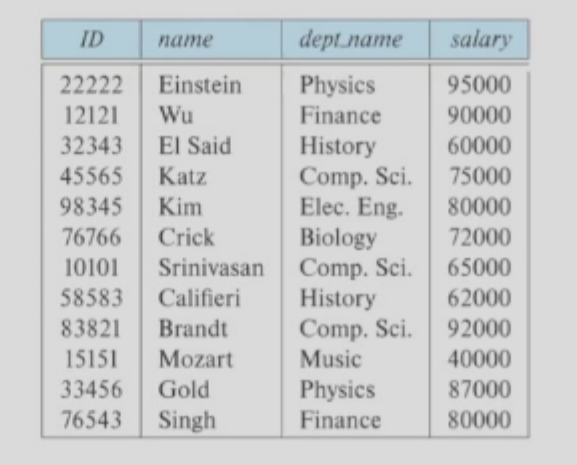
  • \(A_1, A_2, \dots, A_n\) are attributes
    • e.g. ID, name, dept_name, salary
    • It has both name and domain of its values
  • \(R = (A_1, A_2, \dots, A_n)\) is a relation schema
    • e.g. instructor = (ID, name, dept_name, salary)
    • NOTE: Relation is unordered tuple
  • A relation instance r defined over schema R is denoted by r(R).
    • Analogy: if schema is type, instance is value
    • e.g. image-20240307142609901

Attributes

  • The set of allowed values for each attribute is called the domain of the attribute
  • Attribute values are (normally) required to be atomic; that is, indivisible
    • Analogy: atomic value is like basic data types
  • The special value null is a member of every domain
    • used to represent that this value hasn't been initialized
    • The null value causes complications in the definition of many operations

Key

Key is a subset of \(R\).

主键

对于一个关系，可能有多个满足下列条件的属性。我们从中选取一个有代表性的属性，称为主键 (main key) 。主键必须

  • 非空
  • （在一个 instance 内）唯一

外键

我们还可以定义外键。如果让 r1 的外键（记作 \(k_1\)）与 r2 的某个键（记作 \(k_2\)）与 r2相联系，那么，DBMS 就要保证 r1 每一项的\(k_1\)，在 r2 其中一项的 \(k_2\) 中存在。

比如可以这样处理（当然也有别的处理方法）：

  • r1 添加 entry 的时候，其 \(k_1\) 必须在某个 entry 的 \(k_2\) 中存在
  • r2 删除 entry 的时候，其 \(k_2\) 必须在所有 entry 的 \(k_1\) 中不存在

同样，由于主键非空，因此外键也非空。

参照完整性

与外键类似，但是 \(k_2\) 不必是主键。

例子：Schema Diagram for University Database

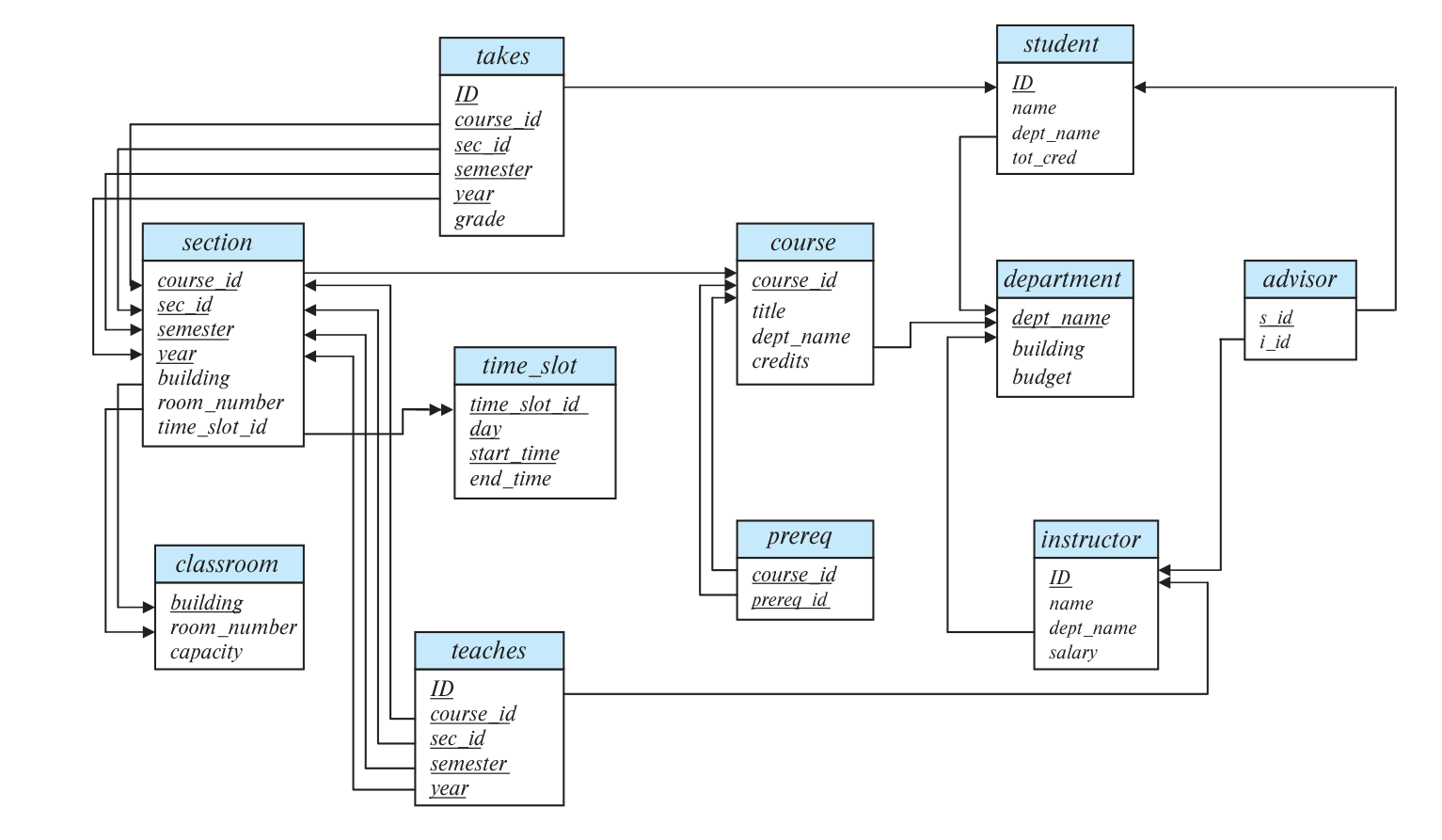
image-20240307150509159

  • 其中，单箭头就是外键，双箭头就是参照完整性约束，下划线就是该 schema 的主键
    • 对于主键，我们的目的是保证唯一
    • 对于外键/参照完整性约束，我们的目的就是保证输入内容合法

RQL (Relational Query Languages)

常见的有：

  • \(\cup, -\): Union, Difference
    • The arity of the attributes of the two sets \(R_1, R_2\) must be the same
    • And the types of each corresponding attribute pair must be compatible
      • i.e. of the same type
    • NOTE: Set intersection can be defined by set difference, i.e. \(r \cap s := r - (r - s) := s - (s - r)\)
  • \(\times\): Cartesian Product
  • \(\newcommand{Proj}{\Pi}\Proj\): Projection
    • \(\Pi_{a_1, \dots, a_n}(R)\), where \(a_1, \dots, a_n\) are attributes
    • To restrict all tuples in \(R\) to the set \(\{a_1, \dots, a_n\}\)
      • NOTE: Some DMBS's are actually multi-set, so you have to use DISTINCT keyword to make the result distinct, since making the DMBS distinct is time-consuming.
  • \(\newcommand{Select}{\sigma}\Select\): Selection
    • \(\sigma_{\varphi}(R)\), where \(\varphi\) is proposition formula
    • To select only those tuples satisfying \(\varphi\)
  • \(\rho\): Rename
    • \(\phi_{a/b}(R)\)
    • To rename \(b\) attributes in all tuples to \(a\) attributes

Example

Q1: Find the names of all instructors in the Physics department, along with the course_id of all courses they have taught

A1: \(\Proj_{i.name, t.course\_id}(\Select_{i.dept\_name=''Physics''}(\Select_{t.id = i.id}(\op{inst} \times \op{teaches})))\)

Q2: Find the names of all instructors in the Physics department, along with the course_id and the title of all courses they have taught

A2: \(\Proj_{i.name, t.course\_id, c.title}(\Select_{i.dept\_name=''Physics'' \land t.id = i.id \land t.course\_id = c.course\_id}(\op{inst} \times \op{teaches} \times \op{courses}))\)

Q3: Find the largest salary in the university

A3: First, find all salaries that are smaller than other salaries. Next, remove those from all the salaries.

image-20240307172320702

Q4: Find all the direct and indirect prerequisites of the course with title "Computer Network"

A4: We are unable to make this query with these basic operations. And also, basic RQL is NOT Turing complete. So there is ought to be infinitely many tasks that it can't handle while an arbitrary TC language can.

NOTE: \(\times\) is often the most time-consuming operation in a query, so there will be many optimizations

  • like first \(\Select_{i.{dept\_name}=''Physics''}\) to reduce the inst table, then \(\Select_{t.id=i.id}\), finally \(\Select_{t.course\_id=c.course\_id}\)

Some aliases

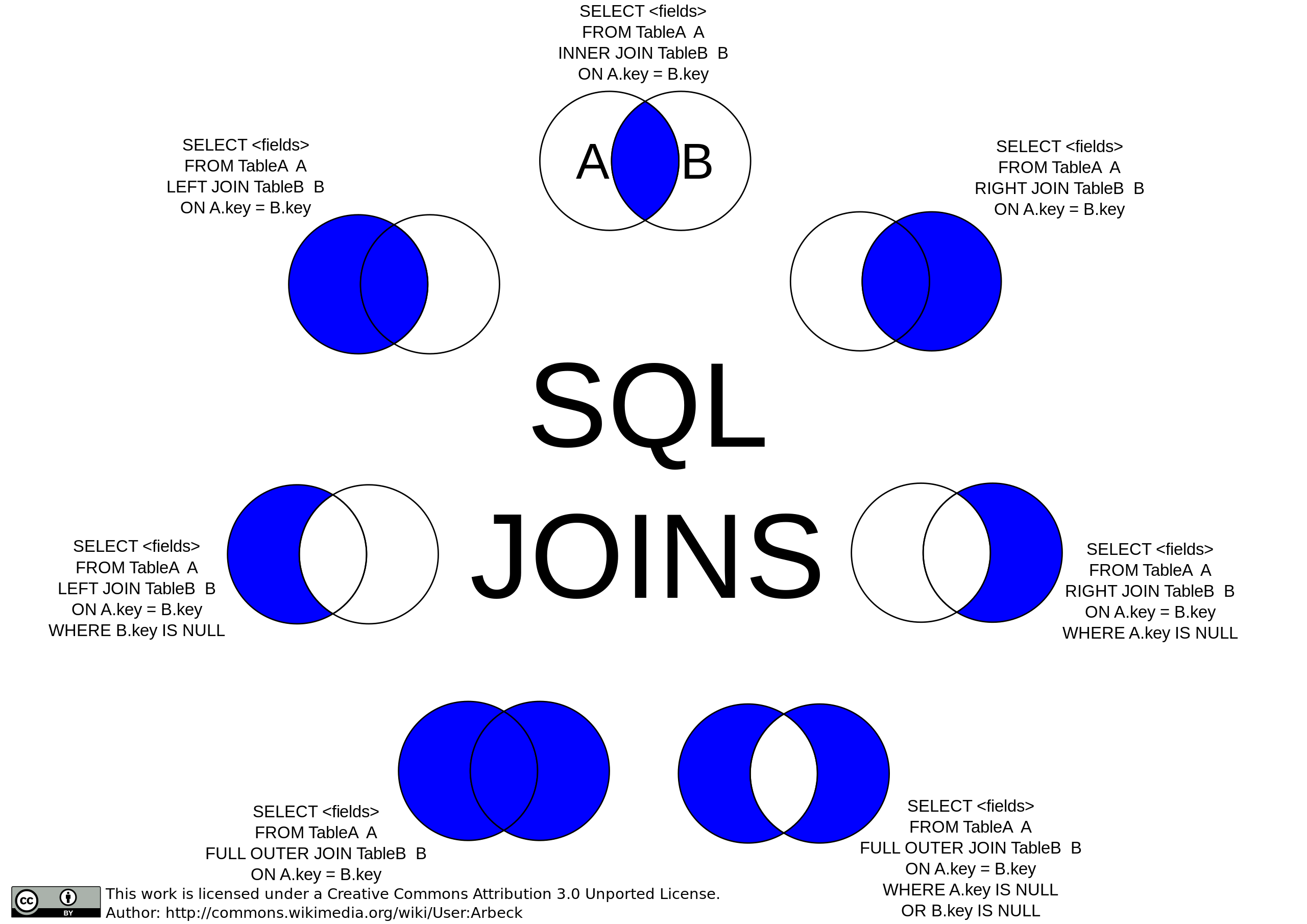
File:SQL Joins.svg - Wikimedia Commons

Set intersection, joins and join-like ops are like the aliases of some complex operations that can be performed solely with the six basic operations:

  • \(\cap\): Set intersection
  • \(\bowtie\): Natural join (or inner join)
    • \(r \bowtie s = \Proj_{(r+s-common)}(\Select_{s.commom = r.common}(r \times s))\)
  • \(⟖, ⟕, ⟗\): Outer join
    • \(r ⟕ s := (r \bowtie s) \cup ((r - \Proj_R(r \bowtie s)) \times \{(\op{null}, \dots, \op{null})\})\)
    • \(r ⟖ s := (r \bowtie s) \cup (\{(\op{null}, \dots, \op{null})\} \times (s - \Proj_S(r \bowtie s)))\)
    • \(r ⟗ s := (r \bowtie s) \cup ((r - \Proj_R(r \bowtie s)) \times \{(\op{null}, \dots, \op{null})\}) \cup (\{(\op{null}, \dots, \op{null})\} \times (s - \Proj_S(r \bowtie s)))\)
  • \(\bowtie_\theta\): Natural join with condition
    • \(r \bowtie_\theta s := \Select_\theta(r \bowtie s)\)
  • \(\ltimes_{\theta}\): Semijoin
    • \(r \rtimes_\theta := \Proj_R(r \bowtie_\theta s)\)
    • \(r \ltimes_\theta := \Proj_S(r \bowtie_\theta s)\)
    • NOTE: Semijoin is NOT among the seven circumstances shown in the image above.
  • \(\leftarrow\): Assignment

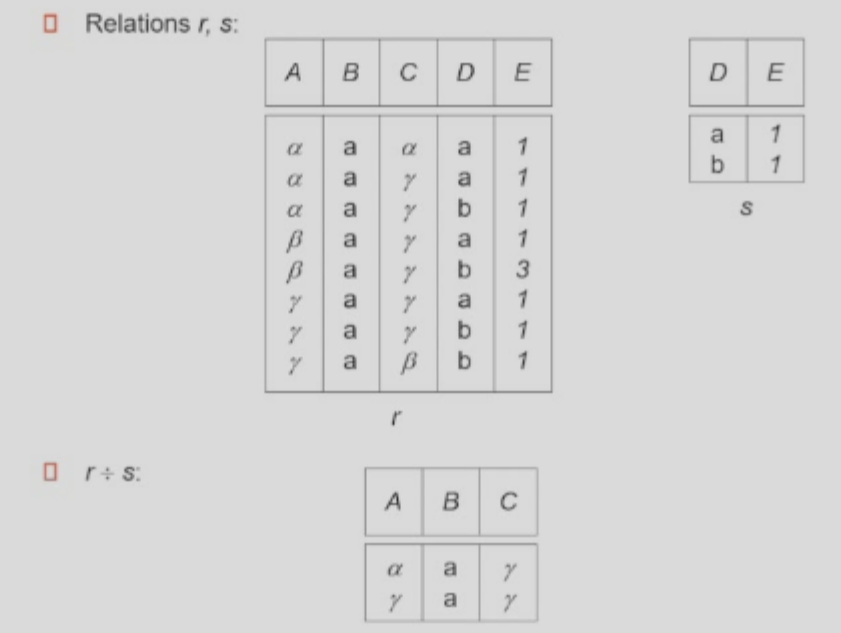
  • \(r \div s\): Division

    • Given relations \(r(R)\) and \(s(S)\), s.t. \(S \subsetneq R\), \(r\div s\) is the largest relation \(t(R - S)\) s.t. \(t \times s \subseteq r\)

    • \[ \begin{aligned} temp1 &\leftarrow \Proj_{R-S}(r), \text{ i.e. all the R-S of (r, s)}\\ temp2 &\leftarrow \Proj_{R-S}(temp1 \times s - \Proj_{R-S, S}(r)), \\ & \quad ~~\text{ i.e. the entries in the R-S of (r, s) that aren't subset of r after joining s} \\ result &= temp1 - temp2 \end{aligned} \]

    • Example: image-20240307183304964

Example

Find all the instructors that have taught at least one course in year 2022. $$ \prod _ { n a m e } ( i n s t r u c t o r \ltimes _ { i n s t r u c t o r . I D = t e a c h e s . I D} ( \sigma _ { t e a c h e s . y e a r = 2 0 2 2} ( t e a c h e s ) ) ) $$

Some extensions

Generalized projections

Instead of pure attributes, the \(F_1, \dots, F_n\) are now arithmetic expressions involving constants and attributes in the schema of \(E\)

  • e.g. \(\Proj_{ID, name, dept\_name, salary / 12}\)

Aggregate Functions and Operations

  • avg: average
  • valuemin: minimum
  • valuemax: maximum
  • valuesum: sum of values
  • count: number of values

image-20240307185549008

This can be translated into SQL code:

SELECT
    G1,G2,...,Gn,
    F1(A1),F2(A2),...,Fn(An)
FROM
    E
GROUP BY
    G1,G2,...,Gn

Note:

SELECT
    G1,G2,...,Gn,
    F1(A1),F2(A2),...,Fn(An)
FROM
    E
GROUP BY
    H1(G1),H2(G2),...,Hn(Gn)

is equivalent to

SELECT
    G1,G2,...,Gn,
    F1(A1),F2(A2),...,Fn(An)
FROM
(
    SELECT
        H1(G1) AS G1,H2(G2) AS G2,...,Hn(Gn) AS Gn
    FROM
        E
) AS E
GROUP BY
    G1,G2,...,Gn

which means it's a mere composition of generalized projection and aggregation.

Example:

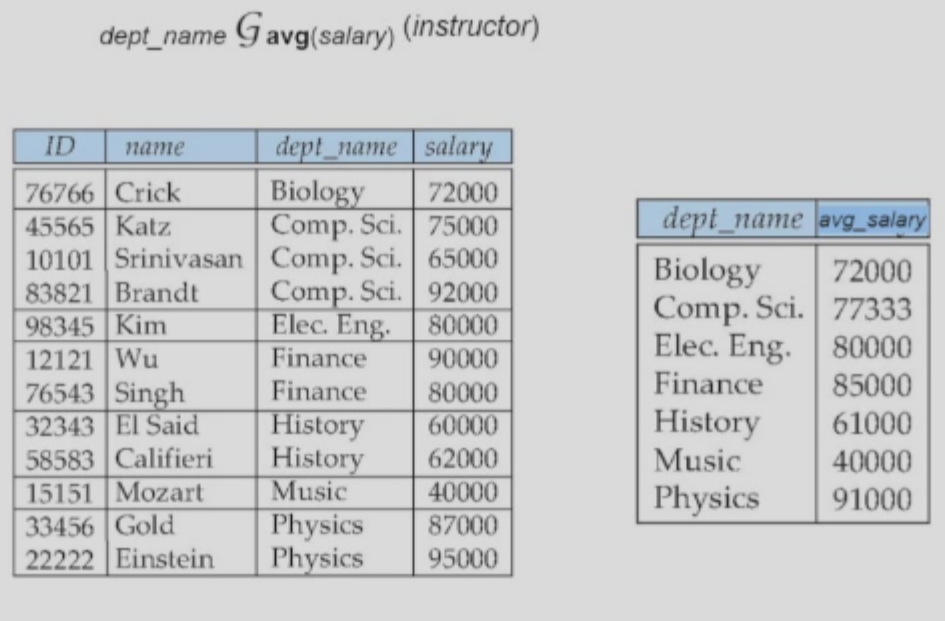
image-20240307191455874

This can be translated into MySQL code:

SELECT
    dept_name,
    AVG(salary)
FROM
    instructor
GROUP BY
    dept_name

Multiset Relational Algebra

背景：由于去重操作在数据库中是一个繁重的工作，因此，我们很多情况下用的是 Multiset Relational Algebra。

如下图，我们可以将 Multiset Relational Algebra 对应到前面讨论的 Set Relational Algebra 之中。

  • 如果一个集合是 \(\op{Set}\)，那么，其对应的 multiset 就是 \(\op{Set} \times \Z^+\)，其中，自然数代表 \(\op{Set}\) 中某一个元素的 number of copies。

image-20240307195900302