四
本文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
在这一部分中,我们将进一步了解线性代数如何高效地帮助我们计算拓扑特性。
来自线性代数的拯救¶
您可能已经注意到,对于比我们目前考虑的简单示例要大得多的东西,手工计算同调群和连通数是非常乏味和不切实际的。幸运的是,有更好的方法。特别是,我们可以用向量和矩阵的语言来进行同调群的大部分计算和表达,而计算机在处理向量和矩阵时是非常高效的。
现在,我们已经讲过向量是什么 (向量空间中的元素),但是什么是矩阵呢?你可能会想到一个矩阵有一个二维的数字网格,你知道你可以将矩阵乘以其他矩阵和向量。对于矩阵来说,一个数字网格当然是一个方便的符号,但这不是矩阵的本质。
什么是矩阵?¶
至此,您应该对函数或映射的概念非常了解了。这两种方法都是将一种数学结构转换成另一种结构 (或者至少将结构中的一个元素映射到同一结构中的不同元素)。特别是,我们花了大量的时间使用边界映射,将一个高维链群映射到一个更低维度的链群,以某种方式保留了原始组的结构 (这是一种同态)。
就像我们可以有两个群之间的映射,也可以有两个向量空间之间的映射。我们称在向量空间之间的 (线性) 映射为矩阵。矩阵基本上是在向量空间 (或单个向量元素) 上应用线性变换产生新的向量空间。线性变换意味着我们只能通过常数和常数向量的加法来变换向量空间。
定义(线性变换):
线性变换 \(M\ :\ V_1 \rightarrow V_2\) 是从 \(V_1\) 到 \(V_2\) 的映射 \(M\) ,例如 \(M(V_1 + V_2) = M(V_1) + M(V_2)\) 和 \(M(aV_1) = aM(V_1)\) ,其中 \(a\) 是标量。
假如我们想将实数体 \(\mathbb R^3\) 映射到平面 \(\mathbb R^2\) 。
\(\begin{aligned} V_1 &= span\{(1,0,0),(0,1,0),(0,0,1)\} \\ V_2 &= span\{(1,0),(0,1)\} \end{aligned}\)
现在,如果想从 \(V_1\) 映射到 \(V_2\) ,就是说,我想将 \(V_1\) 的每一个点对应到 \(V_2\) 的点。我想做这样的事情有很多原因。例如,如果我要做一个图形应用程序,我想提供一个选项来旋转所绘制的图像,而这仅仅是一个在像素上应用线性变换的问题。
所以我们称映射 \(M\ :\ V_1 \rightarrow V_2\) 叫矩阵。注意到 \(V_1\) 有三个元素,而 \(V_2\) 有两个元素。为了从一个空间映射到另一个空间,我们只需要将一个基集映射到另一个基集。记住,因为这是一个线性映射,我们所能做的就是把它乘以一个标量,或者加上另一个向量,我们不能做奇异的变化,如平方项或者取对数。
我们称三个基础要素为 \(V_1: B_1, B_2, B_3\) 。所以, \(V_1 = \langle{B_1, B_2, B_3}\rangle\) 。同理,我们称两个基本要素为 \(V_2: \beta_1, \beta_2\) 。所以, \(V_2 = \langle{\beta_1, \beta_2}\rangle\) 。(尖括号代表张成,即这些元素的所有线性组合集合)。我们可以利用每个向量空间都可以由它们的基来定义的事实来设置方程,使得 \(V_1\) 中的向量可以映射到 \(V_2\) 。
新符号(向量)
为了防止标量符号和矢量的符号之间的混淆,我将在每个向量上加一个小箭头 \(\vec{v}\) 表示它是一个向量,而不是一个标量。记住,标量只是来自定义向量空间的基础域 \(F\) 的一个元素。
我们可以用下列方法定义映射 \(M(V_1) = V_2\) :
\(\begin{aligned} M(B_1) &= a\vec \beta_1 + b\vec \beta_2 \mid a,b \in \mathbb R \\ M(B_2) &= c\vec \beta_1 + d\vec \beta_2 \mid c,d \in \mathbb R \\ M(B_3) &= e\vec \beta_1 + f\vec \beta_2 \mid e,f \in \mathbb R \\ \end{aligned}\)
也就是说, \(V_1\) 的每个基的映射是由 \(V_2\) 的基线性组合组成的。这需要我们定义总共 6 个新数据: \(a,b,c,d,e,f \in \mathbb R\) 被用作映射。我们只需要注意 \(a,b\) 映射到 \(\beta_1\) 和 \(d,e,f\) 映射到 \(\beta_2\) 。怎样才能最方便的跟踪记录所有这些工作呢?是矩阵。
\(M = \begin{pmatrix} a & c & e \\ b & d & f \\ \end{pmatrix}\)
这是一种非常方便的表达映射 \(M\ :\ V_1 \rightarrow V_2\) 的方法。注意到矩阵的每一列都对应每个 \(M(B_n)\) 的 “映射方程” 的系数。同时也要注意到这个矩阵的维数, \(2\times3\) 对应我们要映射的两个向量空间的维数。也就是说,任何映射 \(\mathbb R^n \rightarrow \mathbb R^m\) 都能被表示为一个 \(m\times n\) 矩阵。重要的是要记住,由于线性映射 (以及因此矩阵) 依赖于一个基的系数,那么如果一个人使用不同的基底,那么矩阵元素就会改变。
知道这一点,我们可以很容易地看出向量矩阵乘法是如何工作的,以及为什么矩阵和向量的维数必须一致。也就是说, \(n\times m\) 的向量 / 矩阵乘以 \(j\times k\) 的向量 / 矩阵要得到 \(n\times k\) 的向量 / 矩阵,前提是使等式有效,必须 \(m=j\) 。
这就是我们拿矩阵映射 \(M\) 乘以向量 \(V_1\) ,得到向量 \(V_2\) 的方法:
\(M(\vec v\ \in\ V_1) = \underbrace{ \begin{bmatrix} a & c & e \\ b & d & f \\ \end{bmatrix}}_{M:V_1\rightarrow V_2} \underbrace{ \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix}}_{\vec v\ \in\ V_1} = \underbrace{ \begin{bmatrix} a * x & c * y & e * z \\ b * x & d * y & f * z \\ \end{bmatrix}}_{M:V_1\rightarrow V_2} = \begin{pmatrix} a * x + c * y + e * z \\ b * x + d * y + f * z \\ \end{pmatrix} \in V_2\)
现在我们知道一个矩阵是两个向量空间之间的线性映射。但是如果把两个矩阵相乘会怎样呢?这只是映射的组成部分。例如,我们有三个向量空间 \(T, U, V\) 和两个线性映射 \(m_1,m_2\) :
\(\\T \stackrel{m_1}{\rightarrow} U \stackrel{m_2}{\rightarrow} V\)
为了从 \(T\) 到 \(V\) ,我们需要运用两次映射 \(m_2(m_1(T)) = V\) 。因此,把两个矩阵相乘给了我们映射的组合 \(m_2 \circ m_1\) 。单位矩阵,即在除了对角线是 \(1\) ,所有其他地方是 \(0\) 的形式,是一个恒等映射(即不会改变输入值),例如:
⋰⋰
\(\\ m \vec v = \vec v, \forall \vec v \in V\)¶
(再次)回到单纯同调¶
我们已经过了一遍以上矩阵的必须内容作为铺垫,那我们现在能将边界映射 \(\partial(C_n)\) 表达成矩阵的形式,这样我们才能使用线性代数的工具。这很容易理解,因为我们已经知道当我们允许标量相乘时,链群 \(C_n\) 就能看作向量空间,那么在链向量空间之间的线性映射就是边界图,我们可以表示为一个矩阵。
我们表示一个 \(n\) 维边界映射,即 \(\partial(C_n)\) ,为一个 \(k\) 列, \(l\) 行的矩阵,其中 \(n\) 是链群的维度, \(k\) 是 \(C_n\) 中单形的数量,而 \(l\) 是 \(C_{n-1}\) 中单形的数量。因此每一列代表 \(C_n\) 的单形,每一行代表 \(C_{n-1}\) 的单形。如果这个列的单形映射到这一行的单形,我们就让矩阵的这一格为 \(1\) 。例如,如果域是 \(\mathbb Z\) ,则 \(\partial([a,b]) = a - b\) ,那我们 \(a\) 列和 \(b\) 列等于 \(1\) ,因为 \(1\) 维单形 \([a,b]\) 映射到两个 \(0\) 维单形中。
让我们用矩阵和向量来计算前面的单纯复形的同调群。我们将倒回去用 \(\mathbb Z_2\) 作为我们的域(所以单形的方向可以忽略),因为这样做的计算效率更高。
\(\\S = \text{ {[a], [b], [c], [d], [a, b], [b, c], [c, a], [c, d], [d, b], [a, b, c]} }\)
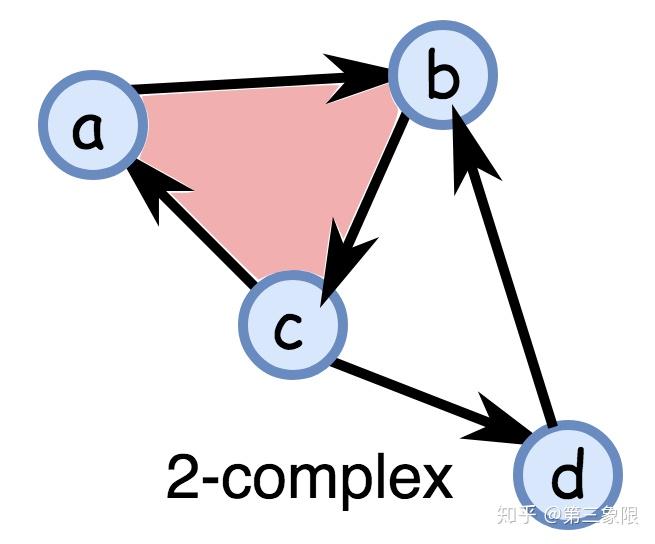
因为我们用的是(非常小)有限域 \(\mathbb Z\) , 然后我们可以列出链 (群) 向量空间中的所有向量。我们有 \(3\) 个链群,即 \(0\) 维单形(顶点), \(1\) 维单形(边界), \(2\) 维单形(三角形)的群。
在我们的例子中,我们只有一个 \(2\) 维单形: \([a,b,c]\) ,因此它在域 \(\mathbb Z_2\) 上生成的群是 \(\{0, [a,b,c]\}\) ,这与 \(\mathbb Z_2\) 同构。一般来说,由单纯复形中 p 维单形的数量 \(n\) 组成的群与 \(\mathbb Z^n_2\) 同构。为了让电脑理解,我们可以用它们的系数 \(0\) 或 \(1\) 来对群元素进行编码。所以,例如,由 \([a,b,c]\) 生成的群只需要用 \(\{0,1\}\) 就能表示。或者 \(0\) 维单形 \(\{a, b, c, d\}\) 生成的群能用 \(4\) 维向量表示,如,如果群的元素是 \(a+b+c\) ,那么我们用 \((1,1,1,0)\) 编码,其中每个位置分别表示 \((a,b,c,d)\) 存在与否。
这里所有的链群都表示为带系数的向量(我没有把 \(C_1\) 所有元素都列出来,因为这太多了 [32]):
\(\begin{align} C_0 &= \left\{ \begin{array}{ll} (0,0,0,0) & (1,0,0,0) & (0,1,1,0) & (0,1,0,1) \\ (0,1,0,0) & (0,0,1,0) & (0,0,1,1) & (0,1,1,1) \\ (0,0,0,1) & (1,1,0,0) & (1,0,0,1) & (1,0,1,1) \\ (1,1,1,0) & (1,1,1,1) & (1,0,1,0) & (1,1,0,1) \\ \end{array} \right. & \cong \mathbb Z^4_2 \\ C_1 &= \left\{ \begin{array}{ll} (0,0,0,0,0) & (1,0,0,0,0) & (0,1,1,0,0) & (0,1,0,1,0) \\ (0,1,0,0,0) & (0,0,1,0,0) & (0,0,1,1,0) & (0,1,1,1,0) \\ \dots \end{array} \right. & \cong \mathbb Z^5_2 \\ C_2 &= \left\{ \begin{array}{ll} 0 & 1 \end{array} \right. & \cong \mathbb Z_2 \end{align}\)
为了把 \(p\) 维单形的群的边界映射 (即线性映射) 表示为一个矩阵,我们用列表示群中的每一个 \(p\) 维单形,并用行表示每个 \((p-1)\) 维单形。我们让矩阵的每个位置等于 \(1\) ,如果 \((p-1)\) 维单形行是 \(p\) 维单形列的面。
我们用有序对 \((i,j)\) 分别指代行和列。那么元素 \(a_{2,3}\) 代表第 \(2\) 行(从上开始)第 \(3\) 列(从左开始)的元素。
因此,一般的边界矩阵(每列是 \(p\) 维单形,每行是 \((p-1)\) 维单形)是这样的:
\(\\\begin{align} \partial_p &= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,j} \\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,j} \\ a_{3,1} & a_{3,2} & a_{3,3} & \cdots & a_{3,j} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{i,1} & a_{i,2} & a_{i,3} & \cdots & a_{i,j} \end{pmatrix} \end{align}\)
我们将从把边界映射 \(\partial(C_2)\) 表示成矩阵开始。 \(C_2\) 中只有一个 \(2\) 维单形,所以矩阵只有一列,但 \(C_1\) 有五个 \(1\) 维单形,所以有五行。
\(\\\partial_2 = \begin{array}{c|lcr} \partial & [a,b,c] \\ \hline [a,b] & 1 \\ [b,c] & 1 \\ [c,a] & 1 \\ [c,d] & 0 \\ [d,b] & 0 \\ \end{array}\)
如果行元素是单形 \([a,b,c]\) 的面,我们就让它等于 \(1\) 。这个矩阵是有意义的线性映射因为如果我们把它乘以一个 \(C_2\) 的向量元素(除了 \(0\) 元素外,只有 \(1\) 元素),我们得到了我们所期望的:
\(\\\begin{align} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} * 0 \qquad &= \qquad \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix} \\ \begin{pmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} * 1 \qquad &= \qquad \begin{pmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} \end{align}\)
好的,让我们继续构建边界矩阵 \(\partial(C_1)\) :
\(\\\partial_1 = \begin{array}{c|lcr} \partial & [a,b] & [b,c] & [c,a] & [c,d] & [d,b] \\ \hline a & 1 & 0 & 1 & 0 & 0 \\ b & 1 & 1 & 0 & 0 & 1 \\ c & 0 & 1 & 1 & 1 & 0 \\ d & 0 & 0 & 0 & 1 & 1 \\ \end{array}\)
这有意义吗?让我们用 python/numpy 检查一下。让我们从 \(1\) 维链的群中取一个任意的元素,即 \([a,b]+[c,a]+[c,d]\) ,我们把它编码成 \((1,0,1,1,0)\) 并应用边界矩阵,看看我们能得到什么。
import numpy as np
b1 = np.matrix([[1,0,1,0,0],[1,1,0,0,1],[0,1,1,1,0],[0,0,0,1,1]]) #boundary matrix C_1
el = np.matrix([1,0,1,1,0]) #random element from C_1
np.fmod(b1 * el.T, 2) # we want integers modulo 2
将 \((0,1,0,1)\) 转换成 \(b+d\) ,我们可以手工计算并比较边界:
\(\\\partial([a,b]+[c,a]+[c,d]) = a+b+c+a+c+d = \cancel{a}+b+\cancel{c}+\cancel{a}+\cancel{c}+d = b+d = (0,1,0,1)\)
这行得通!
最后,我们需要 \(C_0\) 的边界矩阵,这很简单,因为 \(0\) 维单形的边界总是映射到 \(0\) ,所以:
\(\\\partial_0 = \begin{pmatrix} 0 & 0 & 0 & 0 \\ \end{pmatrix}\)
是 OK 的,现在我们有了三个边界矩阵,我们怎么计算连通数呢?回想一下链群的子群序列: \(B_n \leq Z_n \leq C_n\) ,它们分别是边界群,循环群和链群。
再重温一下连通数的定义: \(b_n = dim(Z_n\ /\ B_n)\) 。但这是用群结构表示的集合,现在所有东西都被表示成向量和矩阵,所以我们重新定义了连通数 \(b_n = rank(Z_n)\ -\ rank(B_n)\) 。”rank“ 是什么鬼东西?秩(rank)和维度差不多,但又不一样。如果我们把矩阵的列看成一组基向量: \(\beta_1, \beta_2, \dots \beta_k\) ,那么这些列向量 \(\langle \beta_1, \beta_2, \dots \beta_k \rangle\) 张成的空间的维数就是矩阵的秩。结果是,你也可以使用行,它也会有相同的结果。但是,重要的是,维度是在最小的基元集合上定义的,即线性无关的基元。
矩阵的边界 \(\partial_n\) 包含链群和循环子群的信息,以及 \(B_{n-1}\) 边界子群,我们需要计算的连通数的所有信息。不幸的是,总的来说,我们构建边界矩阵的朴素方法并不是一种可以轻易得到的分群和子群信息的形式。我们需要修改边界矩阵,而不干扰它包含的映射信息,从而形成一种名为 Smith 标准型的新形式。基本上,矩阵的 Smith 标准型是沿着对角线从左上方开始全是 1,而其他地方全是 \(0\) 的形式。例如,
\(\\\begin{align} \text{Smith normal form} &:\ \begin{pmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & ? \end{pmatrix} \end{align}\)
注意到 \(1\) 沿对角线不一定要一直延伸到右下方。而这才是在 Smith 标准型中可用的信息 (红色对角线表示 \(1\) ):
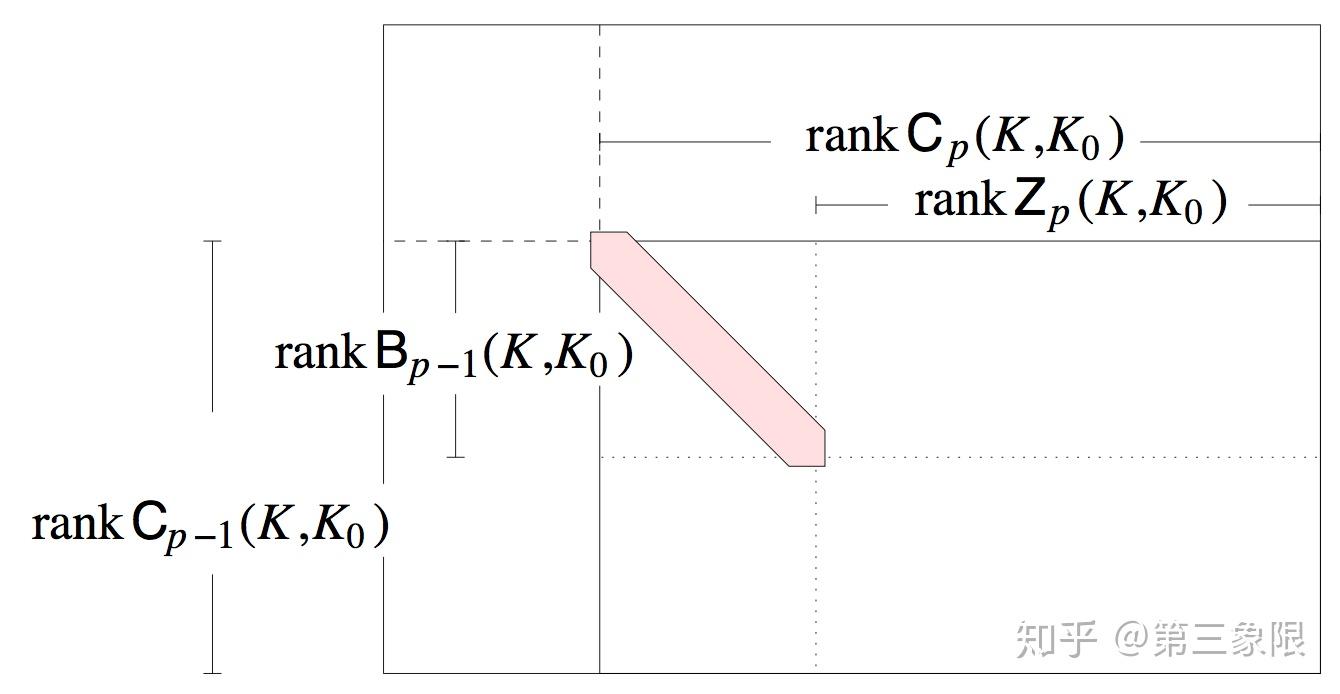
(来源: "COMPUTATIONAL TOPOLOGY" by Edelsbrunner and Harer, pg. 104)
那么怎样才能得到一个 Smith 标准型呢? 我们可以根据规则进行一些操作,以下是矩阵中允许的两个操作:
-
你可以在矩阵中交换任意两列或任意两行。
-
您可以向另一个列添加一个列,或者将一行添加到另一行。
现在你只需要应用这些运算,直到你得到 Smith 标准型的矩阵。我要指出的是,当我们用域 \(\mathbb Z_2\) 时,这个过程并不容易。让我们用边界矩阵 \(C_1\) 试一下。
\(\\\partial_1 = \begin{array}{c|lcr} \partial & [a,b] & [b,c] & [c,a] & [c,d] & [d,b] \\ \hline a & 1 & 0 & 1 & 0 & 0 \\ b & 1 & 1 & 0 & 0 & 1 \\ c & 0 & 1 & 1 & 1 & 0 \\ d & 0 & 0 & 0 & 1 & 1 \\ \end{array}\)
我们已经在对角线上有 \(1\) 了,但是我们有很多 \(1\) 不在对角线上。
步骤:把第 \(3\) 列加到第 \(5\) 列上,再把第 \(4\) 列加到第 \(5\) 列上,然后把第 \(1\) 列加到第 \(5\) 列上:
\(\\\partial_1 = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix}\)
步骤:把第 \(1\) 列和第 \(2\) 列加到第 \(3\) 列上,把第 1 行加到第 \(2\) 行上,把第 \(2\) 行加到第 \(3\) 行上,把第 \(3\) 行加到第 \(4\) 行上,第 \(3\) 列和第 \(4\) 列交换,最后矩阵如下:
\(\\\text{Smith normal form: } \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix}\)
一旦我们有了 Smith 标准型的矩阵,我们就不再做任何运算了,当然,我们可以继续把行和列相加直到我们得到 0 的矩阵,但这并不是很有帮助!我随机添加了行 / 列,让它变成 Smith 标准型,但实际上有一种算法可以相对高效地完成它。
我将使用一个现有的算法,而不是详细地实现 Smith 标准型的算法。
def reduce_matrix(matrix):
#Returns [reduced_matrix, rank, nullity]
if np.size(matrix)==0:
return [matrix,0,0]
m=matrix.shape[0]
n=matrix.shape[1]
def _reduce(x):
#We recurse through the diagonal entries.
#We move a 1 to the diagonal entry, then
#knock out any other 1s in the same col/row.
#The rank is the number of nonzero pivots,
#so when we run out of nonzero diagonal entries, we will
#know the rank.
nonzero=False
#Searching for a nonzero entry then moving it to the diagonal.
for i in range(x,m):
for j in range(x,n):
if matrix[i,j]==1:
matrix[[x,i],:]=matrix[[i,x],:]
matrix[:,[x,j]]=matrix[:,[j,x]]
nonzero=True
break
if nonzero:
break
#Knocking out other nonzero entries.
if nonzero:
for i in range(x+1,m):
if matrix[i,x]==1:
matrix[i,:] = np.logical_xor(matrix[x,:], matrix[i,:])
for i in range(x+1,n):
if matrix[x,i]==1:
matrix[:,i] = np.logical_xor(matrix[:,x], matrix[:,i])
#Proceeding to next diagonal entry.
return _reduce(x+1)
else:
#Run out of nonzero entries so done.
return x
rank=_reduce(0)
return [matrix, rank, n-rank]
## Source: < https://triangleinequality.wordpress.com/2014/01/23/computing-homology/
正如你所见,我们得到了同样的结果,但是这个算法肯定更有效率。
因为每个边界映射给我们 \(Z_n\) (循环)和 \(B_{n-1}\) ( \((n-1)\) 维链群的边界),为了计算链群 \(n\) 的连通数,我们需要 \(\partial_n\) 和 \(\partial_{n+1}\) 。记住,我们现在用 \(b_n = rank(Z_n)\ -\ rank(B_n)\) 来计算连通数。
##Initialize boundary matrices
boundaryMap0 = np.matrix([[0,0,0,0]])
boundaryMap1 = np.matrix([[1,0,1,0,0],[1,1,0,0,1],[0,1,1,1,0],[0,0,0,1,1]])
boundaryMap2 = np.matrix([[1,1,1,0,0]])
##Smith normal forms of the boundary matrices
smithBM0 = reduce_matrix(boundaryMap0)
smithBM1 = reduce_matrix(boundaryMap1)
smithBM2 = reduce_matrix(boundaryMap2)
##Calculate Betti numbers
betti0 = (smithBM0[2] - smithBM1[1])
betti1 = (smithBM1[2] - smithBM2[1])
betti2 = 0 #There is no n+1 chain group, so the Betti is 0
print(smithBM0)
print(smithBM1)
print(smithBM2)
print("Betti #0: %s \n Betti #1: %s \n Betti #2: %s" % (betti0, betti1, betti2))
[matrix([[0, 0, 0, 0]]), 0, 4]
[matrix([[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0]]), 3, 2]
[matrix([[1, 0, 0, 0, 0]]), 1, 4]
Betti #0: 1
Betti #1: 1
Betti #2: 0
很好,这行得通。
但我们跳过了一个重要的步骤。我们首先手动设计了边界矩阵,为了算法化整个过程,从构建单纯复形的数据到计算连通数,我们需要一个算法来用简单复形建立边界矩阵。现在让我们来解决它。
##return the n-simplices in a complex
def nSimplices(n, complex):
nchain = []
for simplex in complex:
if len(simplex) == (n+1):
nchain.append(simplex)
if (nchain == []): nchain = [0]
return nchain
##check if simplex is a face of another simplex
def checkFace(face, simplex):
if simplex == 0:
return 1
elif set(face) < set(simplex): #if face is a subset of simplex
return 1
else:
return 0
##build boundary matrix for dimension n ---> (n-1) = p
def boundaryMatrix(nchain, pchain):
bmatrix = np.zeros((len(nchain),len(pchain)))
i = 0
for nSimplex in nchain:
j = 0
for pSimplex in pchain:
bmatrix[i, j] = checkFace(pSimplex, nSimplex)
j += 1
i += 1
return bmatrix.T
这些是非常简单的辅助函数,用来构建边界矩阵然后使用之前描述的简化算法把它变成 Smith 标准型。别忘了,我们使用的简单复形的例子是这样的:
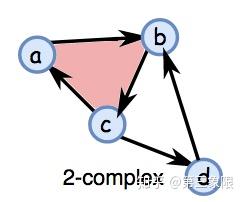
我准备用 \(\{1,2,3,4\}\) 代替 \(\{a,b,c,d\}\) ,这样 python 才能理解它。
S = [{0}, {1}, {2}, {3}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2}] #this is our simplex from above
chain2 = nSimplices(1, S)
chain1 = nSimplices(0, S)
reduce_matrix(boundaryMatrix(chain2, chain1))
[array([[ 1., 0., 0., 0., 0.],
[ 0., 1., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.]]), 3, 2]
现在让我们把所有的东西放在一起,做成一个函数,它会返回单纯复形的所有连通数。
def betti(complex):
max_dim = len(max(complex, key=len)) #get the maximum dimension of the simplicial complex, 2 in our example
betti_array = np.zeros(max_dim) #setup array to store n-th dimensional Betti numbers
z_n = np.zeros(max_dim) #number of cycles (from cycle group)
b_n = np.zeros(max_dim) #b_(n-1) boundary group
for i in range(max_dim): #loop through each dimension starting from maximum to generate boundary maps
bm = 0 #setup n-th boundary matrix
chain2 = nSimplices(i, complex) #n-th chain group
if i==0: #there is no n+1 boundary matrix in this case
bm = 0
z_n[i] = len(chain2)
b_n[i] = 0
else:
chain1 = nSimplices(i-1, complex) #(n-1)th chain group
bm = reduce_matrix(boundaryMatrix(chain2, chain1))
z_n[i] = bm[2]
b_n[i] = bm[1] #b_(n-1)
for i in range(max_dim): #Calculate betti number: Z_n - B_n
if (i+1) < max_dim:
betti_array[i] = z_n[i] - b_n[i+1]
else:
betti_array[i] = z_n[i] - 0 #if there are no higher simplices, the boundary group of this chain is 0
return betti_array
好的,现在我们应该有计算任意以正确格式输入的单纯复形的连通数的集合需要的所有东西。请记住,所有这些代码都是为了学习目的而码的,所以我故意保持了它的简单性。它还不够完整。它基本上没有纠错功能,所以如果它得到了一些出乎意料的东西,它就会崩溃。
但是还是让我们的程序在各种简单复形上运行嘚瑟一下。
\(\\H = \text{ { {0}, {1}, {2}, {3}, {4}, {5}, {4, 5}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2} } }\)
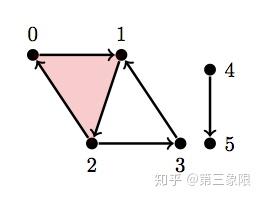
你可以看出这是我们之前一直在用的简单复形,除了现在它在右边有一个断开的边。因此,对于维度 \(0\) ,我们应该得到连通数为 \(2\) ,因为有 \(2\) 个连接组件。
H = [{0}, {1}, {2}, {3}, {4}, {5}, {4, 5}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2}]
betti(H)
我们再试试另一个,这个有 \(2\) 个周期和 \(2\) 个连接的组件。
\(\\Y_1 = \text{ { {0}, {1}, {2}, {3}, {4}, {5}, {6}, {0, 6}, {2, 6}, {4, 5}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2} } }\)
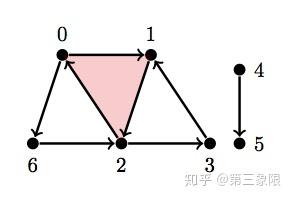
Y1 = [{0}, {1}, {2}, {3}, {4}, {5}, {6}, {0, 6}, {2, 6}, {4, 5}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2}]
betti(Y1)
再来一个。我只是添加了一个顶点:
\(\\Y_2 = \text{ { {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}, {0, 6}, {2, 6}, {4, 5}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2} } }\)
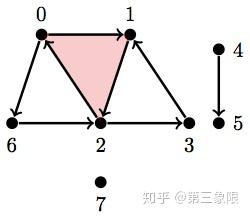
Y2 = [{0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}, {0, 6}, {2, 6}, {4, 5}, {0, 1}, {1, 2}, {2, 0}, {2, 3}, {3, 1}, {0, 1, 2}]
betti(Y2)
最后一个。这是一个空心四面体:
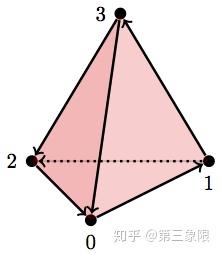
D = [{0}, {1}, {2}, {3}, {0,1}, {1,3}, {3,2}, {2,0}, {2,1}, {0,3}, {0,1,3}, {0,1,2}, {2,0,3}, {1,2,3}]
betti(D)
果然如我们所愿!好的,看起来我们可以可靠地计算任意的单纯复形的连通数了。
预告¶
前 4 篇文章都只是阐述了持续同调背后的数学思想和概念,但到目前为止,我们所做的只是(非持续性的)同调。还记得在第 2 部分中,我们编写了一个为数据构建简单复形的算法吗?回想一下,我们需要任意选择一个参数 \(\epsilon\) ,它决定了两个顶点是否足够近,以将它们连接起来。如果我们选择较小的 \(\epsilon\) ,那么我们会得到一个较为稀疏的图,如果我们选择较大的 \(\epsilon\) ,那么我们会得到一个拥有许多边的稠密的图。
问题是我们无法知道 "正确" 的 \(\epsilon\) 值应该是多少。根据不同的 \(\epsilon\) 值,我们将会得到不同单纯复形(因此有不同的同调群和连通数)。持续同调基本上是说:让我们从 \(0\) 到最大值 (所有顶点都是边缘连接) 不断的扩大 \(\epsilon\) 值 ,并观察哪些拓扑特性持续时间最长。我们相信那些持续时间短的拓扑特征是噪音,而持续时间长的是数据真正的特征。所以下次我们将继续修改算法,在追踪计算的同调群的变化时,能不断变化 \(\epsilon\) 。
参考文献(网站)¶
参考文献(学术刊物)¶
-
Basher, M. (2012). On the Folding of Finite Topological Space. International Mathematical Forum, 7(15), 745–752. Retrieved from http://www.m-hikari.com/imf/imf-2012/13-16-2012/basherIMF13-16-2012.pdf
-
Day, M. (2012). Notes on Cayley Graphs for Math 5123 Cayley graphs, 1–6.
-
Doktorova, M. (2012). CONSTRUCTING SIMPLICIAL COMPLEXES OVER by, (June).
-
Edelsbrunner, H. (2006). IV.1 Homology. Computational Topology, 81–87. Retrieved from http://www.cs.duke.edu/courses/fall06/cps296.1/
-
Erickson, J. (1908). Homology. Computational Topology, 1–11.
-
Evan Chen. (2016). An Infinitely Large Napkin.
-
Grigor’yan, A., Muranov, Y. V., & Yau, S. T. (2014). Graphs associated with simplicial complexes. Homology, Homotopy and Applications, 16(1), 295–311. HHA 16 (2014) No. 1 Article 16
-
Kaczynski, T., Mischaikow, K., & Mrozek, M. (2003). Computing homology. Homology, Homotopy and Applications, 5(2), 233–256. HHA 5 (2003) No. 2 Article 8
-
Kerber, M. (2016). Persistent Homology – State of the art and challenges 1 Motivation for multi-scale topology. Internat. Math. Nachrichten Nr, 231(231), 15–33.
-
Khoury, M. (n.d.). Lecture 6 : Introduction to Simplicial Homology Topics in Computational Topology : An Algorithmic View, 1–6.
-
Kraft, R. (2016). Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology.
-
Lakshmivarahan, S., & Sivakumar, L. (2016). Cayley Graphs, (1), 1–9.
-
Liu, X., Xie, Z., & Yi, D. (2012). A fast algorithm for constructing topological structure in large data. Homology, Homotopy and Applications, 14(1), 221–238. HHA 14 (2012) No. 1 Article 11
-
Naik, V. (2006). Group theory : a first journey, 1–21.
-
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. (2015). A roadmap for the computation of persistent homology. Preprint ArXiv, (June), 17. Retrieved from [1506.08903] A roadmap for the computation of persistent homology
-
Semester, A. (2017). § 4 . Simplicial Complexes and Simplicial Homology, 1–13.
-
Singh, G. (2007). Algorithms for Topological Analysis of Data, (November).
-
Zomorodian, A. (2009). Computational Topology Notes. Advances in Discrete and Computational Geometry, 2, 109–143. Retrieved from CiteSeerX - Computational Topology
-
Zomorodian, A. (2010). Fast construction of the Vietoris-Rips complex. Computers and Graphics (Pergamon), 34(3), 263–271. Redirecting
-
Symmetry and Group Theory 1. (2016), 1–18. Redirecting