二
本文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
单纯形,单纯复形和 VR 复形¶
接下来我们开始写代码。一般来说,我的文章都会涉及到代码,而且非常实用,但是拓扑数据分析并不简单,一个人必须理解基础的数学才能取得进展。
我们将学习如何从 \(\mathbb R^2\) 中一个圆形的模拟数据中构建一个 VR 复形。
我们从这个形状中随机取样,假设它是我们的原始点云数据。许多真正的数据是由循环过程产生的,所以这只是一次不现实的练习。我们将使用我们的点云数据依照上面的描述构建一个 VR 复形。然后我们要用更多的数学方法来确定复形的同调群。
回想一下,生成圆的点集的参数形式如下:
\(x=a+rcos(θ), y=b+rsin(θ)\) ,其中 \((a, b)\) 是圆心, \(θ\) 是 0 到 \(2π\) 的参数,而 \(r\) 是半径。
下面的代码将生成并绘制采样圆的离散点
import numpy as np
import matplotlib.pyplot as plt
n = 30 #number of points to generate
##generate space of parameter
theta = np.linspace(0, 2.0*np.pi, n)
a, b, r = 0.0, 0.0, 5.0
x = a + r*np.cos(theta)
y = b + r*np.sin(theta)
##code to plot the circle for visualization
plt.plot(x, y)
plt.show()
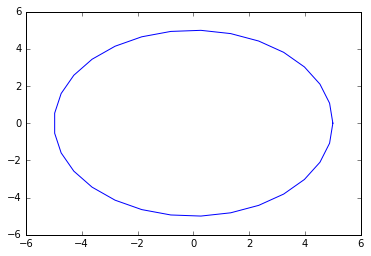
好吧,让我们从这个 (有点) 完美的圆圈中随机取样,顺便加点误差。
x2 = np.random.uniform(-0.75,0.75,n) + x #add some "jitteriness" to the points
y2 = np.random.uniform(-0.75,0.75,n) + y
fig, ax = plt.subplots()
ax.scatter(x2,y2)
plt.show()
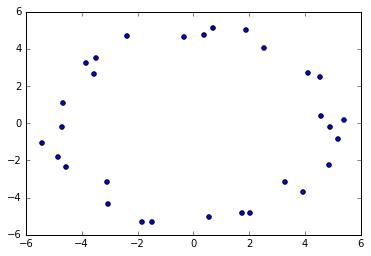
很明显,生成的点看起来是 “圆”,因为在这里它是有一个洞的明显的循环的圈,所以我们想要我们的单纯复形捕捉到这个属性。
让我们用以下步骤慢慢分解 VR 复形的结构:
- 定义距离函数 \(d(a,b) = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2}\) (欧几里得距离)
- 为构建 VR 复形建立参数 \(ϵ\)
- 建立一个点云数据的集合(用 python 的 list,最接近集合的结构),这将是 0 维单纯形的复形。
- 扫描每一对点,计算点之间的距离。如果两点距离小于 \(ϵ\) ,我们就给这两个点连一条线,这时我们会获得一个 1 维复形。
- 如果我们计算了所有距离并画好一个图,我们可以遍历每一个顶点,识别它们的邻点并尝试递增地建立高维复形(在 1 维复形中加入所有 2 维复形,再加入所有维复形,依此类推)。
有很多算法可以从数据中构建一个单纯复形(除了 VR 复形,还有很多其他类型的单纯复形)。不幸的是,以我了解,这世上没有从点数据中创建一个完整的(不是向下采样的)单纯复形的多项式时间复杂度的算法。因此,无论如何,一旦我们开始处理真正的大数据集,构建复形将变成计算代价相当高的行为 (甚至令人望而却步)。在这方面,我们需要做更多的工作。
我们将使用 Afra Zomorodian 的 “快速构建 VR 复形” 的算法。这个算法有两个主要步骤。
- 构造点集数据的邻域图。领域图是无向加权图 \((G, w)\) ,其中 \(G=(V, E)\) , \(V\) 是顶点集, \(E\) 是边集,而 \(w:E→\mathbb R\) ( \(w\) 是每个边到实数的映射,这是权重)。我们的边是通过连接一些我们曾互相定义过距离(用参数 \(\epsilon\) )的点创造的。特别的,
\(E_{\epsilon} = \{\{u,v\} \mid d(u,v) \leq \epsilon, u \neq v \in V\}\)
其中 \(d(u, v)\) 是两个点 \(u, v∈V\) 的度量 / 距离函数。而权重函数简单地将每条边的权值设为等于边的两个点之间的距离。也就是, \(w(\{u,v\}) = d(u,v), \forall \{u,v\} \in E_{\epsilon}(V)\) 。
- 在第一步生成的领域图形成 VR 扩张。给定一个领域图 \((G, w)\) ,VR 复形 \((R(G), w)\) (其中 \(R\) 是 VR 复形)权重过滤通过下列方式给定:
\(R(G) = V \cup E \cup \{ \sigma \mid \left ({\sigma}\above 0pt {2} \right ) \subseteq E \} ,\)
对于 \(σ∈R(G)\) ,
\(w(\sigma) = \left\{ \begin{array}{ll} 0, & \sigma = \{v\},v \in V, \\ w(\{u,v\}), & \sigma = \{u,v\} \in E \\ \displaystyle \operatorname*{max}_{\rm \tau \ \subset \ \sigma} w(\tau), & otherwise. \end{array} \right\}\)
这是什么意思?在这个简单的例子中,我们准备从我们的领域图(左)中获得 VR 复形(右):

所以上面的算法是说维 VR 复形是领域图中所有顶点和边线并的集合,也是所有在 E 的单纯形 \(\sigma\) 中每种两个顶点可能的组合的并。
下面的部分给所有 VR 复形的每个单纯形,从单个 0 维单纯形到高维单纯形,定义了权重函数。如果单纯形是 0 维单纯形(只有顶点),那么单纯形的权重是 0。如果单纯形是 1 维单纯形(有边),那么权重是两点之间的距离。如果单纯形是高维单纯形,如 2 维单纯形(三角形),那么权重是单纯形中最长边的权重。
在我们计算我们 “圈形” 数据的 VR 复形之前,让我们给上面出现过的单纯形进行一个全面检查。我们先在 \(\mathbb R^2\) 中嵌入顶点,然后尝试先去构建领域图。
raw_data = np.array([[0,2],[2,2],[1,0],[1.5,-3.0]]) #embedded 3 vertices in R^2
plt.axis([-1,3,-4,3])
plt.scatter(raw_data[:,0],raw_data[:,1]) #plotting just for clarity
for i, txt in enumerate(raw_data):
plt.annotate(i, (raw_data[i][0]+0.05, raw_data[i][1])) #add labels
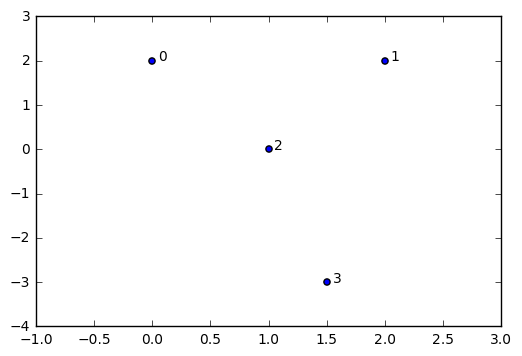
我们将用原始数据数组中的索引号来表示我们单纯复形中的每个顶点。例如点 \([0, 2]\) 出现在我们数据数组的开头,因此我们把它当作单纯复形中的参考点。
##Build neighorbood graph
nodes = [x for x in range(raw_data.shape[0])] #initialize node set, reference indices from original data array
edges = [] #initialize empty edge array
weights = [] #initialize weight array, stores the weight (which in this case is the distance) for each edge
eps = 3.1 #epsilon distance parameter
for i in range(raw_data.shape[0]): #iterate through each data point
for j in range(raw_data.shape[0]-i): #inner loop to calculate pairwise point distances
a = raw_data[i]
b = raw_data[j+i] #each simplex is a set (no order), hence [0,1] = [1,0]; so only store one
if (i != j+i):
dist = np.linalg.norm(a - b) #euclidian distance metric
if dist <= eps:
edges.append({i,j+i}) #add edge
weights.append([len(edges)-1,dist]) #store index and weight
print("Nodes: " , nodes)
print("Edges: " , edges)
print("Weights: ", weights)
Nodes: [0, 1, 2, 3]
Edges: [{0, 1}, {0, 2}, {1, 2}, {2, 3}]
Weights: [[0, 2.0], [1, 2.2360679774997898], [2, 2.2360679774997898], [3, 3.0413812651491097]]
完美。现在我们有一个结点集,边集和一个权重集,这所有构成了我们的领域图 \((G, w)\) 。我们的下一个任务是用邻域图构建高维单纯形。在这种情况下,我们只有一个额外的 2 维单纯形(三角形)。我们需要设置一些基础的方法。
def lower_nbrs(nodeSet, edgeSet, node):
return {x for x in nodeSet if {x,node} in edgeSet and node > x}
def rips(nodes, edges, k):
VRcomplex = [{n} for n in nodes]
for e in edges: #add 1-simplices (edges)
VRcomplex.append(e)
for i in range(k):
for simplex in [x for x in VRcomplex if len(x)==i+2]: #skip 0-simplices
#for each u in simplex
nbrs = set.intersection(*[lower_nbrs(nodes, edges, z) for z in simplex])
for nbr in nbrs:
VRcomplex.append(set.union(simplex,{nbr}))
return VRcomplex
好的,让我们来试试它能不能用。假设我们要将所有的单纯形都提升到 \(3\) 维。
嗯,看起来很完美。
现在我们想看看它是什么样的。我写了一些代码,它能根据我们 VR 算法的输出绘制单纯复形。但这对于理解 TDA 并不重要 (大多数情况下,我们不会尝试可视化单纯复形,因为它们太过高维),因此我不会尝试解释绘制图形的代码。
plt.clf()
plt.axis([-1,3,-4,3])
plt.scatter(raw_data[:,0],raw_data[:,1]) #plotting just for clarity
for i, txt in enumerate(raw_data):
plt.annotate(i, (raw_data[i][0]+0.05, raw_data[i][1])) #add labels
##add lines for edges
for edge in [e for e in theComplex if len(e)==2]:
pt1,pt2 = [raw_data[pt] for pt in [n for n in edge]]
print(pt1,pt2)
line = plt.Polygon([pt1,pt2], closed=None, fill=None, edgecolor='r')
plt.gca().add_line(line)
##add triangles
for triangle in [t for t in theComplex if len(t)==3]:
pt1,pt2,pt3 = [raw_data[pt] for pt in [n for n in triangle]]
line = plt.Polygon([pt1,pt2,pt3], closed=False, color="blue",alpha=0.3, fill=True, edgecolor=None)
plt.gca().add_line(line)
plt.show()
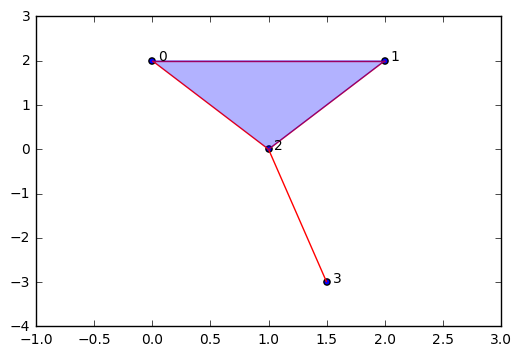
现在我们对我们非常简单的 VR 复形有一个很好的描述。现在我们知道该怎么做。我们需要了解单纯同调,一种关于单纯形和复形拓扑不变量的研究。特别是,我们希望用数学方法辨认 \(n\) 维连通的组件,圈和孔。为了帮助这些工作,我重新打包了我们在上面使用的代码作为一个单独的文件,这样我们就可以直接导入它,并方便地使用我们的数据上的函数。你可以在这里下载最新的代码:<https://github.com/outlace/OpenTDA/blob/master/SimplicialComplex.py>
在这里,我将从我们从一个圆中取样的 (抖动的) 点上压缩我们的 \(x\) 和 \(y\) 坐标,这样我们就可以用它来构建一个更复杂的单纯复形。
newData = np.array(list(zip(x2,y2)))
import SimplicialComplex
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=3.0)
ripsComplex = SimplicialComplex.rips(nodes=graph[0], edges=graph[1], k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)
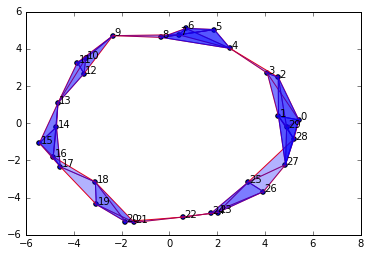
整洁如约!很明显,我们已经复制了采样点的圆形空间。注意,这里有 1 维单纯形和更高维的单纯形,但它形成了用单个洞连接的组件。
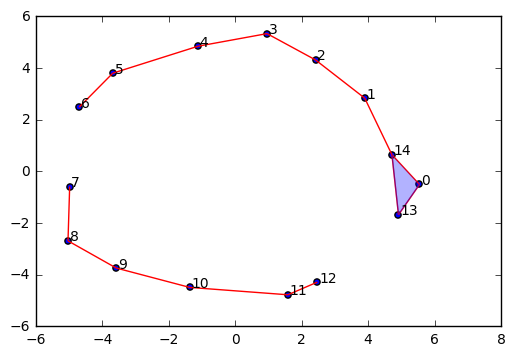
如果我们将半径参数 \(\epsilon\) 减短过多,就会变成下图的样子:
同调群¶
既然我们已经知道什么是单纯复形,以及如何从原始数据中生成它们,我们就需要进一步计算这些单纯复形有趣的拓扑特征。
以计算同调为形式的拓扑数据分析给了我们一种在我们基于数据集建立的拓扑空间(通常是单纯复形)中识别组件和 \(n\) 维 “孔”(如圆中间的孔)的数量的方法。
在我们继续之前,我想去描述一种可以加在我们已经用过的单纯复形上的额外属性。我们可以给它一个定向的性质。一个定向的单纯形 \(σ=u_1, u_2, u_3, …u_n\) 是通过它的顶点顺序定义的。因此,定向单纯形 \(\{a, b, c\}\) 和定向单纯形 \(\{c, b, a\}\) 是不同的。在绘制低维图像时,我们可以通过将边缘变成箭头来描述它。
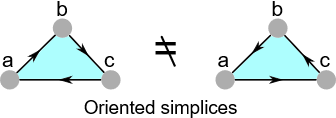
现在,严格地说一个数学集合 (用曲线括号表示) 是一个无序的对象集合,所以为了在单纯形上加入方向,我们需要增加一些额外的数学结构,如通过在元素间加入二元的≤关系使顶点的集合成为有序集。但这并不值得深入研究,我们只需要假设顶点集是有序的,不需要大张旗鼓地声明额外的结构必须精确定义其顺序。
回头看看上面的两个单纯形,我们可以发现这两个单纯形箭头的方向是相反的。假设左边那个单纯形是 \(σ_1\) ,右边那个单纯形是 \(σ_2\) ,我们可以说 \(σ_1=-σ_2\) 。
引入方向的原因将会在后面清楚地说明。
\(n\) 维链¶
记住,一个单纯复形包含了这个复形中每一个最高维度的单纯形的所有面。也就是说,如果我们有一个 \(2\) 维复形(一个拥有最高维度单纯形的单纯复形是 \(2\) 维单纯形(三角形)),那这个复形也包含了所有比它低维的面(如边和顶点)。
\(C=\{\{0\}, \{1\}, \{2\}, \{3\}, \{0, 1\}, \{0, 2\}, \{1, 2\}, \{2, 3\}, \{0, 1, 2\}\}\) 是由一个点云 (例如数据集) 构成的单纯复形结构, \(X=\{0, 1, 2, 3\}\) 。
\(C\) 是一个 \(2\) 维复形,因为它最高维的单纯形是 \(2\) 维单纯形(三角形)。我们可以把这个复形分解成一系列的子集,其中每组都由所有 \(k\) 维单纯形组成。在单纯同调理论中,这些组叫做链群,并且任意特定组是 k 维链群 \(C_k(X)\) 。例如 \(C\) 的 \(1\) 维群组是 \(C_1(X)=\{\{0, 1\}, \{0, 2\}, \{1, 2\}, \{2, 3\}\}\) 。
抽象代数基础¶
“链群”中的 “群” 事实上有一个特定的数学意义。“群”的概念来自抽象代数,一个概括了你高中代数课上学过的课题的数学领域。不用说,它很抽象,但我会尽力从一些容易概念化的具体例子开始,然后才慢慢抽象出来,得到最基础的概念。我将覆盖到群,环,域,模,向量空间和各种其他小主题,当他们出现的时候。一旦我们解决了这些问题,我们将会到链群的讨论中。
群¶
被称为群的数学结构可以被认为是对对称概念的概括。有一个完善的研究群的数学体系叫群论。我们不会在这里深入研究群,因为我们只需要知道我们需要知道的。为了我们的目的,群是一个具有对称性的数学对象。从几何学的角度来说,这可能是最容易理解的,但你会发现,群是如此普遍,以至于许多不同的数学结构都可以从群论的角度受益。
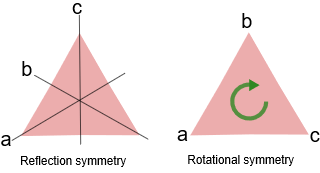
目测我们可以在这个三角形上看到一些不改变结构的可能的操作。我画了对称线,这表示你可以在这 \(3\) 条线上镜像,最后还是得到同样的三角形结构。更重要的是,你可以在平面上转化这个三角形并且仍然是相同的结构。你也可以将三角形旋转 \(120\) 度,它仍然保持三角形的结构。群论为管理这些类型的操作及其结果提供了精确的工具。
这是群的数学定义:
群:是集合 \(G\) 和一个二元运算 \(*\) (或者其他你喜欢的符号),这一运算将 \(a, b\in G\) 映射到 \(c\in G\) 上,写作 \(a*b=c, \forall a, b, c \in G\) 。这个集合和它的运算被写成有序对 \((G, *)\) 。另外,为了成为一个有效的群,集合和运算必须满足以下条件:
1. 结合律: \(\forall a, b, c\in G, (a*b)*c=a*(b*c)\)
2. 单位元:存在一个元素 \(e \in G\) ,使得所有元素 \(a \in G\),等式 \(a*e=e*a=a\) 成立。这样的元素是唯一的,被称为单位元素。
3. 逆元:对于所有 \(a\in G\) ,存在一个元素 \(b\in G\) ,通常表示为 \(a^{-1}\) ,使得 \(a*b=b*a=e\) ,其中 \(e\) 是单位元素。
备注:运算 \(*\) 不一定可以交换,即 \(a*b=b*a\) 不一定成立。运算的顺序可能有关系。如果没有关系,则称之为交换群。集合 \(\mathbb Z\) (整数集)和加法是一个交换群,因为 \(1+2=2+1\) 。
“群”的概念看起来很随意让人不禁想问用途何在,但现在我们有希望把这个讲清楚些。记住,所有的数学对象都是由一些 (看似任意的) 公理集合(基本上定义结构的规则集必须遵守)。你可以在集合上定义任何您想要的结构(只要它们逻辑一致而且有统一规则),那你将需要一些数学对象 / 结构。有些结构比其他的更有趣。有些集合有很多结构(比如很多规则),而有的则很少。通常,具有许多规则的结构仅仅是更通用 / 抽象结构的专门化。群只是一些数学结构(被人为赋予了规则的集合),具有有趣的属性,并且在很多领域都很有用。但是由于他们是如此的普遍,所以有时比较难确切地解释他们。
让我们看看我们能不能从上面 “群化” 我们的三角形示例。我们可以把三角形看作是一组被标记的顶点,就当它是 \(2\) 维单纯形。既然我们已经标记了三角形的顶点,我们可以很容易地把它描述为集合:
但是我们如何定义 \(t\) 的二元运算?我不确定,让我们试一试。我们将构建一个表,它会向我们展示当我们在 \(t\) 中 “运算” 两个元素时会发生什么。我认真的完成以下二元运算 \(\{(a, b)的映射|a, b\in t \}\) 并看看它是不是有效的群。如下图。
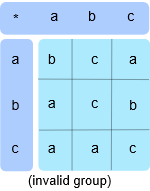
为了了解 \(a*b\) 是什么,你从第一行开始看,找到 \(a\) ,然后在左列找到 \(b\) ,它们相交的地方即是结果。在我举的例子中, \(a*b=a\) 。注意,我已经定义了这个操作是不可交换的,所以 \(a*b≠b*a\) 。你必须从上一行开始,然后到左边的行 (按顺序)。
现在你应该能够很快地看出,这实际上不是一个有效的群,因为它违反了群的公理。例如元素 \(b\in t\) ,你找不到一个单位元素 \(e\) ,使得 \(b*e=b\) 。
所以我们再来一次。这一次,我想要创建一个有效的群。
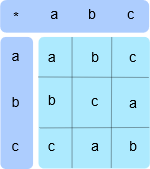
你应该检查一下,这实际上是一个有效的群,这一次这个群是可交换的,所以我们称它为交换群。单位元素是 \(a\) ,因为 \(a*b=b*a=b,a*c=c*a=c\) 。注意,表格本身目测就能看出来有对称性。
结果表明,有限的群,就像有限的拓扑空间一样,可以被表示为有向图,这有助于可视化 (数学的模式很漂亮,不是吗?) 这些群的图有一个特殊的名称: Cayley 图。构造一个 Cayley 图比构造拓扑空间的图要复杂得多。我们必须向 Cayley 图形添加另一个属性,除了直接使用箭头 (边),我们还为每个箭头分配一个运算。因为如果箭头从 \(a\) 指向 \(b\) ,表示在群中, \(a\) 运算生成 \(b\) 。并不是所有的箭头都是相同的运算,所以在可视化的帮助下,我们通常会使每一种类型的运算都与一个不同颜色的箭头相关联。
在我们构建一个 Cayley 图之前,我们需要了解一个群的生成集是什么。记住,群 \((G, *)\) 是集合 \(G\) 加二元运算 \(*\) 。生成集是子集 \(S \subseteq G\) ,比如 \(G = \{a * b \mid a,b \in S\}\) 。总之,这说明生成集 \(S\) 是 \(G\) 的子集,但如果我们在 \(S\) 的元素中实现二元运算 \(*\) ,很可能它就变成完整的集合 \(G\) 。就好像说 \(S\) 是 \(G\) 的压缩。可能存在很多生成集。那我们的集合 \(t={a, b, c}\) 和运算 \(*\) 的生成集该怎么定义呢?好,看一下运算表部分,我已经用红色标出了。
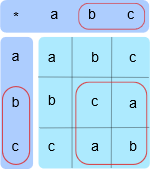
你发现我标出了子集 \(\{b, c\}\) ,因为这两个元素可以生成完整的集合 \(\{a, b, c\}\) 。但是事实上 \(\{b\}\) 和 \(\{c\}\) 也能分别生成完整的集合。例如, \(b*b=c,b*b*b=a\) (我们也可以写成 \(b^2=c\) 和 \(b^3=a\) )。同样, \(c*c=b,c*c*c=a\) 。因此,通过在 \(b\) 或者 \(c\) 上反复使用运算 \(*\) ,我们可以生成集合的三个元素。而 a 是集合的单位元素,所以 \(a^n=a, n \in N\) 。
因为存在两个可能性来生成元, \(b\) 和 \(c\) ,所以这里有两种不一样的箭头,代表不一样的运算。也就是说,我们有 “ \(b\) ” 箭头和 “ \(c\) ” 箭头(代表 \(*b\) 和 \(*c\) )。为了构建群 \((G, *)\) 的 Cayley 图的边集 \(E\) ,生成集 \(S \subseteq G\) 是边集 \(E = \{(a,c) \mid c = a* b \land a,c \in G \land b \in S\}\) 其中每条边都被 \(b∈S\) 用颜色标记。
Cayley 图的结果是:
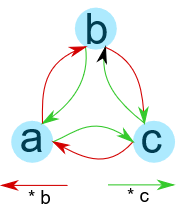
在这个 Cayley 图中,我们为两个生成元 \(b\) 和 \(c\) 画了两种箭头,然而,我们只需要选其一种,因为只要一种就能生成整个群。所以,一般来说,我们只要选最小的生成元来画 Cayley 图,这种情况下,我们只需要红色箭头就够了。
所以这个群是等边三角形的旋转对称,因为我们可以旋转三角形 \(120\) 度而不改变它,那我们的群将 \(120\) 度的每一次循环表示为 “加”( \(*\) ) 生成元 \(b\) 的群运算。我们还可以加单位元素,这看起来就像不旋转它一样。在这我们能看出这基本集合 \(\{a, b, c\}\) 中的元素 “加” \(b\) 是怎么看起来像顺时针旋转 \(120\) 度的:
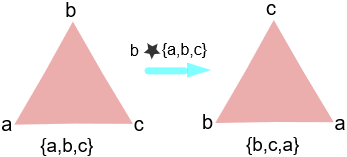
这也被叫做与 \(\mathbb Z_3\) 同构的 \(3\) 阶循环群。 \(\mathbb Z_3\) ?同构?你都在问什么?
同构主要是在保持结构的两个数学结构之间存在一对一 (双射) 映射。这就像它们是一样的结构但是有不同的标签一样。我们刚研究的三角形的旋转对称群是与整数模 \(3\) ( \(\mathbb Z_3\) )同构的。模运算意味着在某一点上,运算循环回到开始。不像整数 \(\mathbb Z\) ,如果你一直加 \(1\) ,你会得到一个更大的数,在模运算中,最终你加 \(1\) 会回到起始元素 (单位元素 \(0\) )。想想时钟的时针,它是整数模 \(12\) ( \(\mathbb Z_{12}\) ),因为如果你再增加一个小时它最终会循环回来。
这是整数模 \(3\) 的加法表:
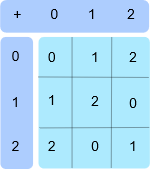
所以,在 \(\mathbb Z_3\) 中, \(1+1=2\) ,但 \(2+2=1\) ,而 \(1+2=0\) 。整数模 \(x\) 形成一个循环群 (带有一个生成元),其中元素 \(x\) 和 \(0\) 是单位元素。
好了,这就是群的基本知识,让我们继续讨论环和域。
环和域¶
现在我们继续学习一些关于环的知识,然后再轮到域。提前声明,域和环是群的特例,也就是说,它们是带有群规则和附加规则的集合。所有环都是群,所有域都是环。
环:是定义了两个二元运算 \(*\) 和 \(\bullet\) 的集合 \(R\) ,它满足下面这三个公理(环公理):
1. \(R\) 在 \(*\) 运算下是交换群,也就是 \((R, *)\) 满足群的公理。
2. 当运算 \(\bullet\) 满足结合律 \((a\bullet (b\bullet c)=(a\bullet b)\bullet c)\) 并且 \((R, \bullet)\) 有单位元素 \((\exists e \in R 满足e\bullet b=b\bullet e=e)\) 时, \((R, \bullet)\) 构成一种叫幺半群的数学结构。
3. \(*\) 和 \(\bullet\) 满足分配律,即 \(a, b, c\in R\) ,有:
\(a\bullet (b*c)=(a\bullet b)*(a\bullet c)\) (左分配律)
\((b*c)\bullet a=(b\bullet a)*(c\bullet a)\) (右分配律)
最著名的环是 \(\mathbb Z\) ,因为它有两个熟悉的运算 \(+\) 和 \(\times\) 。因为环也是群,我们提到整数群的生成元。因为整数从 \(\{ -n…-3, -2, -1, 0, 1, 2, 3…n\}\) 跨度很大,所以在加法运算( \(+\) )中,存在两个生成元 \(\{ -1, 1\}\) ,因为我不停 \(1+1+1+…\) 可以得到所有正整数,而 \(-1+-1+-1+…\) 可以得到所有负整数,并且 \(-1+1=0\) 。
而下面是域的定义。
域:是定义了两个二元运算 \(*\) 和 \(\bullet\) 的集合 \(F\) ,对于 \(\forall a, b, c\in F\) ,它满足以下条件。
结合律 \(a*(b*c)=(a*b)*c, a\bullet (b\bullet c)=(a\bullet b)\bullet c\) 交换律 \(a*b=b*a, a\bullet b=b\bullet a\) 分配律 \(a\bullet (b*c)=(a\bullet b)*(a\bullet c), (b*c)\bullet a=(b\bullet a)*(c\bullet a)\) 恒等 \(a*0=a=0*a, a\bullet 1=a=1\bullet a\) 逆元素 \(a*(-a)=0=-a*a, a\bullet a^{-1}=1=a^{-1}\bullet a\) ,如果 \(a≠0\)
其中 \(0\) 是 \(*\) 运算下的单位元素, \(1\) 是 \(\bullet\) 运算下的单位元素。
显然,一个域的需求要比一个群多得多,为了注意,我一直在用符号 \(*\) 和 \(\bullet\) 作为群,环,域的二元运算,但更常用的是 \(+\) 和 \(\times\) 。我最初不使用这些符号的唯一原因是我想强调指出,这些符号并不仅仅适用于你所熟悉的数字,而是抽象的运算,它可以在满足要求的任何数学结构上起作用。但是现在你明白了,我们可以用更熟悉的符号。所以 \(+=*\) , \(×=\bullet\) ,而 \(a÷b=a×b^{-1}\)
还记得整数集 \(\mathbb Z\) 是最熟悉的环吗?整数集不构成域,因为在 \(\mathbb Z\) 中,不是每个元素都有它的逆元素。例如,如果 \(\mathbb Z\) 是域,那么 \(5×5^{-1}=1\) ,然而 \(5^{-1}\) 不是整数。如果我们考虑的是实数集 \(\mathbb R\) ,那 \(5^{-1}=1/5\) 。因此,一个通过加( \(+\) )和乘( \(×\) )定义的域,同时也暗中定义了减( \(-\) )和除( \(\div\) )。所以如果一个集合是域,除了单位元素,所有元素都能进行除运算;正如你从小学就知道 \(0\) 不能作除数一样。而且这一切都是对称的,加法中 \(1\) 的逆元素是 \(-1\) , \(2\) 的逆元素是 \(-2\) 。
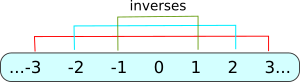
注意到逆的对称性了吗?每一组互逆的数都与集合的中心,即为 \(0\) ,距离相等。但因为 \(0\) 是中心,所以它没有逆,也不能用除法来定义。
所以退一步说,群论是关于研究对称性的。任何具有对称特征的数学对象都可以被编组为群,然后用代数方法来确定哪些保持对称的操作可以在群中进行。如果我们不关心对称性,我们只想研究具有二元运算和结合律的集,那么我们可以研究幺半群。
为什么我们要学习群、环和域?¶
好的,我们学习了群、环、域的基础,但为什么呢?我已经说过了,我们需要理解群来理解那些需要计算单纯复形的同调的链群。但更普遍的是,群、环和域让我们在任何数学对象上都能使用我们熟悉的高中代数工具,这些工具满足群 / 环 / 域(不只是数字)相对宽松的需求。所以我们能对像单纯复形这种数学对象进行加,减(群),乘(环),除(域)。此外,我们还可以用一些未知的变量来解方程,包括不是数字的抽象数学对象。
直观上,向量是 n 维的数字列表,例如 \([1.2, 4.3, 5.5, 4.1]\) 。重要的是,我确信您已经了解了将向量相加并将它们乘以标量的基本规则。例如,
… 总之,在向量加法中,它们必须是相同的长度,然后相应的元素相加。也就是说,每个向量的第一个元素加在一起,等等。而对于标量…
… 向量中的每个元素都乘以标量。
但等等!向量的定义没有提到任何信息说向量的元素是数量或列表。向量可以是一个符合域标准的任何有效的数学结构的集合。只要向量空间的元素可以通过域的元素(通常是实数或者整数)放大或缩小,并加在一起生成新的元素,而这新的元素仍是向量空间中的元素。
这是向量空间的正式定义,一种元素是向量的数学结构。
向量空间:在域 \(F\) 上的向量空间 \(V\) 是被叫做向量的对象的集合,其中向量能和标量进行加减乘除运算。因为 \(V\) 和加运算构成交换群,而对于任意 \(f \in F, v \in V\) ,我们都有元素 \(fv \in V\) ( \(f×v\) 的结果仍在 \(V\) 中)。标量乘法是分配律和结合律,而域的乘法恒等式在向量上恒等。
例如,最熟悉的数字向量来自域 \(\mathbb R\) 的向量空间。
那么,模 和向量空间一样,除了它是在环上定义的以外。记住,每个域都是环,所以相较于向量空间,模是一个更随意(更普遍)的数学结构。
(修改自 < http://www.math.uiuc.edu/~r-ash/Algebra/Chapter4.pdf >)
我们还应该讨论向量空间 (或模) 的基础。
我们有一个有限集 \(S=\{ a, b, c\}\) ,我们想用它来构建一个模(或者向量空间)。我们可以在环 \(R\) 上用这个集合构建模。在这种情况下,我们的模在数学上的定义是:
或者等效于
其中 \(*\) 是我们模的二元 “乘” 运算。但因为 \(R\) 是环,这必须还有第二个二元运算,我们可以叫它 “加”,用 \(+\) 表示。注意到我用的是圆括号,因此顺序很重要,例如 \((a, b, c)≠(b, a, c)\) 。
现在, \(M\) 中的每一个元素是以 \(\{ xa, yb, zc\}\) 的形式(为了方便,我们省略了 \(*\) ),因为它构成了这个模的基础。我们可以从它底层的环 R 中加和缩放每个元素 \(M\) 。如果我们用整数集 \(\mathbb Z\) 代替环,那我们可以通过下面方法来加和缩放:
\(m_1, m_2 {\in M} \\ m_1 = (3a, b, 5c) \\ m_2 = (a, 2b, c) \\ m_1 + m_2 = (3a+a, b+2b, 5c+c) = (4a, 3b, 6c) \\ 5*m_1 = 5 * (3a, b, 5c) = (5*3a, 5*b, 5*5c) = (15a, 5b, 25c)\)
如果我们只注意加运算,这个模也是一个群(因为每个模和向量空间都是一个群),但即使我们的生成集是一个像 \(\{ a, b, c\}\) 这样的有限集,一旦我们把它应用在像整数这样的无限环上,我们就构建了一个无限的模或向量空间。
通常情况下,一个向量空间,我们可以提出很多个基,然而,有一个数学定理告诉我们所有可能的基都是相同大小的。这就引出了维度的概念。向量空间 (或模) 的维数是其基的大小。因此,对于上面给出的例子,基的大小是 \(3\) (基有三个元素),因此模块的维度为 \(3\) 。
再如, \(\mathbb R^2\) 形成了一个向量空间,其中 \(\mathbb R\) 是实数集。这样定义: \(\mathbb R^2 = \{(x,y) \mid x,y \in \mathbb R\}\) 。基本上我们有所有可能的实数对组成的无限集。这个向量空间的一个基就是 \((x,y) \mid x,y \in \mathbb R\) ,这是理所应当的因为它最简单,但是没有人能阻止我们用 \((2x+1.55,3y-0.718) \mid x,y \in \mathbb R\) 作基,因为我们最终得到了相同的向量空间。但无论我们如何定义我们的基,它总是有 \(2\) 个元素,因此它的维数是 \(2\) 。
当我有一个像 \(\mathbb R^2\) 这样 \(2\) 维的向量空间,我们可以像这样分离它们的成分:
\(\mathbb R_x = \{(x, 0) \mid x \in \mathbb R\} \\ \mathbb R_y = \{(0, y) \mid y \in \mathbb R\} \\ \mathbb R^2 = \mathbb R_x \oplus \mathbb R_y\)
我们引入了新的符号,叫做 直和 \(\oplus\) ,用来表示通过像 \((x,0)+(0,y)=(x+0,0+y)=(x,y) \mid x,y \in \mathbb R\) 这样构建向量空间的维数的过程。因此我们可以简单的表示为 \(\mathbb R^2 = \mathbb R \oplus \mathbb R\) 。
我们也可以说 \(\mathbb R^2\) 的基是集合 \(\{ (1, 0), (0, 1)\}\) 的生成子空间,记作 \(span\{ (1, 0), (0, 1)\}\) 或者有时甚至更简单地用尖括号 \(<(1, 0), (0, 1)>\) 表示。 \(span\{ (1, 0), (0, 1)\}\) 是 “由基 \((1, 0)\) 和 \((0, 1)\) 的所有线性组合构成的集合” 的简写。
什么是线性组合?简单地说, \(x\) 和 \(y\) 的线性组合是 \(ax+by\) 形式的任何表达,其中 \(a, b\) 是域 \(F\) 中的常数。
因此 \((1, 0)\) 和 \((0, 1)\) 的其中一个可能的线性组合是:
\(5(1, 0)+2(0, 1)=(5*1, 5*0)+(2*0, 2*1)=(5, 0)+(0, 2)=(5+0, 0+2)=(5, 2)\) 。但 \((1, 0)\) 和 \((0, 1)\) 的所有线性组合可以用 \(\{a(1,0) + b(0,1) \mid a,b \in \mathbb R\}\) 来表达,而这等同于 \(span\{ (1, 0), (0, 1)\}\) 或者 \(<(1, 0), (0, 1)>\) 。这个集合所有的实数都是由 \(\mathbb R^2\) 表示的。
关于向量空间的基,重要的是它们必须是线性无关的。这意味着一个元素不能被表示成另一个元素的线性组合。例如,基本元素 \((1, 0)\) 不能被 \((0, 1)\) 表示。 \(\not\exists a,b \in \mathbb R \land a,b\neq 0\) ,使得 \(a(0,1) + b(1,0) = (1,0)\) 。
因此总结,向量空间的基 \(V\) 包含了元素 \(B\) 的集合,使得每个元素 \(b\in B\) 是线性无关的,而 \(B\) 的生成子空间生成整个向量 \(V\) 。因此向量空间的维度 \(dim(V)\) 是 \(B\) 中元素的个数。
(参考: The Napkin Project by Evan Chen <Evan Chen • Napkin>)
链群¶
哎,好吧,我们克服了很多障碍,但是现在我们回到我们真正关心的问题:算出一个单纯复形的同调群。您可能还记得,我们没有讨论单纯复形的链群。我不想重复所有的事情,所以,如果你忘记了,就把这部分重新读一遍。我会等你的…
让 \(S=\{\{a\}, \{b\}, \{c\}, \{d\}, \{a, b\}, \{b, c\}, \{c, a\}, \{c, d\}, \{d, b\}, \{a, b, c\}\}\) 成为一个从一些点云(如数据集)中构建的抽象的单纯复形(如下图所示)。 \(n\) 链 \((C_n(S))\) 是 \(n\) 维单纯形 \(S\) 的子集。比如 \(C_1(S)= \{a, b\}, \{b, c\}, \{c, a\}, \{c, d\}, \{d, b\}\}\) 和 \(C_2(S)=\{a, b, c\}\) 。
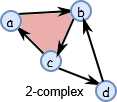
现在,如果我们给它定义一个满足群公理的二元加运算,让它可以变成一个链群。有了这个结构,我们可以把 \(C_n(S)\) 中的 \(n\) 维单纯形加在一起。更确切地说, \(n\) 链群是群、环或域 F 中 n 链带系数地相加。我准备用和 n 链一样的 \(C_n\) 符号来表示一个链群。
其中 \(σ_i\) 指的是 \(n\) 链 \(C_n\) 的第 \(i\) 个单纯形, \(a_i\) 是群、环或域的相应系数,而 \(S\) 是一开始的单纯复形。
技术上,任何域 / 群 / 环都可以被用来为链组提供系数,然而,就我们目的来说,最好用最简单的群是循环群 \(\mathbb Z_2\) ,即模 \(2\) 的整数。 \(\mathbb Z_2\) 只包含 \(\{ 0, 1\}\) 使得 \(1+1=0\) ,而且是域,因为我们可以定义一个加法和乘法运算来满足域的公理。这非常有用,因为我们只是希望能够说,在我们的 \(n\) 链中存在一个单纯形 (即它的系数为 \(1\) ) 或者不存在 (系数为 \(0\) ),如果我们有一个重复的单纯形,当我们把它们加在一起时,它们就会消掉。这就是我们想要的性质。你可能会反对,说 \(\mathbb Z_2\) 不是个群,因为它没有逆,例如 \(-1\) ,但事实上它是有的,例如, \(a\) 的逆是 \(a\) 。即在 \(\mathbb Z_2\) 中, \(a=-a\) 因为 \(a+a=0\) 。这就是逆存在的所有要求,你只需要在你的团队中有某个元素,满足 \(\exists b \in G, a+b=0, \forall b \in G\) ( \(G\) 是一个群)。
如果我们把 \(\mathbb Z_2\) 当作群系数,那我们基本上可以忽略单纯形的方向。这样就方便多了。但为了完整性,我想要融入方向,因为在学术论文和商业上,我见过很多人把整个整数集 \(\mathbb Z\) 当作系数;如果我们用一个像 \(\mathbb Z\) 一样带负数的域,那我们的单纯形需要有导向,就像 \([a, b]≠[b, a]\) 。这是因为如果我们用 \(\mathbb Z\) ,那么 \([a, b]=-[b, a]\) ,因为 \([a, b]+[b, a]=0\) 。
记住,我们的最终目标是在数学上找到单纯复形中的连通分支和 \(n\) 维的圈圈。我们上面的单纯复形 \(S\) ,目测,拥有一个连通分支和一个 \(2\) 维的圈或者孔。记住单纯形 \(\{a, b, c\} \in S\) 是 “被填充” 的,中间没有洞,这是一个固体。
我们现在开始定义边界映射。看起来一个无导向的 \(n\) 维单纯形 \(X\) 的边界映射(或者简称为边界)是 \(X\) 的 \({ {X} \choose {n-1}}\) 子集的集合。也就是说,边界是所有 \(X\) 的 \((n-1)\) 子集的集合。例如, \(\{ a, b, c\}\) 的边界是 \(\{\{a, b\}, \{a, c\}, \{b, c\}\}\) 。
让我们给出一个适用于定向单纯形的更精确的定义,并提供一些符号。
边界:带有方向向量 \([v_0,v_1,v_2,...v_n]\) 的 \(n\) 维单纯形 \(X\) 的边界( \(\partial(X)\) )是:
\[\partial(X) = \sum^{n}_{i=0}(-1)^{i}[v_0, v_1, v_2, \hat{v_i} ... v_n] \\\]其中第 \(i\) 个向量被从序列中移除。
单个顶点的边界是 \(0\) , \(\partial([v_i]) = 0\) 。
例如,如果 \(X\) 是 \(2\) 维单纯形 \([a,b,c]\) ,那么 \(\partial(X) = [b,c] + (-1)[a,c] + [a,b] = [b,c] + [c,a] + [a,b]\) 。
让我们来看看如何从边界的概念中得到上面 2 维复形中的一个简单的圈。我们看到 \([b,c]+[c,d]+[d,b]\) 是形成圈或者循环的 \(1\) 维单纯形。如果我们得到这个带有系数域 \(\mathbb Z\) 的集合的边界,那么
\(\partial([b,c] + [c,d] + [d,b]) = \partial([b,c]) + \partial([c,d]) + \partial([d,b]) \\ \partial([b,c]) + \partial([c,d]) + \partial([d,b]) = [b] + (-1)[c] + [c] + (-1)[d] + [d] + (-1)[b] \\ \require{cancel} \cancel{[b]} + \cancel{(-1)[b]} + \cancel{(-1)[c]} + \cancel{[c]} + \cancel{(-1)[d]} + \cancel{[d]} = 0\)
这使我们有了一个更普遍的属性,一个 \(p\) 圈是 \(C_n\) 中的 \(n\) 链,其中 \(C_n\) 的边界 \(\partial(C_n) = 0\) 。
也就是说,为了找到链群 \(C_n\) 中的 \(p\) 圈,我们需要解决代数方程 \(\partial(C_n) = 0\) ,而它的解就是 \(p\) 圈。不用担心,当我们过一些示例时,这些都会变得有意义和更直观的。
一个重要的结果是边界的边界总是 \(0\) ,即 \(\partial_n \partial_{n-1} = 0\) 。
链复形¶
我们刚看到边界运算是如何分配的,例如,两个单纯形 \(\sigma_1, \sigma_2 \in S\)
链复形: \(S\) 是一个单纯 \(p\) 复形。 \(C_n(S)\) 是 \(S\) 的 \(n\) 链, \(n≤p\) ,链复形 \(\mathscr C(S)\) 是
\[\mathscr C(S) = \sum^{p}_{n=0}\partial(C_n(S)) \\\]换句话说
\[\mathscr C(S) = \partial(C_0(S)) + \partial(C_1(S)) \ + \ ... \ + \ \partial(C_p(S)) \\\]
现在我们可以定义怎么在单纯复形中找到 \(p\) 圈。
核: \(\partial(C_n)\) 的核(记作 \(Ker(\partial(C_n))\) )是 \(n\) 链 \(Z_n \subseteq C_n\) 的群,其中 \(\partial(Z_n) = 0\) 。
我们已经快好了,我们需要再多两个概念,我们就可以定义单纯同调。
边界的像:边界 \(\partial_n\) (一些 \(n\) 链的边界)的像 \(Im(\partial_n)\) 是边界的集合。
例如,如果 \(1\) 链是 \(C_1 = \{[v_0, v_1], [v_1, v_2], [v_2, v_0]\}\)
然后 \(\partial_1 = [v_0] + (-1)[v_1] + [v_1] + (-1)[v_2] + [v_2] + (-1)[v_0]\)
\(Im \partial_1 = \{[v_0-v_1],[v_1-v_2],[v_2-v_0]\}\)
因此 \(\partial_n\) 和 \(Im\partial_n\) 唯一的不同是边界的像是集合形式的,而边界是多项式形式的。
第 \(n\) 个同调群:第 \(n\) 个同调群 \(H_n\) 定义为 \(H_n=Ker\partial_n/Im\partial_{n+1}\) 。
连通数:第 \(n\) 个连通数 \(b_n\) 定义为 \(H_n\) 的维度, \(b_n = dim(H_n)\) 。
更多群论¶
在这个点,我们再次掉进一个坑里,需要一些更多的说明和铺垫。我随便用了 \(/\) 来定义同调群 \(Ker\partial_n/Im\partial_{n+1}\) ,这个符号的数学用法是说,对于一些群 \(G\) 和 \(G\) 的子群 \(H\) , \(G/H\) 是商群。那什么是商群?我们需要学习更多群论内容。不幸的是,这很难,但是我会尽力让它简单易懂。
商群:对于群 \(G\) 和 \(G\) 的正规子群 \(N\) (记作 \(N \unlhd G\) ), \(G\) 在 \(N\) 上的商群,写作 \(G/N\) ,读作 “ \(G\) 以 \(N\) 为模”,是 \(N\) 在 \(G\) 中所有陪集的集合。
(来源:Weisstein, Eric W. "Quotient Group." From MathWorld--A Wolfram Web Resource. Quotient Group -- from Wolfram MathWorld)
现在你可以忽略一个正规子群的意思,因为我们将在 TDA 中处理的所有群都是交换群,而交换群的所有子群都是正规的。但这个定义是通过一个叫陪集的定义定义的。那什么是陪集呢?
陪集:对于一个群 \((G,*)\) ,考虑一个子群 \((H,*)\) 以及它里面的元素 \(h_i\) 和 \(G\) 的元素 \(x\) ,那么 \(x*h_i(\forall i=1,2,...)\) 组成子群 \(H\) 关于 \(x\) 的左陪集。
(来自:Weisstein, Eric W. "Left Coset." From MathWorld--A Wolfram Web Resource. Left Coset -- from Wolfram MathWorld)
那么我们可以思考子集 \(H≤G\) 关于一些元素 \(x\in G\) 的左(或右)陪集是什么,而这只是一个陪集,但如果我们有所有左陪集的集合(即对每个元素 \(x\in G\) 的陪集),那么我们就得到一个商群 \(G/H\) 。
对我们来说,我们只需要关注左陪集,因为 TDA 只包括交换群,而对于交换群,左陪集和右陪集是等价的。(我们将举一个非交换群的例子)
我们会重新考虑等边三角形和其对称性,以更好的了解的子群、 商群和陪集。

请记住,通过简单的可视化,我们确定了可以在保持其结构的等边三角形上执行的操作类型:我们可以将它旋转 \(0\) 、 \(120\) 、 \(240\) 度,我们可以通过三条对称的边翻转它。任何其他的操作,如旋转 \(1\) 度,都会在空间中产生不同的结构,例如, \(2\) 维欧几里得空间。
我们可以构建一个包括这六种操作的集合: \(S = \text{{\)rot_0\(, \(rot_{120}\), \(rot_{240}\), \(ref_a\), \(ref_b\), \(ref_c\)}}\) ... 其中 \(rot_0\) (等等)代表以中心将这个三角形旋转 0 度,而 \(ref_a\) 代表如上面图片,沿 \(a\) 边翻转。
例如,我们可以对这个三角形进行两种操作,如 \(rot_{120}\) 和 \(ref_a\) 。
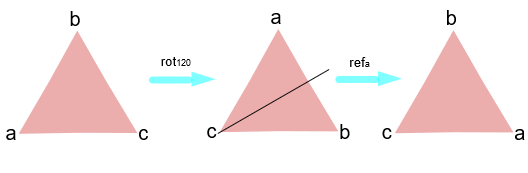
所以 \(S\) 形成有效的群了吗?它确实做到了,我们为它包含的每一对元素定义一个二元运算。而对任意 \(S\) 中的两个元素进行 \(a*b\) 运算是指 “先进行 \(a\) 操作,然后进行 \(b\) 操作”。 \(S\) 的元素是我们对三角形采取的操作。我们可以构建一个乘法表(或者 Cayley 表)来展示应用于每对元素的操作的结果。
这是 Cayley 表。

注意这定义了非交换 (非 abelian) 群,因为 \(a*b \neq b*a\) 。
现在我们可以使用 Cayley 表来构建一个 Cayley 图,并可视化群 \(S\) 。让我们回忆一下如何构建一个 Cayley 图。我们首先从顶点(或结点)开始,在群 \(S\) 中一个对应六个动作。然后我们需要算出这个群的最小生成元,也就是 \(S\) 最小的子集,在不同组合和重复应用群操作 \(*\) 后会生成完整的含有 \(6\) 个元素的集合 \(S\) 。你只需要 \(\{rot_{120}, ref_a\}\) 来生成整个集合,因此 \(2\) 个元素的子集是最小生成集。
现在,生成集中的每个元素被分配了不同颜色的箭头,因此,从结点 \(a\) 开始跟随特定的箭头到另一个元素 \(b\) 说明 \(a*g=b\) ,其中 \(g\) 是生成集中的元素。因此对于 \(S\) ,我们将有一个有两种不同类型的箭头的图,而我将给 \(rot_{120}\) 箭头涂蓝和给 \(ref_a\) 涂红。然后我们使用来自上面的 Cayley 表来连接节点和两种类型的箭头。
这是得到的 Cayley 图:
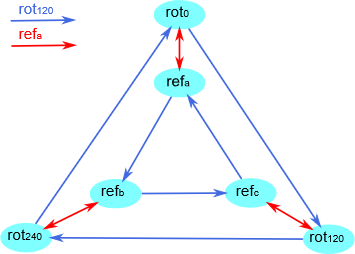
原来这个群是最小的有限非交换群,叫做 “ \(6\) 阶二面体群”,除了在等边三角形上的对称动作外,它还可以用来表示其他一些东西。
我们将参考这两个 Cayley 表和 Cayley 图,以得到先前我们给子群、陪集和商群定义的感觉。
让我们回到子群的概念。群 \((G,*)\) 的子群 \((H,*)\) (一般用 \(H\leq G\) 表示)只是 \(G\) 和同一满足群公理的运算 \(*\) 的子集。举个例子,每个群都有一个只有单位元素的子群(任何有效的子群都需要包含单位元素以满足组公理)。
考虑子群 \(W \leq S = \{rot_0, rot_{120}, rot_{240}\}\) 。它是一个有效的子群吗?是的,因为它是 \(S\) 的子集,包含单位元素,它是相联的,每个元素都有一个逆。在这个例子中,子群 \(W \leq S\) 形成了 Cayley 图中的外部循环(绿色结点):
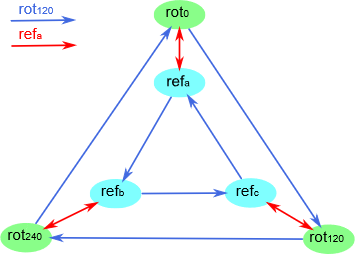
好的,一个子群相当直接了当。那么陪集呢?参照前面给出的定义,陪集是指一个特定的子群。因此我们考虑子群 \(W \leq S\) ,这个子群的陪集是什么?之前说过,我们只需要考虑左陪集,因为在 TDA 中这些群都是可交换的,这是事实,但等边三角形的对称群不是交换群,所以它们的左右陪集事实上是不一样的。我们只是用这个三角形来学习群论,一旦我们回到持续同调的链群,我们就会回到交换群。
回忆子集 \(H \leq S\) 的左陪集表示为 \(xH = \{x* h \mid \forall h \in H; \forall x \in G\}\) 。为了完整性,右陪集表示为 \(Hx = \{{h} * x \mid \forall h \in H; \forall x \in G\}\) 。
回到我们的三角对称,群 \(S\) 和它的子群 \(W\) 。记得 \(W \leq S = \{rot_0, rot_{120}, rot_{240}\}\) 。为了计算出左陪集,我们将通过选择 \(x\in S\) 开始,其中 \(x\) 不在子群 \(W\) 中。然后我们将拿 \(W\) 中的每个元素乘以 \(x\) 。我们将从 \(x = ref_a\) 开始。
所以 \(ref_a \star \{rot_0, rot_{120}, rot_{240}\} = \{ref_a \star rot_0, ref_a \star rot_{120}, ref_a \star rot_{240}\} = \{ref_a, ref_b, ref_c\}\) 。所以对于 \(ref_a\) 的左陪集是集合 \(\{ref_a, ref_b, ref_c\}\) 。现在,我们应该对另一个元素 \(x \in S, x \not\in W\) 进行同样的操作,但如果我们这样做,我们会得到同样的集合: \(\{ref_a, ref_b, ref_c\}\) 。因此我们只有一个左陪集。
对于我们这个子群,左右陪集是一样的,右陪集: \(\{rot_0\star ref_a, rot_{120}\star ref_a, rot_{240}\star ref_a \} = \{ref_a, ref_b, ref_c\}\)
(参考: < http://www.math.clemson.edu/~macaule/classes/m16_math4120/slides/math4120_lecture-3-02_handout.pdf >)
有趣的是,由于所有的 Cayley 图本身都具有对称性,所以在一般情况下,子群的左陪集就像在 Cayley 图中的子群的复制体一样。如果你考虑子集 \(W \leq S = \{rot_0, rot_{120}, rot_{240}\}\) ,它在 Cayley 图中形成这个外环,而左陪集则是构成图内部 “环” 的顶点集合。因此,这就像他们之间互相复制一样。这是另一个子群是 \(\{rot_0, ref_a\}\) 的例子:
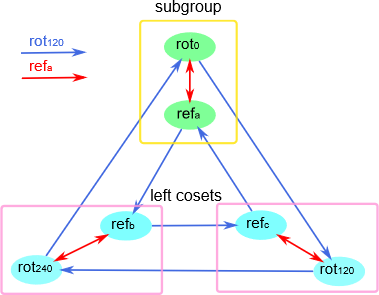
因此我们开始看到群的子群的左陪集是如何均匀地将群分成相同形式的几个子群的。子群是 \(W \leq S = \{rot_0, rot_{120}, rot_{240}\}\) ,我们可以将群 \(S\) 分成两份都是 \(W\) 形式的子群,而如果子群是 \(\{rot_0, ref_a\}\) , 我们可以将群 \(S\) 分成三份都是 \(W\) 形式的子群。
这直接引出了商群的概念。回想一下前面给出的定义:
对于群 \(G\) 和 \(G\) 的正规子群 \(N\) (记作 \(N \unlhd G\) ), \(G\) 在 \(N\) 上的商群,写作 \(G/N\) ,读作 “ \(G\) 以 \(N\) 为模”,是 \(N\) 在 \(G\) 中所有陪集的集合。
一个正规子群是左右陪集相同的子群。因此,我们可以发现,子群 \(W \unlhd S = \{rot_0, rot_{120}, rot_{240}\}\) 是正规子群。我们可以用它来构造商群, \(S/W\) 。
现在我们知道了什么是陪集,那么找到 \(S/W\) 就变得很简单了,它只是关于 \(W\) 的陪集的集合,而我们也将计算出来,陪集就是: \(S/W = \{\{rot_0, rot_{120}, rot_{240}\}, \{ref_a, ref_b, ref_c\}\}\) (我们将子群本身包含在集合中,因为子群的陪集严格地说包括了自己)。
这有两个非常有趣的原因, \(S/W\) 的结果是含有两个元素的集合(元素本身是集合),所以某种意义上,我们取了一个六个元素的原始集合(整个群),并将它分成了含有三个元素的集合,每个元素是含有两个元素的集合。看起来很熟悉吗?其实这很像简单的算术 \(6/3=2\) 。这是因为,实数的除法就是用陪集和商群定义的。第二个很有趣的原因是,商群中的两个元素是三角形的两种基本操作,即旋转操作和翻转操作。
我还想指出,我们得到的商群 \(S/W\) 实际上是一个群,也就是说,它满足了所有的群公理,在这个例子中,它与模 \(2\) 的整数( \(\mathbb Z_2\) )同构。
所以直观地说,当你需要一些商群 \(A/B\) ,其中 \(B\ \unlhd A\) ( \(B\) 是 \(A\) 的子群),只需要问自己,“我怎么把 \(A\) 分成像 \(B\) 一样的小块呢?” 并且分块可以重复。在这种情况下,我们的分块是不重叠的,即,商群中的每一个陪集都没有相同的元素,但情况并非总是如此。考虑由一个生成元生成的循环群 \(\mathbb Z_4\) :
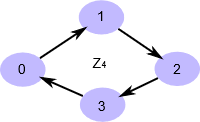
我们可以把这个群分成 \(2\) 个部分,但实际上有两种方法。我们可以生成一个子群 \(N \leq \mathbb Z_4 = \{0,2\}\) ,这将空间分成两个部分(有两个左陪集,因此我们的商群大小为 \(2\) )。我们在下面描述了这一点,其中每个 “部分” 是在 Cayley 图中 “彼此相对” 的一对元素。
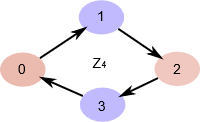
\(N = \{0,2\} \\ N \leq \mathbb Z_4 \\ \mathbb Z_4\ /\ N = \{\{0,2\},\{1,3\}\}\)
但我们也可以选择子群 \(N \leq \mathbb Z_4 = \{0,1\}\) ,其中每一对元素都是相邻的。在这种情况下,我们可以将群分成 \(4\) 个部分(即左陪集或商群的集合有 \(4\) 个元素)。
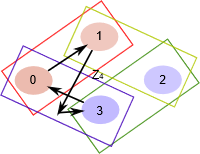
\(N = \{0,1\} \\ N \leq \mathbb Z_4 \\ \mathbb Z_4\ /\ N = \{\{0,1\},\{1,2\},\{2,3\},\{3,0\}\}\)
最后我想说的是代数闭群和非闭群的概念。基本上,一个封闭的群是这个群中任何一个方程的解都包含在这个群里。例如,如果这是一个包含 \(\{0,1,2\}\) 的循环群 \(\mathbb Z_2\) ,那么等式 \(x^2 = 1\) 的结果是 \(1\) ,这在群 \(\{0,1,2\}\) 中。然而,如果我们可以找到一个方程,它的解不在 \(\mathbb Z_2\) 中,但在实数 \(\mathbb R\) 中,那么这个群非闭。事实上,这很容易,等式 \(x/3=1\) 的结果是 \(3\) ,而 \(3\) 不在 \(\mathbb Z_2\) 中。
(参考:< Algebraically closed group >)
预告¶
实际上我们已经涵盖了大部分基本的数学知识,以便我们开始使用简单复形来计算拓扑特征,这就是我们下次要做的。
参考文献(网站)¶
参考文献(学术刊物)¶
-
Basher, M. (2012). On the Folding of Finite Topological Space. International Mathematical Forum, 7(15), 745–752. Retrieved from http://www.m-hikari.com/imf/imf-2012/13-16-2012/basherIMF13-16-2012.pdf
-
Day, M. (2012). Notes on Cayley Graphs for Math 5123 Cayley graphs, 1–6.
-
Doktorova, M. (2012). CONSTRUCTING SIMPLICIAL COMPLEXES OVER by, (June).
-
Edelsbrunner, H. (2006). IV.1 Homology. Computational Topology, 81–87. Retrieved from Computational Topology
-
Erickson, J. (1908). Homology. Computational Topology, 1–11.
-
Evan Chen. (2016). An Infinitely Large Napkin.
-
Grigor’yan, A., Muranov, Y. V., & Yau, S. T. (2014). Graphs associated with simplicial complexes. Homology, Homotopy and Applications, 16(1), 295–311. HHA 16 (2014) No. 1 Article 16
-
Kaczynski, T., Mischaikow, K., & Mrozek, M. (2003). Computing homology. Homology, Homotopy and Applications, 5(2), 233–256. HHA 5 (2003) No. 2 Article 8
-
Kerber, M. (2016). Persistent Homology – State of the art and challenges 1 Motivation for multi-scale topology. Internat. Math. Nachrichten Nr, 231(231), 15–33.
-
Khoury, M. (n.d.). Lecture 6 : Introduction to Simplicial Homology Topics in Computational Topology : An Algorithmic View, 1–6.
-
Kraft, R. (2016). Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology.
-
Lakshmivarahan, S., & Sivakumar, L. (2016). Cayley Graphs, (1), 1–9.
-
Liu, X., Xie, Z., & Yi, D. (2012). A fast algorithm for constructing topological structure in large data. Homology, Homotopy and Applications, 14(1), 221–238. HHA 14 (2012) No. 1 Article 11
-
Naik, V. (2006). Group theory : a first journey, 1–21.
-
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. (2015). A roadmap for the computation of persistent homology. Preprint ArXiv, (June), 17. Retrieved from [1506.08903] A roadmap for the computation of persistent homology
-
Semester, A. (2017). § 4 . Simplicial Complexes and Simplicial Homology, 1–13.
-
Singh, G. (2007). Algorithms for Topological Analysis of Data, (November).
-
Zomorodian, A. (2009). Computational Topology Notes. Advances in Discrete and Computational Geometry, 2, 109–143. Retrieved from CiteSeerX - Computational Topology
-
Zomorodian, A. (2010). Fast construction of the Vietoris-Rips complex. Computers and Graphics (Pergamon), 34(3), 263–271. Redirecting
-
Symmetry and Group Theory 1. (2016), 1–18. Redirecting