Skip to content

五（上）

本文由 简悦 SimpRead 转码， 原文地址 zhuanlan.zhihu.com

在这一部分中，我们终于要利用我们所学的所有知识来计算持续同调群，并绘制持续性图来图像化地总结信息。

让我们来总结一下我们目前所知道的。

  1. 如何使用任意距离参数 \(\epsilon\) 的点云数据生成一个单纯复形。
  2. 如何计算单纯复形的同调群
  3. 如何计算单纯复形的连通数

从我们知道的到单纯同调的跨度从概念上说很小。我们只需要计算连续改变的 \(\epsilon: 0 \rightarrow \infty\) 生成的一系列单纯复形集合的连通数。然后，我们可以看到哪些拓扑特性持续时间明显比其他的长，说明它们是信号而不是噪声。

注意：我忽略了 “持续时间” 的客观定义，因为这是一个统计问题，超出了这个阐述的范围。对于我们在这里所考虑的所有例子，很明显，只需要目测就知道它们持续时间的长短。

不幸的是，概念上的跨度虽然很小，但技术上的跨度却很大。特别是如果我们还想问最初的数据集中是那些数据点发出了这些持续性的拓扑信号，从而构成这个数据集空间特定的拓扑特性。

让我们重新回顾一下我们在构建圆圈而 (带有一些随机性) 采样的数据点以及构建简单复形的代码。

import numpy as np
import matplotlib.pyplot as plt

n = 30 #number of points to generate

#generate space of parameter
theta = np.linspace(0, 2.0*np.pi, n) 

a, b, r = 0.0, 0.0, 5.0

x = a + r*np.cos(theta)
y = b + r*np.sin(theta)

#code to plot the circle for visualization
plt.plot(x, y)
plt.show()


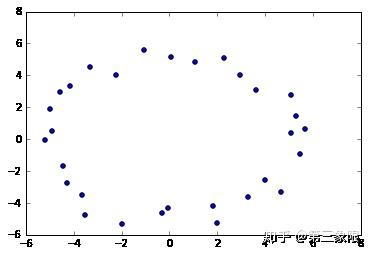
x2 = np.random.uniform(-0.75,0.75,n) + x #add some "jitteriness" to the points
y2 = np.random.uniform(-0.75,0.75,n) + y
fig, ax = plt.subplots()
ax.scatter(x2,y2)
plt.show()


newData = np.array(list(zip(x2,y2)))
import SimplicialComplex

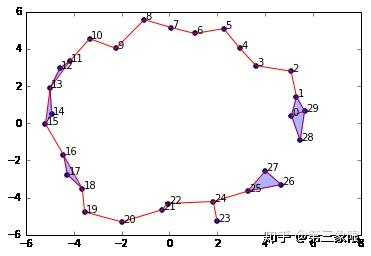
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=3.0) #Notice the epsilon parameter is 3.0
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)

如你所见，设置 \(\epsilon = 3.0\) 生成一个还不错的单纯复形，它捕获了原始数据的 1 维 “孔”。

然而，让我们改变 \(\epsilon\) ，看看它会怎么改变我们的复形。

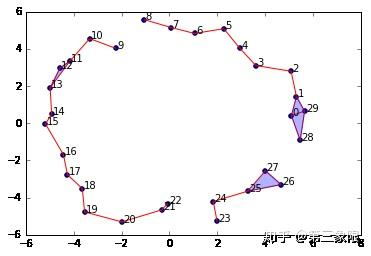
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=2.0)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)

我们把 \(\epsilon\) 减到 \(2.0\) ，现在我们的圆有了一个 “破口”。如果我们计算这个复形的同调和连通数，我们将不再有一个 \(1\) 维圈圈。我们将只看到一个连接的组件。

我们再把它减到 \(1.9\) 。

newData = np.array(list(zip(x2,y2)))
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=1.9)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)

现在我们有三个连接的组件，复形中没有圈圈 / 孔洞。OK，让我们试试把\(\epsilon\) 加到\(4.0\)。

newData = np.array(list(zip(x2,y2)))
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=4.0)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)

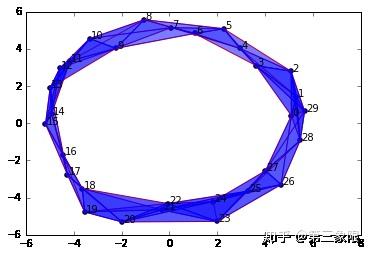
和把半径参数 \(\epsilon\) 减降 \(1\) 个单位不同，把 \(\epsilon\) 加到 \(4.0\) ，我们没有改变我们的同调群。我们仍然有一个连接的组件和一个 \(1\) 维的圆环。

让我们直接把 \(\epsilon\) 加到 \(7.0\) 。

graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=7.0)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)

好吧，尽管我们已经给原来的 \(3.0\) 加了 \(4\) 个单位量，但我仍然得到一个同样拓扑特性的复形：一个连接的组件和一个 \(1\) 维的圆环。

这是在持续同调中持续的拓扑量化分析所能获得的洞见。由于这些观测到的特征在大范围的 \(\epsilon\) 中是持续存在的，因此它们很可能是底层数据的真实特征，而不是噪音。

我们可以用两种主要的可视化来展示我们的发现：条形码图和持续性图。下面是上面例子的条形码图：

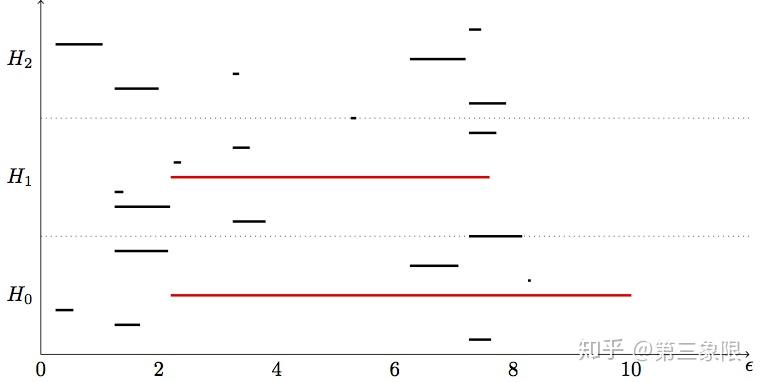
注意：我通过”分段式 “的方式完成了条码图，也就是说，它不是精确计算的条码图。我在噪音中标亮了“真正” 的拓扑特征。 \(H_0, H_1, H_2\) 指的是各维度的同调群和连通数的情况。

重要的是，可能有两种不同的真实拓扑特征在不同的尺度上存在，因此只用一个持续同调来捕捉，它可能会被单一尺度下的单纯复形忽略。例如，如果数据样子是大圆旁边有小圆，可能 \(\epsilon\) 较小时，只有小圆会被连接，产生一个 \(1\) 维孔洞，然后在 \(\epsilon\) 较大时，大圈会被连接，而小圈会被 “填满”。所以没有适合的 \(\epsilon\) 值能够显示出两个圈。

滤流

原来有一种相对直接的方法来扩展我们之前计算边界矩阵的连通数的工作，以及处理不断膨胀的持续同调的集合。

我们定义 复形滤流 是由不断增加的比例参数 \(\epsilon\) 生成的单纯复形的序列。

用滤流的方式来处理持续性计算的精要在于，与其构建多个不同的 \(\epsilon\) 参数的单纯复形，然后把它们组合成一个序列，不如在我们的数据上用一个大（最大）的 \(\epsilon\) 值构建一个简单复形。然后我们会记录所有点两两之间的距离 (我们已经用我们写的算法做过)，所以我们知道什么 \(\epsilon\) 值会使每对点形成边。因此在各个 \(\epsilon\) 值中隐藏着的所有单纯复形构成了一个连贯的滤流（或者说，一系列嵌套的复形）。

下面有一个非常简单的例子：

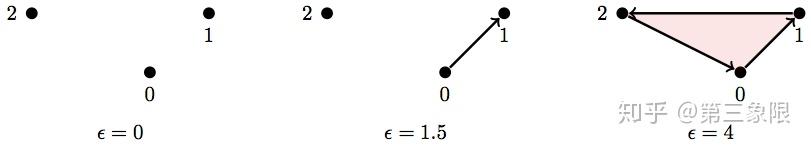
所以如果我们取最大值， \(\epsilon=4\) ，我们的单纯复形是：

\(\\ S = \text{ { {0}, {1}, {2}, {0,1}, {2,0}, {1,2}, {0,1,2} } }\)

但如果我们追踪点与点之间的距离（即所有边的长度 / 比重），那么就会得到足够的信息来刻画需要的滤流。

下面是该单纯复形（竖线表示比重 / 长度）每条边（ \(1\) 维）的比重（长度）：

\(\\ |{0,1}| = 1.4 \\ |{2,0}| = 2.2 \\ |{1,2}| = 3\)

而这是我们用这些信息构建滤流的方法：

\[\\S_0 \subseteq S_1 \subseteq S_2 \\ S_0 = \text{ { {0}, {1}, {2} } } \\ S_1 = \text{ { {0}, {1}, {2}, {0,1} } } \\ S_2 = \text{ { {0}, {1}, {2}, {0,1}, {2,0}, {1,2}, {0,1,2} } } \\\]

基本上，当它最长的边出现时，子复形中每一个单形的域流都将出现。所以 \(2\) 维复形 \(\{0,1,2\}\) 只会在边 \(\{1,2\}\) 出现的时候出现，因为那条边是最长的。

为了让它变成滤流，从而用在我们（将来）的算法中，它需要有 全序。全序 是在滤流中单形根据 “小于” 关系（即任意两个单形的 “值” 都不等）的排序。最常见的关于集合全序的例子来自自然数集 \(\{0,1,2,3,4,...\}\) ，因为没有两个数是相等的，我们总是可以说一个数比另一个数大或者小。

我们怎么确定单形在滤流中的 “值”（滤值）（从而确定域流的顺序）呢？我之前就说过了。单形的滤值部分取决于最长边的长度。但有时两种不同的单形的最长边是一样长的，所此我们必须定义一种规则来确定单形的值 (顺序)。

对于任意两个单形 \(\sigma_1, \sigma_2\) ：

  1. \(0\) 维单形必须比 \(1\) 维单形少， \(1\) 维单形必须比 \(2\) 维单形少，以此类推。这意味着单形的任意面（即 \(f \subset \sigma\) ）自动小于（按顺序之前）单形。即如果 \(dim(\sigma_1) < dim(\sigma_2) \implies \sigma_1 < \sigma_2\) （ \(dim =\) 维度，符号 \(\implies\) 意思是 “意味着”）

  2. 如果 \(\sigma_1, \sigma_2\) 的维度相等（因此彼此都不是另一个的面），那么每个单形的值由它最长（比重最大）的 \(1\) 维单形（边）决定。在我们上面的例子中， \(\{0,1\} \lt \{2,0\} \lt \{1,2\}\) 取决于它们各自的比重。为了比较高维单形，你仍旧只需要通过对比它们最大边的值比较它们。即如果 \(dim(\sigma_1) = dim(\sigma_2)\) ，那么 \(max\_edge(\sigma_1) < max\_edge(\sigma_2) \implies \sigma_1 < \sigma_2\) 。

  3. 如果 \(\sigma_1, \sigma_2\) 具有相同维度，而它们的最长边也相等（即它们最长边在相同 \(\epsilon\) 值进入域流），那么 \(max\_vertex(\sigma_1) < max\_vertex(\sigma_2) \implies \sigma_1 < \sigma_2\) 。什么是最大结点？我们只需要任意给结点排序，即使它们同时出现。

顺便说一下，我们刚才讨论了全序。这个想法的推论是偏序，我们在一些但并非所有元素之间定义了 “少于” 关系，而另一些元素可能和其他相等。

记得第三章时我们讲过如何通过设置列来表示 \(n\) 维链群中 n 维单形，以及用行表示 （）\(（n-1）\) 链群中的 （）\(（n-1）\) 维单形，来设置边界矩阵？我们可以用下面的方法来扩展这个过程以此通过整个域流复形计算连通数。

让我们用上面的域流：

\[\\S_0 \subseteq S_1 \subseteq S_2 \\ S_0 = \text{ [ {0}, {1}, {2} } ] \\ S_1 = \text{ [ {0}, {1}, {2}, {0,1} ] } \\ S_2 = S = \text{ [ {0}, {1}, {2}, {0,1}, {2,0}, {1,2}, {0,1,2} ] } \\\]

注意我已经用方括号表示在每个子复形按顺序（我在单形的集合中加入了全序）的域流中的单形。

因此，我们将以与我们之前维每个同源群建立各自的边界矩阵相同的方式为整个域流建立一个边界矩阵。

然后，像之前一样，我们让每个单元 \([i,j]=1\) 如果 \(\sigma_i\) 是 \(\sigma_j\) 的面。其他单元为 \(0\) 。

这是上面的域流中它的样子:

\(\\\partial_{filtration} = \begin{array}{c|lcr} \partial & \{0\} & \{1\} & \{2\} & \{0,1\} & \{2,0\} & \{1,2\} & \{0,1,2\} \\ \hline \{0\} & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ \{1\} & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ \{2\} & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ \{0,1\} & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \{2,0\} & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \{1,2\} & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \{0,1,2\} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\)

正如上面，我们将用一个算法来改变这个矩阵的形式。然而，不像从前，我们将这个边界矩阵转换为 Smith 标准型，我们现在要把它变成另一种叫列阶梯型。这个转换过程叫做矩阵化减（Matrix Reduction），这意味着我们把它简化成一个简单的形式。

矩阵化减

现在，我要为我在上一篇文章中犯下的错误道歉，因为我从来没有解释过为什么要把边界矩阵转换为 Smith 标准型，我只说了怎么做。

我们之前的的边界矩阵给了我们一个从 \(n\) 维链群到 （）\(（n-1）\) 维链群的线性映射。我们可以用 \(n\) 链中任意元素乘以边界矩阵，结果得到 （）\(（n-1）\) 链中对应（映射）的元素。当我们将矩阵简化为 Smith 标准型时，我们改变了边界矩阵，这样我们就不能再乘以它来映射元素了。我们所做的实际上是在边界矩阵上应用另一个线性映射，结果是 Smith 标准型。

更正式地讲，矩阵 \(A\) 的 Smith 标准型 \(R\) 是矩阵乘积： \(R=SAT\) ，其中 \(S,T\) 是其它矩阵。因此我们有构成 \(R\) 的线性映射，以及我们原则上可以分解 \(R\) 进入组成它单独的线性映射中。

因此，减少到 Smith 标准型的算法本质上是找到另外两个矩阵 \(S,T\) ，使得 \(SAT\) 生成一个沿着对角线以 \(1\) 作为元组成的矩阵。

但为什么我们要这么做？记住，矩阵作为线性映射意味着它将一个向量空间映射到另一个向量空间。如果我们有矩阵 \(M: V_1 \rightarrow V_2\) ，那么它映射基向量 \(V_1\) 到基向量 \(S_2\) 。所以当我们减化矩阵，本质上，我们重新定义了每个向量空间中的基向量。正是这样，Smith 标准型找到了形成环和边界的基础。有许多不同类型的减化矩阵的形式，它们拥有有用的解释和性质。我不打算再讲数学了，我只是想稍微解释一下我们正在做的矩阵化减。

当我们通过算法把滤流边界矩阵变成列阶梯型，它告诉我们，在每个维度上有特定的拓扑特征是在域流的不同阶段形成还是 “消亡”（通过被归入更显著的特征）（即增加 \(\epsilon\) 的值，通过全序在域流中表示）。因此，一旦我们减化了边界矩阵，我们所需要做的就是在特性形成或消亡的时候将信息作为间隔读取，然后我们可以将这些间隔绘制成条形码图。

列阶梯型 \(C\) 同样是线性映射的组成，正如 \(C=VB\) ，其中 \(V\) 是一些使组成有效的矩阵， \(B\) 是滤流边界矩阵。事实上一旦我们减化了 \(B\) ，我们仍将保持 \(V\) 的副本，因为 \(V\) 记录了需要的信息，从而让我们知道那些数据点构成了该数据点云空间里让我们感兴趣的拓扑特征。

将矩阵转化成列阶梯型的普适性方法是高斯消去法的一种：

for j = 1 to n
    while there exists i < j with low(i) = low(j) 
        add column i to column j
    end while
end for

当中的函数 low 输入 \(j\) 列返回最低的 \(1\) 的行索引。举个例子，如果我们有矩阵的一行：

\(j = \begin{pmatrix} 1 \\ 0 \\1 \\1 \\ 0 \\0 \\0 \end{pmatrix}\)

那么 low( \(j\) ) \(=3\) （索引从 \(0\) 开始）因为列中最低的 \(1\) 在第 \(4\) 行（索引为 \(3\) ）。

基本上，算法从左到右扫描矩阵中的每一列，所以如果我们现在在 \(j\) 列，算法会找所有在 \(j\) 列前的 \(i\) 列使得 low( \(i\) ) \(==\) low( \(j\) )，而如果它找到了这样一列 \(i\) ，它会把那一列加到 \(j\) 中。我们还会在另一个矩阵中记录每次我们把一列加到另一列的过程。如果某一列全是 \(0\) ，那么 low( \(j\)) \(=-1\) （代表未定义）。

让我们用上面的边界矩阵手动计算，尝试这个算法。我已经删除了列 / 行标签，以便更简洁：

\(\\\partial_{filtration} = \begin{Bmatrix} 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{Bmatrix}\)

所以记住，列是 \(j\) ，行是 \(i\) 。我们从左到右扫描。前三列全是 \(0\) ，所以 low( \(j\) ) 没有被定义，我们什么都不用做。而当我们到了第四列（\(j=3\) ），因为之前所有列都是 \(0\) ，所以我们还是什么都不做。当我们到第五列（ \(j=4\) ），那么 low( \(4\) ) \(=2\) 而 low( \(3\) ) \(=1\) ，因为 low( \(4\))!=low( \(3\) )，我们不用做什么。而到了第六列（ \(j=5\) ），存在一列 \(i < j\) （在这个情况下，列 \(4<5\) ），而且 low( \(4\) )=low( \(5\) )。所以我们把 \(5\) 列加到 \(6\) 列。因为这是二进制列， \(1+1=0\) 。把 \(5\) 列加到 \(6\) 列的结果如下：

\(\\ \partial_{filtration} = \begin{Bmatrix} 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{Bmatrix}\)

现在我们继续到最后，最后一列的最低的 \(1\) ，只有那一列，所以我们什么都不做。现在我们再从左边开始。我们到了第 \(6\) 列，发现第 \(4\) 列最低的 \(1\) 和它一样，low( \(3\) )=low( \(5\) )，所以我们把第 \(4\) 列加到第 \(6\) 列，结果如下：

\(\\\partial_{filtration} = \begin{Bmatrix} 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{Bmatrix}\)

看，我们现在有了一个全为 \(0\) 的新列！而这是什么意思？它意味着列是新的拓扑特征。它要么表示连通的分量，要么表示某些 \(n\) 维圈。在这中情况下，他表示一个 \(1\) 维圈，这个圈由三个 \(1\) 维单形组成。

注意到现在矩阵被完全还原到列阶梯型，因为左右最低的 \(1\) 都不在同一行，所以我们的算法能满足需求。现在，边界矩阵被减化了，不再是每一列和一行表示滤流中唯一一个单形的情况。因为我们已经将各列加在一起，所以每一列都可以表示滤流中多个单形。在本例中，我们只把列加起来两次，而且两次加的都是第 \(6\) 列（ \(j=5\) ），所以第 \(6\) 列表示第 \(5\) 列和第 \(4\) 列的单形（恰好是 \(\{0,1\}\) 和 \(\{2,0\}\) ）。所以第 \(6\) 列是单形的群： \(\text{ {0,1}, {2,0}, {1,2} }\) ，如果你回头看这个单形的图形表示，那些 \(1\) 维单形组成了一个 1 维循环（尽管立即被 \(2\) 维单形 \(\{0,1,2\}\) 消除掉了）。

保持对算法的跟踪记录是很重要的，这样我们就能在算法完成时找出每一列代表什么。我们通过建立另一个我称之为 记忆矩阵 的矩阵来做这个。它开始只是与边界矩阵维数相同的单位矩阵。

\(\\M_{memory} = \begin{Bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{Bmatrix}\)

但每次我在我们的还原算法中把 \(i\) 列加到 \(j\) 列，我们就要将 \(1\) 放入单元 \([i,j]\) ，在记忆矩阵中记录这一变化。所以在我们的例子中，我们记录了添加列 \(4\) 和 \(5\) 到第 \(6\) 列的事件。因为在我们的记忆矩阵中，我们让单元 \([3,5]\) 和 \([4,5]\) 等于 \(1\) 。具体如下：

\(\\M_{memory} = \begin{Bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{Bmatrix}\)

一旦算法运行完毕，我们总可以参考这个记忆矩阵来回忆算法实际做了什么，并计算出减少边界矩阵的列。

让我们回顾一下我们降低 (列阶梯型) 边界矩阵的滤流：

\(\\\partial_{reduced} = \begin{Bmatrix} 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{Bmatrix}\)

为了记录拓扑特征的形成和消亡间隔，我们只需扫描从左到右的每一列。如果 \(j\) 列全是 \(0\) （即 low( \(j\) ) \(=-1\) ）那么我们将这记为新特征的形成（不管 \(j\) 代表什么，可能是一个单形，可能是一组单形）。

否则，如果一列不是所有的 \(0\) ，而是有一些 \(1\) ，那么我们就会说，在 \(j\) 中等于 low( \(j\) ) 的列，因此是该特性的区间的端点。

在我们的例子中，所有三个顶点 (前三列) 都是生成的新特性(它们的列都是 \(0\) ，low( \(j\) ) \(=-1\) )，因此我们记录 \(3\) 个新的间隔，起始点是它们的列索引。因为我们从左到右进行顺序扫描，我们还不知道这些特征何时会消失，所以我们只是暂时将端点设置为 \(-1\) ，以表示结束或无限。这是前三段：

#Remember the start and end points are column indices
[0,-1], [1,-1], [2,-1]

然后我们继续从左到右扫描，到了第 \(4\) 列 ( \(j=3\) )，我们计算 low( \(3\) )= \(1\) 。所以这意味着在 \(j=1\) (第 \(2\) 列) 中生成的特性在 \(j=3\) 的时候消失了。现在我们可以返回并更新这个间隔的暂定终点，我们的更新间隔为：

#updating intervals...
[0,-1], [1,3], [2,-1]

我们继续这个过程直到最后一列，我们得到所有的间隔：

#The final set of intervals
[0,-1], [1,3], [2,4], [5,6]

前三个特性是 \(0\) 维单形，因为它们是 \(0\) 维度，它们代表了域流的连接分量。第 \(4\) 个特征是 \(1\) 维循环，因为它的间隔指数指的是 \(1\) 维单形群。

信不信由你，我们刚刚完成了持续同调。这就是它的全部。一旦我们有时间间隔，我们需要做的就是用条形码图画出它们。我们应该通过回到我们在边缘权重的集合，在这些 \(\epsilon\) 值的区间内转换开始 / 结束点，并分配 \(\epsilon\) 值给每个单形。下面是条形码图：

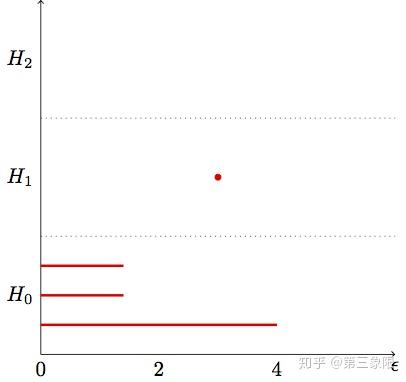
我在 \(H_1\) 群画了一个点来表示 \(1\) 维循环形成并马上在同一点消亡（因为它一形成就有 \(2\) 维循环归并它了）。大多数真正的条码图都不会产生这些点。我们并不关心这些短暂的特性。

注意到现在在 \(H_0\) 中有一条 “横杠” 明显比其他两条长。这表明我们的数据只有 \(1\) 个连接的组件。群 \(H_1,H_2\) 没有任何一根 “横杠”，所以数据没有孔洞 / 循环。当然，有了更真实的数据集，我们也会发现一些环。

由于知乎开始限制每篇文章的字数，第五章需要分上，下两部分才能完整发布出来。在这里的上半部我们完成了持续同调理论部分的介绍，同时附上所有引用的网络资料和文献的链接。在下半部分，主要完成剩下的代码方面的实现。

参考文献（网站）

  1. Loading...

  2. http://www.math.uiuc.edu/~r-ash/Algebra/Chapter4.pdf

  3. Group (mathematics)

  4. Homology Theory — A Primer

  5. http://suess.sdf-eu.org/website/lang/de/algtop/notes4.pdf

  6. Evan Chen • Napkin

参考文献（学术刊物）

  1. Basher, M. (2012). On the Folding of Finite Topological Space. International Mathematical Forum, 7(15), 745–752. Retrieved from http://www.m-hikari.com/imf/imf-2012/13-16-2012/basherIMF13-16-2012.pdf

  2. Day, M. (2012). Notes on Cayley Graphs for Math 5123 Cayley graphs, 1–6.

  3. Doktorova, M. (2012). CONSTRUCTING SIMPLICIAL COMPLEXES OVER by, (June).

  4. Edelsbrunner, H. (2006). IV.1 Homology. Computational Topology, 81–87. Retrieved from Computational Topology

  5. Erickson, J. (1908). Homology. Computational Topology, 1–11.

  6. Evan Chen. (2016). An Infinitely Large Napkin.

  7. Grigor’yan, A., Muranov, Y. V., & Yau, S. T. (2014). Graphs associated with simplicial complexes. Homology, Homotopy and Applications, 16(1), 295–311. HHA 16 (2014) No. 1 Article 16

  8. Kaczynski, T., Mischaikow, K., & Mrozek, M. (2003). Computing homology. Homology, Homotopy and Applications, 5(2), 233–256. HHA 5 (2003) No. 2 Article 8

  9. Kerber, M. (2016). Persistent Homology – State of the art and challenges 1 Motivation for multi-scale topology. Internat. Math. Nachrichten Nr, 231(231), 15–33.

  10. Khoury, M. (n.d.). Lecture 6 : Introduction to Simplicial Homology Topics in Computational Topology : An Algorithmic View, 1–6.

  11. Kraft, R. (2016). Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology.

  12. Lakshmivarahan, S., & Sivakumar, L. (2016). Cayley Graphs, (1), 1–9.

  13. Liu, X., Xie, Z., & Yi, D. (2012). A fast algorithm for constructing topological structure in large data. Homology, Homotopy and Applications, 14(1), 221–238. HHA 14 (2012) No. 1 Article 11

  14. Naik, V. (2006). Group theory : a first journey, 1–21.

  15. Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. (2015). A roadmap for the computation of persistent homology. Preprint ArXiv, (June), 17. Retrieved from [1506.08903] A roadmap for the computation of persistent homology

  16. Semester, A. (2017). § 4 . Simplicial Complexes and Simplicial Homology, 1–13.

  17. Singh, G. (2007). Algorithms for Topological Analysis of Data, (November).

  18. Zomorodian, A. (2009). Computational Topology Notes. Advances in Discrete and Computational Geometry, 2, 109–143. Retrieved from CiteSeerX - Computational Topology

  19. Zomorodian, A. (2010). Fast construction of the Vietoris-Rips complex. Computers and Graphics (Pergamon), 34(3), 263–271. Redirecting

  20. Symmetry and Group Theory 1. (2016), 1–18. Redirecting