一

本文由 简悦 SimpRead 转码， 原文地址 zhuanlan.zhihu.com

申明

在流形科技一早就想用中文比较系统和严谨的介绍一下 TDA，而在网上「偶然」发现 Δ ℚuantitative √ourney 的博客，如此系统详尽的介绍了 TDA 的核心概念：持续同调。更漂亮的是，所有的概念都有可执行的代码实现！立即联系了博主，Brendon，征得他同意后，和伙伴翻译成中文，现在发布出来，以下均是 Topological Data Analysis - Persistent Homology 在 Δ ℚuantitative √ourney 的中文版本。

引言

我发现拓扑数据分析（TDA）成为了数据分析中一个最令人兴奋的发展方向，因此，我想尽我所能地去传播相关知识。那么，这到底是什么呢？TDA 主要有两个方向：持续同调和 mapper （译者注：Ayasdi 和其他一些 TDA 商业化－包括湃势科技，所依托的 TDA 可视化算法，概念上运用了类似持续同调的思维来构建，故称 TDA 以持续同调为跟本是无误的）。两种都很有用，也能用作互相补充。在接下来的帖子中，我们将讨论持续同调。一般而言，TDA 和数学紧密相关，所以在学习它之前，我们需要许多的数学铺垫。因此，如同 TDA 一样，我们将复习高等数学中的许多内容，所以如果你对 TDA 没有兴趣，但想要学习拓扑学，群论，线性代数，图论和抽象代数，相信你也能在那一方面有所收获。当然，我不会像教科书那样详尽地介绍这些数学问题，但我希望如果你明白我在说什么，找本书来读读将更有收获。

什么是持续同调，为什么我们关注它？

想象一下，一组 100 x 900 的典型数据集，以 Excel 文件的形式储存，它的列（100）是各种参数，行（900）是独立的数据点。如果我们将行看作数据，那么这将是 100 维的数据点。显然在这个 3 维宇宙中，我们没有办法去描述数据的全貌。当然，我们有很多办法将高维数据降维到我们能观察到的低维空间。通常我们希望能 “看见” 数据，这样我们就轻易地识别模式，尤其是群集。这些可视化方法中，最有名的莫过于主成分分析（PCA）。但所有的方法都会或多或少地丢失一些有潜在价值的数据，因为如果我们想用 PCA 将 100 维的数据浓缩到 2 维图像中，我们一定会丢失信息。

持续同调（PH）为我们提供了一个寻找不需要降维就能精要的刻画数据全貌的方法。PH 让我们把数据放在原始的高维空间中，并告诉我们这些数据里面有多少个群集，多少个环结构，而这都不需要我们去切实将这些数据 “可视化”。

举个例子，假如有个生物学家在研究一些细胞中的基因。她用某种工具去测量 900 个不同细胞的 100 个不同基因不同水平的表达。她关注一些可能在细胞的分类上扮演着重要角色的基因。作为一个先进的生物学家，她利用持续同调去分析她的数据，而 PH 告诉她数据有一个明显的周期，于是她进一步分析发现并可以确信她一百个基因的某个子集有一个周期性的表达模式。

拓扑学领域在数学空间性质的研究中主要关注的是点与点之间的关系，不像几何学，还会去关注精确的距离和角度。因此，PH 让我们以可靠的，不掺杂任何数据挖掘和加工扭曲的方式提出关于我们数据的拓扑性问题，持续同调的传统输出是一个 “条形码” 图，看起来像这样：

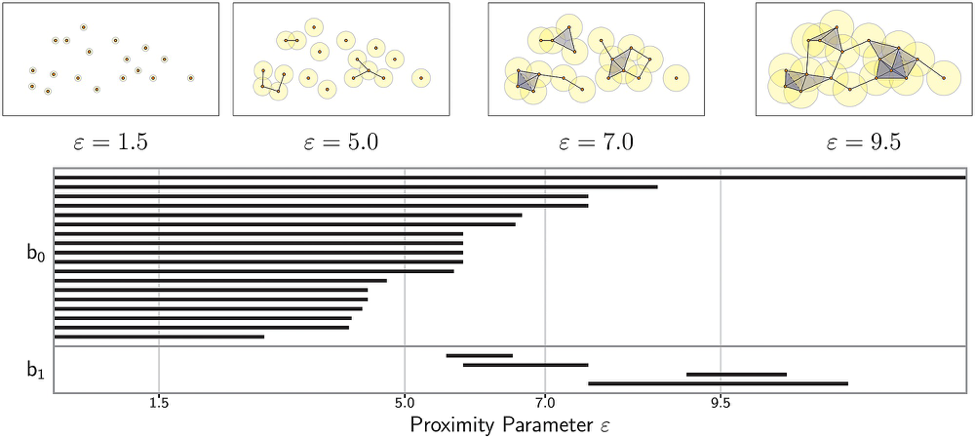
这张图用一种简洁可视的方式编译了所有我们感兴趣的拓扑学特征。

目标受众

像往常一样，我的目标受众是那些和我一样的人。我是一个对 TDA 感兴趣的程序员。我在大学里主修神经科学，因此高中以后，我就再没有系统的数学训练了。所有东西都是自学的，如果你有数学方面的学位，那这帖子不是写给你的，但你可以看看我大量的引用列表。

数学基础

我经常试图让我的帖子被一些有编程背景和数学基础知识的普通人看懂，因此我作了很多假设。我假设您对以下内容有基本的了解：

• 高中代数
• 集合论
• Python 和 Numpy

但我会尝试尽量多地解释。如果你能跟上我以前的帖子，那你也能跟上这篇。

集合论复习

我们将快速复习集合论的基础，但我假设你对集合论的背景知识已有必要的了解，这只是一个对我们需要用到的部分的复习引导。

集合是一个抽象的数学结构，它是一些无序的抽象对象组成的整体，通常用花括号表示，例如，集合 \(S=\{a, b, c\}\) 。集合中包含的对象称为其元素。若 \(a\) 是集合 \(S\) 的元素，则称 \(a\) 属于 \(S\) ，记作 \(a\in S\) 。若 \(d\) 不是集合 \(S\) 的元素，则称 \(d\) 不属于 \(S\) ，记为 \(d\not\in S\) 。直观点说，你可以把一个集合看成一个盒子或容器，你可以把各种各样的东西放入盒子里（包括其他盒子）。

设 \(S,T\) 是两个集合，如果 \(S\) 的所有元素都属于 \(T\) ，即 \(x\in S\Longrightarrow x\in T\) ，则称 \(S\) 是 \(T\) 的子集，记为 \(S\subseteq T\) 。显然，对任何集合 \(S\) ，空集和集合本身都是 \(S\) 的子集，即 \(S\subseteq S\) ， \(\emptyset \subseteq S\) 。其中，符号 \(\subseteq\) 读作包含于，表示该符号左边的集合中的元素全部是该符号右边集合的元素。如果 \(S\) 是 \(T\) 的一个子集，即 \(S \subseteq T\) ，但在 \(T\) 中存在至少一个元素 \(x\) 不属于 \(S\) ，即 \(S\subsetneq T\) ，则称 \(S\) 是 \(T\) 的一个真子集。

符号 \(\forall\) 代表 ” 任意 “，符号 \(\exists\) 代表存在。比如，我们可以说任意 \(x\) 属于 \(S\) ，即 \(\forall x\in S\) ，我们也可以说当 \(x=a\) 时，存在 \(x\) 属于 \(S\) ，即 \(\exists x\in S, x=a\) 。

符号 \(\lor\) 代表 “或者”，符号 \(\land\) 代表 “并且”，例如，集合 \(S_1=\{a, b, c\}\) ，集合 \(S_2=\{d, e\}\) ，那么 \(a\in S_1\land a\in S_2\) 为假命题，因为 \(a\) 不属于 \(S_2\) ，但是 \(a\in S_1 \lor a\in S_2\) 为真命题，因为 \(a\) 属于两个集合中的一个。

由所有属于集合 \(S_1\) 或属于集合 \(S_2\) 的元素所组成的集合，记作 \(S1\cup S2\) （或 \(S_2\cup S_1\) )，读作 “ \(S_1\) 并 \(S_2\) ”（或 “ \(S_2\) 并 \(S_1\) ”），假如 \(S_1=\{a, b, c\}\) ， \(S_2=\{d, e\}\) ，则 \(S_1\cup S_2=\{a, b, c, d, e\}\)。

我们可以用集合符号描述这一定义，即 \(S_1\cup S_2=\{x|\forall x\in S_1, \forall x\in S_2\}\) 或 \(S_1\cup S_2=\{x|\forall x\in S_1\lor \forall x\in S_2\}\) 。竖线 \(|\) 前表示构成该集合的元素，而在竖线之后的部分描述了这些元素必须满足的条件。

由属于 \(S_1\) 且属于 \(S_2\) 的相同元素组成的集合，记作 \(S_1\cap S_2\) （或 \(S_2\cap S_1\) ），读作 “ \(S_1\) 交 \(S_2\) ”（或 “ \(S_2\) 交 \(S_1\) ”），即 \(S_1∩S_2=\{x|x\in S_1\land x\in S_2\}\) 。

集合的大小或势表示集合中元素的个数，如 \(S=\{a, b, c\}\) ，那么 \(S\) 的势为 \(3\) ，即 \(|S|=3\) 。

函数是一个集合中的元素与另一个集合之间的关系。我们可以想象一个函数：

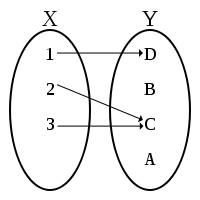
假设集合 \(X=\{1, 2, 3\}\) 和集合 \(Y=\{A, B, C, D\}\) ，那么函数\(f\) 表现出了 \(X\) 中元素到 \(Y\) 中元素的映射。如 \(f(1)=D\) 表示函数 \(f\) 是 \(1\in X\) 到 \(D\in Y\) 的映射。

一个通用的映射或者关系可以是一个集合中的元素映射到另一个集合，然而一个函数只能为每个输入对应一个输出，即域中的每个元素只能映射到上域中的单个元素。

我们通过构建一组新的有序对来定义一个函数。对于两个集合\(X\) 和 \(Y\) ，我们用 \(f: X→Y\) 来表示笛卡尔积 \(X×Y\) 的其中一个子集（即 \(f\subseteq X×Y\) ）。笛卡尔乘积是两个集合中元素之间所有可能的有序对的集合。

例如，上图定义函数 f 的集合是 \(f=\{(1, D), (2, C), (3, C)\}\) 。因此如果我们想知道 \(f(1)\) 的结果，我们只需要找到第一个位置是 1 的有序对，而它的第二个位置元素即为结果（结果是 \(D\) ）。

函数 \(f: X\to Y\) 的像是 \(Y\) 的子集，其元素是被 \(X\) 中的元素映射到的元素。例如，上图中函数的像是 \(\{C, D\}\) ，因为只有这两个元素被 \(X\) 的元素映射。

函数 \(f: X→Y\) 子集 \(K\subseteq Y\) 的原像是集合\(X\) 中映射到 \(K\) 中元素的元素集合。例如，上面所描述的函数的子集 \(K=\{C\}\) 的原像是集合 \(\{2, 3\}\) 。

拓扑学入门

你可能已经猜到了，TDA 涉及拓扑学的数学领域。我不是数学家，但我们又必须有基本的背景，所以我会尽我所能地解释与拓扑学相关的方面，至少在术语和大部分可能的计算方法。

数学通常被分为许多领域的研究，如几何学，拓扑学，线性代数等。每一个领域本质上都是根据研究的数学对象来定义的。线性代数关注的数学对象是向量空间，而拓扑学关注的数学对象是拓扑空间。同时因为集合论被认为是数学的基础，所以所有这些数学对象都是有关于集合形成，以及转换和操作的特定规则的简单集合 (抽象事物的集合)。

定义拓扑空间：

拓扑空间： 是一组有序对 \((X, \tau)\) ，其中 \(X\) 是集合， \(τ\) 是 \(X\) 的子集的集群，他们满足以下性质：
1. 空集和 \(X\) 属于 \(τ\) ，
2. \(τ\) 中任意多个元素的并仍属于 \(τ\) ，
3. \(τ\) 中有限个元素的交仍属于 \(τ\) 。

\(τ\) 的元素称为 开集，集群 \(τ\) 称为 \(X\) 上的一个拓扑。

举个简单的例子，假设集合 \(X=\{a, b, c\}\) ，那么我们有三个不同对象的集合，我们想在这个集合上定义一个拓扑。拓扑 \(τ\) 应该是 X 的子集集合，满足拓扑公理。那么可能拓扑 \(τ\) 应该是 \(\{\{a\}, \{b\}, \{c\}\}\) ，即 \(τ\) 是来自 \(X\) 的单个元素子集的集合。由于空集 \(\emptyset\) 和 全集 \(X\) 属于 \(τ\) ，则 \(τ=\{ϕ, \{a\}, \{b\}, \{c\}, \{a, b, c\}\}\) ，但它不满足以上第 2 点和第 3 点的性质，因此需要修改，为了让 \(τ\) 满足 2，3 性质，我们让 \(τ=\{ϕ, \{a\}, \{a, b, c\}\}\) ，此时 \(τ\) 中任意元素的交集和并集仍属于 \(τ\) ，因此我们可以说在 \(X\) 上有一个有效拓扑，即 \(τ\) 。我知道在这一点上似乎相当学术化，但跟上我，我们最终将会达到利用这些新知识的目的。

紧密性

与其他数学抽象相比，拓扑空间的重要性是什么？一个重要的方面是拓扑空间最终定义了一个定义拓扑的元素之间的紧密关系。在没有定义结构的 “原始” 集合中，如\(Y=\{c, d, e\}\) ，它是抽象对象的集合，就是这样，我们没有更多关于这个集合或者它的元素的描述。但是，一旦我们定义了 \(Y\) 上的一个拓扑，我们就可以问 “元素 \(c\in Y\) 比元素离 \(e\) 更近吗？”

关于数学，一件很有趣的事是，那么多事情是怎么联系在一起的，为什么总有许多定义数学关系的方法，而其中一些比其他更容易理解。到目前为止，我们一直在考虑有限拓扑空间，也就是，我们用来定义拓扑空间的集合 X 有有限个元素。当然，拓扑空间不一定是有限的，我们最终将花费我们大部分时间来考虑无限拓扑空间，例如在实数集合上定义的那些。当我们开始考虑这些类型的空间时，可视化它们往往会更容易，因为我们通常可以绘制图表。你可能已经注意到，所有这些关于开放集定义拓扑空间的抽象概念似乎很难直观地掌握。然而，还是有另一种方法来表示有限拓扑空间，即是用有向图。

图论

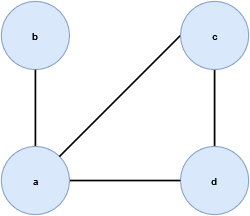
基本图： \(G\) 是顶点 \(V\) 的集合和边 \(E\) 的集合组成的有序二元组，即 \(G=(V, E)\) 。

例如下图， \(G(V, E)\) ，其中 \(V=\{a, b ,c ,d\}\) ， \(E=\{\{a, b\}, \{a, c\}, \{a, d\}, \{c, d\}\}\) 。

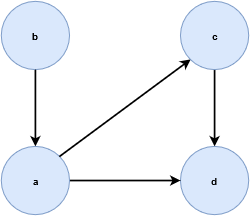
有向图： \(G(V, E)\) 的边集 \(E\) 是顶集 \(V\) 中元素的有序配对。因此，顶点之间的 “连接” 有方向。有序对的第一个顶点是开始，第二个顶点是结束。绘制图形时，边缘是箭头，箭头朝向和接触端点顶点。

例如下图， \(G(V, E)\) ，其中 \(V=\{a, b ,c ,d\}\) ， \(E=\{\{a, b\}, \{a, c\}, \{a, d\}, \{c, d\}\}\) 。

为了完整起见，我想提到一些我们可以在图结构上添加的其他属性。我们已经注意到，图的边可以有方向属性，但是边也可以有一个权值，比如，不同的边可以有不同的权重，这意味着一些连接比其他的更强。当绘制带有加权边的图时，一种描述方法是简单地用更粗的线代表权重更重的边。在数学上，一副具有顶点，边，权重的图会被定义成图 \(G(V, E, ω)\) ，其中 \(ω: E→\mathbb R\) （ \(\omega\) 是一个把 \(E\) 的每条边映射到实数权重的函数）。同样，一个函数可以赋予每个顶点一个权重，它可能描述的是节点 (顶点) 的大小不同反映它们各自的权重。

可视化有限拓扑

事实证明，我们可以在集合 X 中的元素和拓扑 \(τ\) 之间构建一组叫做预序的二元关系。二元关系预序具有自反性（每一个元素和自己有关， \(a \sim a\) ）和传递性（如果 \(a\) 与 \(b\) 有关， \(b\) 与 \(c\) 有关，那么 \(a\) 与 \(c\) 有关，即 \(a∼b∧b∼c⇒a∼c\) ）。预序关系（更确切地说是特殊化预序）有时能由分析 \(X\) 中元素的成对关系所决定。特殊化预序关系一般用 \(≤\) 表示（但它不同于我们认识的小于等于，只是方便书写的符号就那么多，总会有重复的）。

以下是特殊化预序在拓扑空间 \((X, τ)\) 的定义：

特殊化预序： \(x≤y\) ，当且仅当所有包含 \(x\) 的开集都包含 \(y\) 。

记住，开集是拓扑 \(τ\) 的元素。一旦我们确定 \(x≤y\) ， \(\forall x, y\in X\) ，那么我们可以说 \(x\) 是 \(y\) 的特殊化序。这说明 \(y\) 比 \(x\) 更普遍，因为它出现在更多开集中。

例如，为了用我们之前的有限拓扑空间来解释，我们将 \(X=\{a, b, c\}\) 上的拓扑扩大，此时 \(τ=\{\emptyset, \{a\}, \{b\}, \{a, b\}, \{b, c\}, \{a, b, c\}\}\) 。

为了定义此拓扑空间的特殊化预序，我们需要列举拓扑空间上所有点可能的组合，并且用 \(≤\) 标记所有满足预序关系的组合。让我们关注 \((b, c)\) 这一组合，我们想知道 \(c≤b\) 是否为真。根据我们对特殊化预序的定义，如果 \(c≤b\) ，那么所有包含 \(c\) 的开集都包含 \(b\) 。所以当我们列出所有包含 \(c\) 的开集： \(\{b, c\}, \{a, b, c\}\) ，我们发现两个包含 \(c\) 的开集都包含 \(b\) ，因此 \(c≤b\) 为真。重点是，预序关系不代表如果它们互为特殊化序，它们就是相等的，即 \(x≤y∧y≤x⇏x=y\) 。

我将列出所有 X 上对或者错的预序关系，然后我们可以在可视化图中构建拓扑空间。

• \(a≰b\)
• \(a≰c\)
• \(b≰a\)
• \(b≰c\)
• \(c≰a\)
• \(c≤b\)

在 \(X\) 的所有点中，只有一对是真正的预序关系。为了在拓扑空间 \((X, τ)\) 中构建预序关系的有向图，我们简单地将 \(X\) 中的点作为图的顶点，并在有预序关系的两个顶点间画一条有向边，箭头是从特殊化序点指向一般化序点（如果 \(x≤y\) ，则图中会有一条边 \(x\) 指向 \(y\) ）。其他没有关系的点将不连线。这就是例子中 X 的预序作的可视化图。

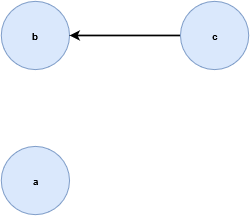
下面是另一个特殊化预序的例子， \(Z=\{a, b, c, d\}\) 是拓扑空间 \(\tau_Z = \{Z, \emptyset, \{b\}, \{a, b\}, \{b, c, d\}\}\) 的一个集合。列出 \(Z\) 的特殊化预序，那么关于此空间特殊化预序的图是这样的。

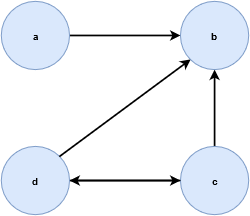
就像你可以选择任何有限的拓扑空间，你可以生成一个拓扑空间上的特殊化预序并建立成图，你也可以用用预序构建的图形来生成它的拓扑。事实上，通过观察图像你可以确定空间的拓扑性质。在这个视角中，你可以将有限拓扑解释为一组带有路径的点。

连通性

我将在这里定义拓扑空间的另一个属性称为连通性，如果你在一张纸上画两个分开的圆，这两个图形代表一个拓扑空间，因为没有线或路径连接两个圆，所以这是一个不连通的拓扑空间。在这种情况下，我们会说空间中有两个分量。直觉告诉我们这个空间有多少个 “整块”。拓扑学中连通性的定义抽象概括了空间中“碎片” 的直观概念。

连通性：如果 \(X\) 不能表示为两个非空互斥的开集的并，我们说拓扑空间 \((X, τ)\) 是连通的。也就是说，如果 \(τ\) 中两个非空互斥的子集的并是 \(X\) ，此拓扑空间是不连通的。

回顾之前的例子， \(X=\{a, b, c\}\) ， \(τ=\{\emptyset, \{a\}, \{b\}, \{a, b\}, \{b, c\}, \{a, b, c\}\}\) ，我们可以确定这个拓扑空间是不连通的，因为两个互斥开集的并集 \(\{a\}\cup \{b, c\}=X\) 。或者，如果我们看着 \(X\) 上用预序生成的图，我们可以看到 \(b\) 和 \(c\) 用一条边连接，而 a 是一个不和其他点连接的点。而关于集合 \(Z\) 的图说明它的空间是连通的，因为所有顶点都以某种方式连接在一起。

有了这些 “纯” 拓扑空间，我们不能再说 “接近” 了，因为我们没有距离的概念了。我们知道 \(b\) 离 \(c\) 更近，但我们不知道有多近。我们所知的只有元素之间的关系，例如，这个元素比这个元素更接近这个元素，等等。

度量空间

你可能已经注意到，我们研究的 “纯” 拓扑空间是相当抽象的。我们将要学习度量空间，这是一种有明确概念距离的拓扑空间，而不仅仅是 “紧密性” 的抽象概念。也就是说，所有的度量空间都是拓扑空间，但不是所有拓扑空间都是度量空间。在度量空间中，许多事情变得容易得多，幸运的是，拓扑数据分析是在处理度量空间而不是 “纯” 拓扑空间。

度量空间：是一对有序对 \((M, d)\) ，其中 \(M\) 是集合，而 \(d\) 是 \(M\) 的度量标准，也就是说函数 \(d：M×M→\mathbb R\) （这定义了函数 \(d\) 将 \(M\) 中元素的每一个有序对映射到实数集 \(\mathbb R\) 的一个元素上），对于任何 \(x, y, z\) 属于 \(M\) ，有
1. \(d(x, y)≥0\) （所有距离都是非负的）
2. \(d(x, y)=0\) 当且仅当 \(x=y\)
3. \(d(x, y)=d(y, x)\) （距离是对称的）
4. \(d(x, z)≤d(x, y)+d(y, z)\) （从 \(x\) 到 \(z\) 的直线距离必不大于经过任何中间点）

这应该相当简单。度量空间只是集合与距离函数的结合，它从集合中获取两个元素并返回这两个元素的度量距离。最让人熟悉的度量空间将是实数轴，集合是实数的集合，而度量是数轴上任意两个数字之间的差值的绝对值（对于任意实数域 \(\mathbb R\) 中的 \(x, y, d=|x-y|\) ）。另一个也很让人熟悉的是 2 维欧几里得空间 \(\mathbb R^2\) ，任意两点 \((x_1, y_1), (x_2, y_2)\) 的距离 \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) 。

欧几里得度量基本定义了一个拓扑空间，其中任何两点之间的最短路径是一条直线。但是我们可以定义一个不同的度量，所有的点都在球面上，因此只有一条曲线是两点之间的最短路径。然而，我们不应局限于实数。我们可以有一个集合是一堆图片，或者文本块，或者任何类型的数据的矩阵空间，只要你能定义一个函数，它能计算出集合中任意两个元素之间的距离，它就是一个有效的度量空间。

连续性

拓扑学中的一个重要概念是连续性概念。想象一下一个正方形的形状的金板 (或者其他一些柔韧的金属)，你可以通过粉碎边缘将边缘变弯的方法将这个平面变成圆形。在拓扑学中，矩形和圆是等价的拓扑空间，因为你可以进行从矩形到圆形的连续变换。既然拓扑学是关于定义点与点之间紧密联系的，如果你连续地将矩形变为圆形，那么变形前任何两个“闭合” 的点，在变形后依旧是 “闭合” 的。尽管从几何角度看，这些图形并不相同，但这些点之间的紧密联系仍然保持不变（在几何中，你关心的是点之间的实际距离，而不是抽象和相对的紧密性）。

同态： 如果两个拓扑空间之间存在函数 \(f:X→Y\) ，其中 \(X\) 和 \(Y\) 是两个拓扑空间 \((X, τ_X)\) 和 \((Y, τ_Y)\) ，那么它们是同态的，其中 \(f\) 满足以下条件：
1. \(f\) 映射了 \(X\) 到 \(Y\) 一一对应的关系（双射）。
2. \(f\) 是连续的。
3. 反函数 \(f^{-1}\) 是连续的。

连续是什么意思？我们将对它的数学定义进行描述，然后试图找到更为直观的含义。

连续函数： 对于两个拓扑空间 \((X, τ_X)\) 和 \((Y, τ_Y)\) 而言，如果每个元素 \(V\in\tau_Y\) （正如 \(Y\) 的开集）的原像 \(f^{-1}(V)\) 存在于 \(X\) 中，那么函数 \(f\) 是连续的。

这是一个连续函数的等价定义，它在拓扑空间中使用了对特殊化预序的理解。

当且仅当函数 \(f：X→Y\) 是保序的： \(X\) 中 \(x≤y\) 表示 \(Y\) 中 \(f(x)≤f(y)\) ，函数 \(f\) 是连续的。

我们必须记住，函数是集合 \(X\) 中每一个元素到集合 \(Y\) 的映射（是集合 \(X\) 到集合 \(Y\) 的映射，而不是它们的拓扑 \(τ_X\) 到 \(τ_Y\) 的映射）。我们还需要从集合论中回忆原像 (或逆像) 的定义。函数 \(f：X→Y\) 的域是 \(X\) ，而它的上域是 \(Y\) 。 \(f\) 的像是 \(Y\) 的子集，也就是说， \(f\) 的像是 \(\{f(x)|x\in X\}\) 。我们还可以说子集 \(U\in X\) 的像是集合 \(\{ f(x)|x\in U\}\) 。 \(f\) 的原像（或逆像）等于 \(f\) 的域，所以我们只提及 \(Y\) 的子集或者单个元素的原像。

集合 \(B \subseteq Y\) 在 \(f\) 的映射下的原像或者逆像是 \(X\) 的子集， \(f^{-1}(B) = \{ x \in X \mid f(x) \in B\}\)

例子（连续函数）：

让 \(X=\{a, b, c\}\) ，它的拓扑 \(\tau_X = \{\emptyset, \{a\}, X\}\) ； \(Y=\{d\}\) ，它的拓扑 \(\tau_Y = \{\emptyset, Y\}\) 。连续函数 \(f：X→Y\) 如下图描述。

我们可以看到原像 \(f^{-1}(\{d\})=\{a, b, c\}\) 是 \(X\) 的开集，因此函数是连续的。是的，它是一个叫做常数函数的非常不起眼的函数，因为所有 \(X\) 都映射到同一个元素。

单纯形和单纯复形

拓扑数据分析使用了单纯复形，这是一种由叫做单纯形的几何结构组成而成。TDA 使用单纯复形是因为它们可以近似比较复杂的形状，而且它们比它们近似的原始图形在数学和计算上更容易处理。

总之，单纯形是一个三角形到任意维度的泛化。例如，在 2 维中，我们称 2 维单纯形为三角形，3 维单纯形是正四面体，4 维单纯形可能难以理解，但可以想象，它的表面是四面体……

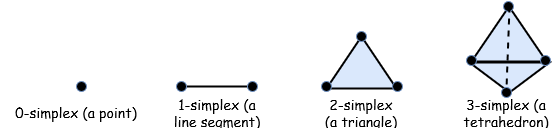
纯复形是由不同的单纯形 “粘合” 起来的。例如，我们可以用 1 维单纯形（线段）连接两个 2 维单纯形（三角形）。

例子（单纯复形）：

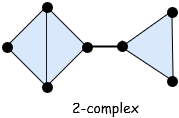
这是两个三角形沿着一条边连接，并和另一个三角形用 1 维单纯形（线段）连接。我们称之为 2 维单纯复形，因为组成这个复形的最高维单纯形是 2 维单纯形。

单纯形的表面是它的边界。如 1 为单纯形（线段）的表面是个点（0 维单纯形），2 维单纯形（三角形）的表面是线段，3 维单纯形（正四面体）的表面是三角形（2 维单纯形），以此类推。当描述单纯形或复形的时候，传统的在单纯形表面 “染色” 使它清楚地表明它是“固体”。例如，在画图时，我们将三个 1 维单纯形首尾相接它仍是 1 维单纯复形，尽管它看起来很像 2 维单纯形。如果我们在表面涂上色，那我们就可以确定它是一个被填充的 2 维单纯形。

单纯形 v.s 单纯复形。“涂色” 的重要性。

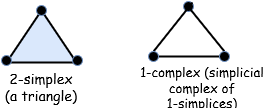
好的，我们对单纯形是什么有了一个直观的概念，但是现在我们需要一个精确的数学定义。

抽象单纯形： 一个抽象的单纯形是任何一个有限的顶点集合。例如，单纯形 \(J=\{a, b\}\) 和单纯形 \(K=\{a, b, c\}\) 分别代表了 1 维单纯形和 2 维单纯形。

知道了抽象单纯形的定义。抽象单纯形和抽象单纯复形都是抽象的，因为我们没有给他们任何具体的几何实现。它们是 “图形化” 的对象，因为我们从技术上可以用无数种方式绘制这个单纯形（比如，直线画成曲线）。例如，几何 2 维单纯形可以在 \(\mathbb R^2\) 上通过连接点 \(\{(0,0),(0,1),(1,1)\}\) 并填充中心而形成三角形。几何单纯形的定义可以是不同的 (而且更复杂)，因为它需要包含一些边界内的所有点。

单纯复形： 一个单纯复形 \(\mathcal {K}\) 是单纯形的集合，它满足以下条件：
1. \(\mathcal {K}\) 中任意一个单纯形的任意面仍属于 \(\mathcal {K}\)
2. \(\mathcal {K}\) 中任意两个单纯形 \(\sigma_1, \sigma_2\) 的交集是空集或者二者共享的面中的其中一个。

举个例子，这里有个带标签的单纯复形，我们需要用数学定义它。

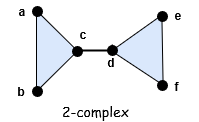
这个单纯复形被定义为一个集合: \(K=\{\{a\}, \{b\}, \{c\}, \{d\}, \{e\}, \{f\}, \{a, b\}, \{a, c\}, \{b, c\}, \{c, d\}, \{d, f\}, \{d, e\}, \{e, f\}, \{a, b, c\}, \{d, e, f\}\}\)。 注意，我们先列出了所有 0 维单纯形，然后再列出所有 1 维单纯形，然后再列出所有 2 维单纯形。如果还有任何更高维的单纯形，我们也需要以此法列出。所以我们满足第二个条件，因为所有高维单纯形的任何面都会先被列出直到列出所有顶点。当然，因为它是集合，顺序并不重要，然而，以这种方式列出是为了便于阅读。

单纯复形的第二个定义条件说明这样的结构不属于单纯形或者单纯复形：

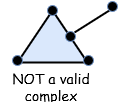
这是无效的，因为线段连接到三角形的边缘而不是它的顶点。

当我们分析数据，我们的数据通常以有限的度量空间的形式存在，例如，我们有一个定义的度量函数（它们在一些度量空间里，像欧几里得空间）的离散点（例如数据从数据的行和列中），这给了我们一个 “点云”。点云只是在我们的空间中放置的一系列点，没有明显的关系。

这个在 \(\mathbb R^2\) 中的点云看起来像一个圆，或者说这些点看起来好像是从一个圆中取样的。

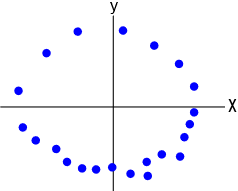
这是一组在 \(\mathbb R^2\) 中相似的点云，但它看起来比圆更小而且更椭圆。

几何学家从这两个点云中构建了单纯复形，他们会说它们的形状完全不同。但是，拓扑学家会说它们在拓扑上是完全相同的，因为它们都有一个 “循环” 特征，并且只有一组分量（“块”）。拓扑学家并不关心大小 / 规模的差异，也不关心边缘的扩展，他们关心拓扑的不变量(拓扑空间的性质不随特定类型的连续变形而变化)，例如孔、环和连接的组件。

那么我们如何从数据中构建一个单纯复形呢？我们如何计算这些拓扑不变量？ 实际上，有许多不同类型的单纯复形结构具有不同的属性。有些比较容易用数学描述，有些比较容易计算，有些简单但计算效率低。最常见的单纯复形的名字如切赫复形（Čech complex），维托里斯 - 里普斯复形（Vietoris–Rips complex），阿尔法复形（alpha complex），威特尼斯复形（witness complex）。

我们将关注一种，维托里斯 - 里普斯复形（VR complex，或简称为 VR 复形），因为从计算的角度来说，描述和实际操作是相当容易的。我也将简略地描述其他的复形。

构建 VR 复形

直观地讲，我们通过在 P 中最初的连结点的边缘低于一些互相ϵ任意定义的距离在点云 \(P \subseteq \mathbb R^d\) （ \(d\) - 维空间的子集 \(P\) ）中构建了 VR 复形。这将构建一个 1 维复形，如上所述 (顶点的集合和这些顶点之间的一组边)，它本质上是一个图。接下来，我们需要填充高维的单纯形，例如，任何三角形，四面体等，这样我们就不会有一堆空洞。

下面是在 \(\mathbb R^2\) 构建从圆形结构中取样的 VR 复形的可视化的主要步骤 (从左到右)：

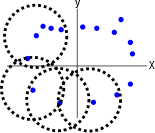
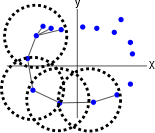
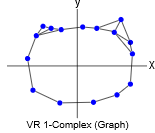
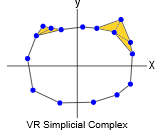
正如你所看到的，我们用叫做 \(\epsilon\) - 球（以 \(\epsilon\) 半径的虚线圆）去围绕 \(P\) 中的每一个点，并在这个点和它的圈内的所有其他点之间连线。我只在左边的几个点上画了几个点，因为如果我把它们都画出来，就很难看清了。一般地说，一个围绕 \(d\) 维空间点的球是 \((d-1)\) 维空间中围绕那个点的球（球指代空间中所有与某一点距离相同的点的集合）的泛化。所以 \(\mathbb R\) 中的球是一条围绕着某个点的线段， \(\mathbb R^2\) 中的球是圆， \(\mathbb R^3\) 中的球是球体，以此类推。重要的是要认识到一个 VR 结构不仅取决于点云数据，还取决于任意选择的参数 \(\epsilon\) 。

注解（如何选择 \(\epsilon\) ？）
所以如何选择 \(\epsilon\) ？这是一个好问题，并且答案也非常简单：你只需要选择多个不一样的ϵ然后看看在一个有意义的 VR 复形中它的结果。如果你设置的 \(\epsilon\) 太小，那么复形可能只包含原始的点云，或者仅仅是点之间的几个边。如果你设置的 \(\epsilon\) 太大，点云就会变成一个巨大的超维复形。我们稍后会学到，在单纯复形中发现一个真正有意义的模型的关键在于从 \(0\) 到一个使结果变成巨大单形的最大值不断改变参数 \(\epsilon\) （并不断重建复形）。这样，你就能生成一个随着 \(\epsilon\) 不断增大，拓扑模型特征从诞生到消亡的图像。我们假设随着 \(\epsilon\) 不断增大，能保持更长时间的特征是有用的特征，而寿命很短的特征更可能是噪声。这个过程称为持续同调，因为它发现了在你持续变化 \(\epsilon\) 时，拓扑空间中持续存在的同源特征。在我们学会如何从数据中构建单纯复形之后，我们将深入地研究持续同调。

让我们精确地定义 VR 结构……

VR 复形：如果在 d - 维空间中有一个点集 P， \(\mathbb R^d\) 的子集，那么比例 \(\epsilon\) 的 VR 复形 \(V_{\epsilon}(P)\) 是这样定义的： \(V_{\epsilon}(P) = \{ \sigma \subseteq P \mid d(u,v) \le \epsilon, \forall u \neq v \in \sigma \}\)

意思是：比例 \(\epsilon\) 下的 VR 复形是集合 \(V_{\epsilon}(P)\) 中的 \(P\) 的所有子集 \(\sigma\) ，也就是说 \(\sigma\) 中任何不同点之间的距离不大于参数 \(\epsilon\) 。

基本上，如果我们有包含一系列点的数据集 \(P\) ，如果 \(\sigma\) 的点在距离 \(\epsilon\) 之内，我们可以加入一个单纯形 \(\sigma\) （ \(P\) 的子集）。因此我们会得到集合 \(P\) 全是单纯形的子集，而 \(P\) 就是单纯复形。

预告

这章在这里就结束了，但我们将会在第 2 部分中讲到，我们将开始用代码来构建关于一些数据的 VR 复形。

参考文献（网站）

1. Applying Topology to Data, Part 1: A Brief Introduction to Abstract Simplicial and Čech Complexes.
2. http://www.math.uiuc.edu/~r-ash/Algebra/Chapter4.pdf
3. Group (mathematics)
4. Homology Theory — A Primer
5. http://suess.sdf-eu.org/website/lang/de/algtop/notes4.pdf
6. Evan Chen • Napkin

参考文献（学术刊物）

1. Basher, M. (2012). On the Folding of Finite Topological Space. International Mathematical Forum, 7(15), 745–752. Retrieved from http://www.m-hikari.com/imf/imf-2012/13-16-2012/basherIMF13-16-2012.pdf
2. Day, M. (2012). Notes on Cayley Graphs for Math 5123 Cayley graphs, 1–6.
3. Doktorova, M. (2012). CONSTRUCTING SIMPLICIAL COMPLEXES OVER by, (June).
4. Edelsbrunner, H. (2006). IV.1 Homology. Computational Topology, 81–87. Retrieved from Computational Topology
5. Erickson, J. (1908). Homology. Computational Topology, 1–11.
6. Evan Chen. (2016). An Infinitely Large Napkin.
7. Grigor’yan, A., Muranov, Y. V., & Yau, S. T. (2014). Graphs associated with simplicial complexes. Homology, Homotopy and Applications, 16(1), 295–311. HHA 16 (2014) No. 1 Article 16
8. Kaczynski, T., Mischaikow, K., & Mrozek, M. (2003). Computing homology. Homology, Homotopy and Applications, 5(2), 233–256. HHA 5 (2003) No. 2 Article 8
9. Kerber, M. (2016). Persistent Homology – State of the art and challenges 1 Motivation for multi-scale topology. Internat. Math. Nachrichten Nr, 231(231), 15–33.
10. Khoury, M. (n.d.). Lecture 6 : Introduction to Simplicial Homology Topics in Computational Topology : An Algorithmic View, 1–6.
11. Kraft, R. (2016). Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology.
12. Lakshmivarahan, S., & Sivakumar, L. (2016). Cayley Graphs, (1), 1–9.
13. Liu, X., Xie, Z., & Yi, D. (2012). A fast algorithm for constructing topological structure in large data. Homology, Homotopy and Applications, 14(1), 221–238. HHA 14 (2012) No. 1 Article 11
14. Naik, V. (2006). Group theory : a first journey, 1–21.
15. Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. (2015). A roadmap for the computation of persistent homology. Preprint ArXiv, (June), 17. Retrieved from [1506.08903] A roadmap for the computation of persistent homology
16. Semester, A. (2017). § 4 . Simplicial Complexes and Simplicial Homology, 1–13.
17. Singh, G. (2007). Algorithms for Topological Analysis of Data, (November).
18. Zomorodian, A. (2009). Computational Topology Notes. Advances in Discrete and Computational Geometry, 2, 109–143. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.50.7483
19. Zomorodian, A. (2010). Fast construction of the Vietoris-Rips complex. Computers and Graphics (Pergamon), 34(3), 263–271. Redirecting
20. Symmetry and Group Theory 1. (2016), 1–18. Redirecting